Миноры и их алгебраические дополнения. Теорема лапласа.

Пусть В — некоторая матрица размером n x n. В = ,и kÎN,

1 ≤ k ≤ n.

Выделим в матрице В k произвольных строк с номерами i₁, i₂,..., i_k и k произвольных столбцов с номерами j_1, j₂,..., j_k. Элементы, стоящие на пересечении этих строк и столбцов, образуют матрицу размером k x k. Определитель полученной матрицы называется минором к -того порядка матрицы В. Обозначим его через М. Элементы, не попавшие на пересечение, образуют матрицу размером (n-k) x (n-k). Определитель полученной матрицы называют минором, дополнительным к минору М. Обозначим его через М₁.

Введем еще следующую сумму: S_M = i₁+ i₂+...+i_k + j₁+ j₂+...+j_k. Сумма S_M — это сумма номеров выделенных строк и выделенных столбцов. Тогда

М₁= А_m называется алгебраическим дополнением к минору М.

Существует общий способ сведения вычисления определителей порядка n к вычислению определителей меньших порядков с применением понятия минора и алгебраического дополнения.

Теорема Лапласа.

Пусть В Î Р(n x n) — матрица порядка n, и 1 ≤ k < n. У матрицы В зафиксируем k произвольных строк. Тогда ее определитель равен сумме произведений всех миноров, содержащихся в выделенных строках, на их алгебраические дополнения, т.е. | B | = M1A1 +... + MsAs.

СЛЕДСТВИЕ 1, 2 ИЗ ТЕОРЕМЫ ЛАПЛАСА

Следствие 1 (разложение определителя по строке). Определитель матрицы В равен сумме произведений элементов какой–нибудь строки на их алгебраические дополнения.

< Следует из теоремы Лапласа при k = 1. >

Следствие 1 позволяет сводить вычисление определителя порядка n к вычислению определителей порядка (n - 1).

Следствие 2. Сумма произведений элементов строки определителя матрицы B на соответствующие дополнения к элементам другой строки равна нулю, т.е..

Пример:

 

det = det * det * (-1)(^1+2+1+2) =

=det * det = (-2) * (-3) = 6.

 

ОПРЕДЕЛИТЕЛЬ ПРОИЗВЕДЕНИЯ МАТРИЦ.

Теорема. Пусть А и В — две квадратные матрицы порядка n. Тогда определитель их произведения равен произведению определителей, т.е.

| AB | = | A| | B |.

< Пусть A = (aij) (n x n), B = (bij) (n x n). Рассмотрим определитель (d) (2n) порядка 2n

A

||

(d) (2n) =

||

B

 

(d) (2n) = | A | | B | (-1)(^1+...+n+1+...+n) = | A | | B |.

Если мы покажем, что определитель (d) (2n) равен определителю матрицы С=АВ, то теорема будет доказана.

В (d) (2n) проделаем следующие преобразования: к 1 строке прибавим (n+1) строку, умноженную на а11; (n+2) строку, умноженную на а12 и т.д. (2n) строку, умноженную на (а) (1n). В полученном определителе первые n элементов первой строки будут нулями, а n других элементов станут такими:

a11* b11 + a12 * b21 +... + (а) (1n) * (d) (1n) = c11_;

a11* b12 + a12 * b21 +... + (а) (1n) * (d) (2n) = c12_;

_...

a11* (d) (1n) + a12 * (d) (2n) +... + (а) (1n) * (d) (nn) = (c) (1n)_.

Аналогично получаем нули во 2, …, n строках определителя (d) (2n), причем последние n элементов в каждой из этих строк станут соответствующими элементами матрицы С. В результате, определитель (d) (2n) преобразуется в равный ему определитель:

 

 

(d) (2n) = | C | (-1))(^1+...+n+...+2n) = |AB|. >

Следствие. Определитель произведения конечного числа квадратных матриц равен произведению их определителей.

< Доказательство проводится индукцией: | A1... (A) (j+1) | = | A1... Aj | | (A) (j+1) | =... = | A₁|... | A_i+1 |. Эта цепочка равенств верна по теореме.>

 

ОБРАТНАЯ МАТРИЦА.

Пусть A = (aij) (n x n) квадратная матрица над полем Р.

Определение 1. Матрицу А будем называть вырожденной, если ее определитель равен 0. Матрицу А будем называть невырожденной в противном случае.

Определение 2. Пусть А Î Pn. Матрицу В Î Pn будем называть обратной к А, если АВ = ВА=Е.

Теорема (критерий обратимости матрицы).Матрица А обратима тогда и только тогда, когда она невырожденная.

< Пусть А имеет обратную матрицу. Тогда АА(^-1) = Е и, применяя теорему об умножении определителей, получаем | A | | A(^-1) | = | E | или | A | | A(^-1) | = 1. Следовательно, | A | ¹ 0.

Пусть, обратно, | A | ¹ 0. Надо показать, что существует матрица В такая, что АВ = ВА = Е. В качестве В возьмем такую матрицу:

В = ,

где А_ij — алгебраическое дополнение к элементу а_ij. Тогда

 

 

АВ =

Следует заметить, что в результате получится единичная матрица (достаточно воспользоваться следствиями 1 и 2 из теоремы Лапласа), т.е. АВ = Е. Аналогично показывается, что ВА = Е. >

Пример. Для матрицы А найти обратную матрицу, или доказать, что ее нет.

 

 

А =

det A = -3 Þ обратная матрица существует. Теперь считаем алгебраические дополнения.

А₁₁ = -3 А₂₁ = 0 А₃₁ = 6

А₁₂ = 0 А₂₂ = 0 А₃₂=-3

А₁₃ = 1 А₂₃ = -1 А₃₃ = -1

 

Итак, обратная матрица имеет вид: В = =

Алгоритм нахождения обратной матрицы для матрицы

1. Вычисляем det A.

2. Если он равен 0, то обратной матрицы не существует. Если det A не равен

0, считаем алгебраические дополнения.

3. Ставим алгебраические дополнения на соответствующие места.

4. Все элементы получившейся матрицы делим на det A.

 

???. СИСТЕМЫ ЛИНЕЙНЫХ УРАВНЕНИЙ.

Определение 1. Уравнение вида a1x1+....+an xn=b, где a,...,an — числа; x1,...,xn — неизвестные, называется линейным уравнением с n неизвестными.

s уравнений с n неизвестными называется системой s линейных уравнений с n неизвестными, т.е.

(1)
Матрица А, составленная из коэффициентов при неизвестных системы (1), называется матрицей системы (1). .

 

Если к матрице А добавить столбец свободных членов, то получим расширенную матрицу системы (1).

X = — столбец неизвестных. — столбец свободных членов.

В матричном виде система имеет вид: AX=B (2).

Решением системы (1) называют упорядоченный набор n чисел (α1,…, αn) таких, что если сделаем подстановку в (1) x1 = α1, x2 = α2,…, xn = αn, то мы получим числовые тождества.

Определение 2. Систему (1) называют совместной, если она имеет решения, и несовместной в противном случае.

Определение 3. Две системы называют эквивалентными, если множества их решений совпадают.

Существует универсальный способ решения системы (1) — метод Гаусса (метод последовательного исключения неизвестных)

Рассмотрим более подробно случай, когда s = n. Существует метод Крамера решения таких систем.

 

 

Пусть d = det ,

dj — определитель d, в котором j–тый столбец заменен столбцом свободных членов.

 

ПРАВИЛО КРАМЕРА

Теорема (правило Крамера). Если определитель системы d ¹ 0, тогда система имеет единственное решение, получающееся по формулам:

x1 = d1 / d …xn = dn / d

<Идея доказательства заключается в том, чтобы переписать систему (1) в форме матричного уравнения. Положим

X = , B =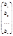

и рассмотрим уравнение AX = B (2) с неизвестной матрицей-столбцом X. Так как A, X, B — матрицы размеров n x n, n x 1, n x 1 соответственно, то произведение прямоугольных матриц АХ определено и имеет те же размеры, что и матрица В. Таким образом, уравнение (2) имеет смысл.

Связь между системой (1) и уравнением (2) заключается в том, что является решением данной системы тогда и только тогда, когда

столбец есть решение уравнения (2).

Действительно, это утверждение означает выполнение равенства

=

= .

Последнее равенство, как равенство матриц, равносильно системе равенств

которое означает, что — решение системы (1).

Итак, решение системы (1) сводится к решению матричного уравнения (2). Так как определитель d матрицы А отличен от нуля, она имеет обратную матрицу А^-1. Тогда АХ = В Þ А(^-1)(АХ) = А(^-1)В Þ (А(^-1)А)Х = А(^-1)В Þ ЕХ = А(^-1)В Þ Х = А(^-1)В (3). Следовательно, если уравнение (2) имеет решение, то оно задается формулой (3). С другой стороны, А(А(^-1)В) = (А А(^-1))В = ЕВ = В.

Поэтому Х = А(^-1)В есть единственное решение уравнения (2).

 

Так как ,

 

где А_ij — алгебраическое дополнение элемента a_ij в определителе d, то

 

= ,

 

 

откуда (4).

В равенстве (4) в скобках написано разложение по элементам j-го столбца определителя dj, который получается из определителя d после замены в нем

j-го столбца столбцом свободных членов. Поэтому, xj = dj/ d. >

Следствие. Если однородная система n линейных уравнений от n неизвестных имеет ненулевое решение, то определитель этой системы равен нулю.

 

⇐ Предыдущая1234567Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: