 |
Тригонометрическая форма комплексного числа.
|
|
|
|
Пусть z = a+bi, полагаем r =(def) 
=|z|, r — модуль комплексного числа z.
a+bi= 
, положим
= cos 
и 
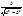= sin .
Пусть z¹0, тогда угол j определен однозначно с точностью до 2pk. Если 0£j£2p, то он определен однозначно. Угол j называют аргументом комплексного числа z, r и j — полярные координаты точки.
Из тригонометрии мы знаем как искать j, если известно a и b.
Если r=0, то j может быть любой, то есть аргумент нуля не определён; r¹0, то аргумент определен с точностью до 2πk.
z = r(cosj+i sinj) (1)
Назовем выражение (1) тригонометрической формой комплексного числа.
Если два комплексных числа равны, то их модули равны, а их аргументы, вообще говоря, отличаются на 2pk.
Теорема 1.
Пусть z1 = r1 (cosj1+i sinj1), z2 = r2 (cosj2+i sinj2). Тогда:
1) z1z2 = r1r2(cos(j1+j2)+i sin(j1+j2))
(модуль произведения комплексных чисел равен произведению модулей, а аргумент – сумме аргументов);
2) 
(модуль частного комплексных чисел равен частному модулей, а аргумент – разности аргументов).
Доказательство:
Докажем 1).
z1z2 =r1r2(cosj1cosj2–sinj1sinj2+i(sinj1cosj2+cosj1sinj2))=r1r2cos(j1+j2)+i sin(j1+j2)).
Аналогично с частным.
Следствие 1
Пусть z = r (cosj+i sinj), тогда z^(-1)= 
(cos(–j)+i sin(–j)).
Доказательство:
Z^(-1)= 
= 
= 
= 
(cos(–j)+i sin(–j)).
Следствие 2(формула Муавра).
Пусть z = r (cosj+i sinj). Тогда z^n= r^n(cos(nj)+i sin(nj)) для любого nÎZ.
Доказательство:
Если n — натуральное, то формула Муавра следует из правила умножения комплексных чисел в тригонометрической форме.
Если n — отрицательное, то можно представить z^n= (z -1)^(-n) и применить следствие (1) и доказанную формулу Муавра для nÎN.
Замечание.Тригонометрическая форма комплексного числа хорошо приспособлена для выполнения действий умножения, деления, возведения в степень.
ИЗВЛЕЧЕНИЕ КОРНЯ ИЗ КОМПЛЕКСНОГО ЧИСЛА.
|
|
|
Пусть z = a+bi.
Надо извлечь корень из z.
—?
обозначим через z1, то z1(^2)= z.
Пусть z1 = x+iy, тогда
(x2–y2)+2xyi = a+bi,
Решив эту систему, мы найдем подходящие значения z1.
Если так действовать и для извлечения корней более высокой степени, то придётся уметь решать уравнения соответствующих степеней.
Для извлечения корня из комплексного числа хорошо приспособлена тригонометрическая форма комплексного числа.
Пусть z = r(cosj+i sinj), надо найти 
= z1, положим
z1=ρ (cosy+i siny), z1(^n)==ρn(cos(ny)+i sin(ny), r = ρn Þ ρ = 
, j = ny+2pk Þy = 
.
Получим
= 
(cos 
+ i sin ) (1),
где k — любое целое число, то есть корень n–той степени из произвольного комплексного числа z всегда существует и его можно посчитать по формуле (1), причем формула (1) даёт все корни, если k пробегает множество целых чисел (достаточно ограничиться k = 0,…, n–1)
Если возьмем k – любое, то мы можем разделить его с остатком на n:
k = nq+s; 0£s£n–1
.
Углы [2] и [3] отличаются на кратное 2p, и поэтому косинусы и синусы от них совпадают, следовательно формула (1) при угле [2] и при угле [3] даёт одинаковое значение.
Если брать k от 0 до n–1, то мы получим все значения. Нетрудно заметить, что все эти значения разные (смотри геометрическую интерпретацию).
Теорема 4.
Извлечение корня степени n из комплексного числа всегда возможно, и даёт n различных значений, получающихся по формуле (1).
Теорема нами доказана ранее.
Замечание(геометрическая интерпретация).
Все значения 
расположены на окружности радиуса 
с центром в начале координат и делят окружность на n равных частей:
КОРНИ ИЗ ЕДИНИЦЫ.
1=cos0+isin0 Þ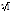 
=cos 
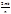+isin 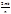, k=0,1,…,n-1.
Корни расположены на окружности единичного радиуса и делят эту окружность на n равных частей.
Теорема 1.
Все значения корня n–той степени из комплексного числа z можно получить умножением одного из них на все корни из 1.
Доказательство:
Возьмём a = 
= 
(cos 
+i sin 
), где s–фиксированное число.
|
|
|
e1, e2,…, en – так обозначим все корни 
.
Домножим каждый из корней e1,…, en на a. Они разные, все являются корнями n–той степени из z, ибо (aei)n = z и их n штук.
Теорема доказана.
Теорема 2.
Произведение двух корней n–той степени из единицы есть корень степени n из единицы.
Следствие.
Степень корня n–той степени из единицы есть корень степени n из единицы.
Все ли корни из 1 равноправны?
n=4; 1, –1, i, –i — корни из единицы.
i; –i — первообразные корни; если i возводить в степени 0, 1, 2, 3, то получим все корни.
Определение 1.
Корень n–той степени из 1 называется первообразным, если он не даёт единицу в степени меньше, чем n.
Всегда ли есть первообразный корень?
Всегда! Например: cos 
+i sin .
Упражнение. Доказать, что корень n–той степени
ek = cos 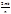+ i sin 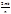будет первообразным, если n и k — взаимно простые (не имеют общих делителей отличных от 1)
ЧИСЛОВОЕ ПОЛЕ.
В множествах Q Ì R Ì C возможны четыре операции +, -, *, /.
Определение 1. Подмножество K Ì C множества комплексных чисел C, состоящее более, чем из одного элемента, называют числовым полем, если выполняются следующие условия:
1) " a, bÎK Þ a+bÎK, то есть в множестве K всегда возможно сложение;
2) " aÎK Þ –aÎK;
3) " a, bÎK Þ abÎK, то есть задано умножение в K (K замкнуто относительно умножения);
4) " a ¹ 0; a(^-1)ÎK.
Из 2) с учётом 1) получаем, что в K всегда возможно вычитание.
Из 4) с учётом 3) получаем, что в K всегда возможно деление на число не равное 0.
Q — поле рациональных чисел;
R — поле вещественных чисел;
C — поле комплексных чисел.
Упражнение 1.Числовое поле всегда бесконечно.
Упражнение 2. Любое числовое поле всегда содержит Q (множество рациональных чисел).
Пример поля отличного от Q, R и C:
K = {a+b 
, где a и b ÎQ }.
|
|
|
