Умножение матриц. Ассоциативность умножения.

Мы никак не мотивировали операцию сложения матриц, но едва ли это вызвало недоумение в силу своей естественности. Операция умножения матриц уже не обладает этим качеством.

Пусть A = (aij) (n x m), B = (bij) (n x p). Под произведением АВ понимают матрицу С с элементами cij

cij =

АВ:= С= (сij) (m x p).

Например, А = и В = .

 

Тогда AВ =

 

5=1*0 + 2*1 + 3*1

6=1*1 + 2*1 + 3*1

7= 1*4 + 2*0 + 3*1 и т.д.

 

Берется i-тая строка матрицы А и j-тый столбец матрицы В, перемножаются покомпонентно и результаты складываются. Это есть элемент матрицы С на позиции i,j.

Свойство. Произведение матриц не коммутативно, т.е. АВ¹ВА, в том числе и квадратных.

Пример (доказывающий свойство):

=

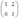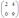
Замечание 1. Запись A = (aij) (n x m) обозначает, что матрица А имеет размеры

m x n.

Замечание 2. В двойной сумме результат суммирования не зависит от порядка суммирования, т.е.

, ибо левая часть равенства и правая часть есть сумма элементов матрицы .

Теорема (об ассоциативности произведения матриц).все но

Пусть А, В, С — матрицы над числовым полем Р такие, что определено произведение АВ и ВС. Тогда имеют смысл произведения (АВ)С, А(ВС) и верно равенство (АВ)С = А(ВС).

< Пусть A = (aij) (n x m), B = (bij) (n x p), C=(cij) (p x s). Они подходящих размеров, чтобы было определено AB и BC. Введем обозначения АВ =(dij) (m x p), BC = (lij) (n x s), A(BC) =(fij) (m x s), (AB)C = (rij) (m x s). Матрицы A(BC) и (AB)C одинаковых размеров. Требуется проверить, что fij = rij. Выразим fij и rij через элементы матриц А, В, С:

 

fij= = =

.

 

Полученные суммы отличаются лишь порядком суммирования, что не влияет на результат (по замечанию 2). >

Определение. Произведение нескольких матриц определим индуктивно, т.е. если имеем k матриц, то их произведение определим следующим образом: (A1,..., A(k-1)) Ak

Упражнение. Доказать, что в произведении нескольких матриц скобки можно расставлять как угодно.

Указание. Воспользоваться ассоциативностью.

Теорема 2. Пусть A = (aij) (n x m). Тогда AEn = EmA = A, где Е — единичная матрица подходящего размера.

< Доказательство проводится непосредственной проверкой равенства:

=

Аналогично доказывается, что E_mA = А.>

Теорема 3. Пусть A = (aij) (n x m). Тогда АО (n x s) = O (m x s), где О — нулевая матрица подходящего размера.

< Произведение таких матриц будет матрицей размером m x s. Каждый элемент, очевидно, будет равен 0. >

Теорема 4. (дистрибутивность умножения матриц относительно сложения матриц).

(А + В)С = АС + ВС, где С — матрица подходящего размера, A и B — матрицы одинаковых размеров.

< Пусть A = (aij) (n x m), B = (bij) (m x n), C=(cij) (n x p). Понятно, что (А + В)С и АС + ВС одинаковых размеров. Чтобы доказать их равенство, надо показать, что на одних и тех же местах стоят одни и те же элементы.

Следующее равенство доказывает теорему:

 

элемент на элемент элемент на

позиции I,j на позиции позиции I,j

матрицы I,j матрицы матрицы

(A + B)C AC AB

 

 

ТРАНСПОНИРОВАНИЕ МАТРИЦ.

Определение 1. Пусть A = (aij) (n x m). Транспонирование матрицы — это такое ее преобразование, при котором строка с номером i записывается в столбец с тем же номером.

Обозначение: А^t, А^tr, А'.

Пример:

, то .

Теорема 5. Имеют место следующие равенства:

1. (А^t)^t = A.

2. (αA + βB)^t = αA^t + βB^t.

3. (AB)^t = В^tА^t .

Причем, А и В — матрицы подходящих размеров, α и β — любые числа.

< 1. А = (а_ij)_{m x n}

(A)^t = (а_ji)_{n x m} Þ (А^t)^t = A.

3. Пусть имеем А = (а_ij)_{m x n} и B = (b_ij)_{n x s}. Тогда A(^t) = ( ij) (m x n), B (^t)=( ij) (s x m), AB = (cij) (m x s), (BА)(^t) = (dij)(s x m)

Матрица В(^t)A(^t) и AB)(^t)одинаковых размеров, и чтобы доказать, что В(^t)A(^t) = (AB)(^t), надо показать, что на одинаковых местах стоят одинаковые элементы.

Мы получили, что на позиции ij у матрицы В(^t)A(^t) и матрицы AB)(^t) стоит один и тот же элемент. >

Определение 2. Матрица А называется симметрической, если A(^t) = А, и кососимметрической, если A(^t) = -А.

Пример. Симметрическая матрица:

 

кососимметрическая матрица:

 

ПЕРЕСТАНОВКИ.

Пусть X — непустое множество элементов произвольной природы, так как природа элементов для нас несущественна, то в случае конечного множества считаем X ={1,2,3,…,n}

Определение 1. Любое упорядоченное расположение элементов множества X называется перестановкой множества X.

Пример:

Если X ={1,2,3,4,5}, то (2,5,3,4,1) - перестановка множества X.

Перестановку элементов множества X обозначают(a1,a2,…,an), причем среди ai (i = 1,2,…, n) нет равных.

Определение 2. Две перестановки множества X называются равными, если у них на одинаковых местах стоят одинаковые элементы.

Теорема 1.Число различных перестановок множества из n элементов равно n!

< Докажем эту теорему индукцией по числу n. При n=1 имеется одна перестановка, т.е. 1!.

Пусть n>1 и число различных перестановок, которые можно составить из заданных (n-1) элементов, равно (n-1)!. Всякая перестановка данных элементов с фиксированным первым числом а имеет вид:

a1,a2,…,an.

где a2,…,an произвольная перестановка оставшихся (n-1) элементов. По индуктивному предположению число таких перестановок равно (n-1)!. В качестве а, можно взять любой из данных n элементов, поэтому число различных перестановок заданных n элементов равно сумме n слагаемых, каждое из которых есть(n-1)!, т.е. n! >

Определение 3. Будем говорить, что в перестановке чисел (a1,a2,…,an) два числа ai,aj образуют инверсию если ai>aj, но i < j. В противном случае ai,aj образуют порядок.

Пример:

В перестановке (1 3 4 2) инверсии: 4,2; 3,2, а остальные пары образуют порядок.

Определение 4. Количество пар чисел, образующих инверсию в перестановке, называют числом инверсий данной перестановки. Отображение X®X будем называть преобразованием множества X.

Пусть множество X состоит не менее чем из двух элементов a,bÎX.

Определение 5. Преобразование множества Х называют транспозицией элементов a и b, если , , " x¹a,b.Такое преобразование обозначают (a,b).

Определение 6. Перестановку называют четной, если число инверсий в ней четно, и нечетной в противном случае.

Теорема 2.Однократное применение транспозиции к перестановке изменяет ее характер четности на противоположный.

< Пусть имеется перестановка (a1,…,a,…,b,…an) (1). Применим к ней транспозицию(a,b), получим(a1,…,b,…,a,…an) (2). Рассмотрим несколько случаев:

1. Пусть a и b стоят рядом. Если a и b в (1) образуют инверсию, то (2) образуют порядок. Поэтому характер четности изменяется на противоположный, ибо число инверсий изменяется на единицу.

2. Пусть a и b не стоят рядом (a1,…,a,…,b,…an). От (1) к (2) можно перейти следующим способом: a менять с рядом стоящим элементом дойти до b и b перегнать на место a. Всего нам придется применить S+1+S=2S+1 транспозиций соседних чисел, где S число элементов между a и b, поэтому характер четности перестановок (1) и (2) различны.>

Следствие. При n³2 число четных перестановок равно числу нечетных перестановок и равно n!/2.

< Пусть число четных перестановок равно S, нечетных — T. Если к каждой четной перестановке мы применим транспозицию двух элементов, мы превратим их в нечетные S£T, аналогично наоборот T £S Þ T=S

n!=S+T =2S

S=T=n!/2. >

Теорема 3.Пусть даны две различные перестановки одних и тех же чисел, тогда существует последовательность транспозиций переводящих первую перестановку во вторую.

< Пусть (a1,a2,…,an) (3) (b1,b2,…,bn) (4)

есть произвольные перестановки из n чисел. Если a1¹a2, то применив к перестановке (3) транспозицию (a1,b2) получим перестановку n чисел вида

(b1,l2,l3,…,ln) (5)

Если l2¹b2, то к перестановке (5) применим транспозицию (l2,b2).В результате получим перестановку (b1,b2,r3,…rn). Продолжаем этот процесс получаем требуемое.>

 

ПОДСТАНОВКИ.

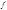Пусть X®X, при этом если — биективно, то часто 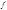называют подстановкой. Мы ограничимся случаем, когда число элементов конечно, и равно n.

X ={1,2,3,…,n}, тогда отображение можно записать в виде таблицы:

 

(1)

 

Если подстановка, тогда — перестановка. Запись отображения в виде таблице (1) позволяет хорошо перемножать отображения.

Пример.

 

Теорема 1. Всякая подстановка конечного множества, содержащая не менее двух элементов, может быть представлена в виде произведения транспозиций.

< Пусть имеем = .Согласно теореме 3 предыдущего параграфа, существует последовательность транспозиций переводящая первую перестановку во вторую, пусть это будет следующая последовательность транспозиций t1,t2,…,tn. Тогда очевидно, что , ибо отображения действуют на одном и том же множестве и результат их действия одинаков. >

Замечание. Разложение подстановки в произведение транспозиций, вообще говоря, неоднозначно.

Теорема 2. Характер четности числа сомножителей во всех разложениях подстановки в произведение транспозиций один и тот же.

 

◄ Пусть подстановка вида (1) разлагается в произведение k транспозиций. Это значит, что существует последовательность k транспозиций, переводящая перестановку (1,2,…,n) (2) в перестановку 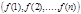(3). Однократное применение транспозиции меняет характер четности перестановки, поэтому k — четное число тогда и только тогда, когда перестановки(2) и (3) одного характера четности. Это и доказывает теорему. >

Определение 1. Подстановка называется четной, если она разлагается в произведение четного числа транспозиций, и нечетная в противном случае.

Упражнение. Число четных подстановок равно числу нечетных и равно n!/2.

 

⇐ Предыдущая1234567Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: