 |
Схема расчета скользящих средних для периода осреднения равного четырем (ежеквартальные данные за несколько лет) представлена в таблице 1.
|
|
|
|
Таблица 1.
| номер перио-да t | фактические значения ряда 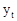
| межинтервальные скользящие средние ССt | интервальные (центрированные) скользящие средние ЦССt | |
 1 1
| 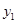
| |||
 2 2
| 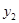
| |||

| ||||
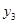
| 
| |||

| ||||

| 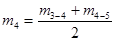
| |||

| ||||

| 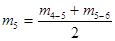
| |||

| ||||

| ||||
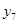
| ||||
Дальнейшая схема определения сезонных колебаний различна для аддитивной и мультипликативной моделей, по этому рассмотрим их по отдельности.
Аддитивная модель
Вначале находят для каждой точки временного ряда сезонные отклонения от предполагаемой тенденции, для этого:
- находятся скользящие средние с периодом усреднения равным L;
- в случае если период сезонных колебаний представляет собой четное число, то полученные скользящие средние являются межинтервальными и для получения центрированных скользящих средних осуществляется усреднение полученных средних еще раз, но на этот раз с периодом усреднения равным двум;
- для каждого интервала времени находят сезонное отклонение СКt как разность между фактическими значениями и соответствующими средними, т.е.:
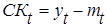 .
.
Полученные сезонные отклонения являются базой для вычисления нормированных сезонных составляющих Sl для каждого интервала из периода сезонных колебаний L. Для этого полученные отклонения 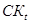 группируются по одинаковым номерам точек в периоде сезонных колебаний и в каждой из полученных L групп находятся средние значения сезонных отклонений
группируются по одинаковым номерам точек в периоде сезонных колебаний и в каждой из полученных L групп находятся средние значения сезонных отклонений  . Для того чтобы сезонные составляющие не приводили к искажению тенденции при их исключении из исходного временного ряда необходимо, чтобы выполнялось условие:
. Для того чтобы сезонные составляющие не приводили к искажению тенденции при их исключении из исходного временного ряда необходимо, чтобы выполнялось условие:
|
|
|
 .
.
Как правило, это условие никогда не выполняется, по этому вводится поправочный коэффициент k, равный:
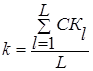 ;
;
Сезонная составляющая для каждой точки периода сезонных колебаний с учетом поправочного коэффициента будет равна:

В таблицах 2 - 3 приведен пример иллюстрирующий определение сезонной составляющей по аддитивной модели.
Таблица 2. Расчет сезонных отклонений от тенденции.
| N | Y(t) | Скользящая средняя, L=4 | Центрирован-ная скользящая средняя | Сезонные отклонения | L |
| 6.0 | |||||
| 4.4 | |||||
| 5.0 | 6.10 | 6.250 | -1.250 | ||
| 9.0 | 6.40 | 6.450 | 2.550 | ||
| 7.2 | 6.50 | 6.625 | 0.575 | ||
| 4.8 | 6.75 | 6.875 | -2.075 | ||
| 6.0 | 7.00 | 7.100 | -1.100 | ||
| 10.0 | 7.20 | 7.300 | 2.700 | ||
| 8.0 | 7.40 | 7.450 | 0.550 | ||
| 5.6 | 7.50 | 7.625 | -2.025 | ||
| 6.4 | 7.75 | 7.875 | -1.475 | ||
| 11.0 | 8.00 | 8.125 | 2.875 | ||
| 9.0 | 8.25 | 8.325 | 0.675 | ||
| 6.6 | 8.40 | 8.375 | -1.775 | ||
| 7.0 | 8.35 | ||||
| 10.8 |
Таблица 3. Расчет сезонной составляющей.
| Показатель | Номер квартала l | ||||
| 1 год | - | - | -1.250 | 2.550 | |
| 2 год | 0.575 | -2.075 | -1.100 | 2.700 | |
| 3 год | 0.550 | -2.025 | -1.475 | 2.875 | |
| 4 год | 0.675 | -1.775 | - | - | |
| Среднее сезонное отклонение | 0.600 | -1.958 | -1.275 | 2.708 | |
| Сумма средних сезонных отклонений | 0.075 | ||||
| Корректирующий коэффициент k | 0.075 / 4 = 0.01875 | ||||
| Сезонная составляющая | 0.581 | -1.977 | -1.275 | 2.708 | |
Для вычленения сезонной составляющей из исходного ряда yt необходимо вычесть из каждой точки этого ряда соответствующую сезонную компоненту, т.е. найти разность 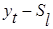 которая будет представлять собой сумму тенденции и свободного члена
которая будет представлять собой сумму тенденции и свободного члена  . Полученный таким образом временной ряд без сезонных колебаний используется для нахождения уравнения описывающего тенденцию.
. Полученный таким образом временной ряд без сезонных колебаний используется для нахождения уравнения описывающего тенденцию.
Мультипликативная модель
Методика определения сезонной составляющей (применительно к мультипликативной модели ее часто называют индексом сезонности) во многом схожа с аддитивной моделью. Также как и в предыдущем случае определяются центрированные скользящие средние и с их помощью находятся сезонные отклонения. Но в отличии от аддитивной модели сезонные отклонения определяются как частное от деления фактических значений ряда 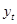 на соответствующие скользящие средние. Второе отличие заключается в нахождении по полученным средним сезонным отклонениям
на соответствующие скользящие средние. Второе отличие заключается в нахождении по полученным средним сезонным отклонениям  сезонных составляющих
сезонных составляющих  . Для предотвращения искажений тенденции при вычленении сезонных колебаний из исходного ряда необходимо, чтобы сумма сезонных компонент была равна периоду сезонных колебаний, т.е. выполнялось условие:
. Для предотвращения искажений тенденции при вычленении сезонных колебаний из исходного ряда необходимо, чтобы сумма сезонных компонент была равна периоду сезонных колебаний, т.е. выполнялось условие:  .
.
|
|
|
В случае его невыполнения вводится поправочный коэффициент k определяемый по формуле:
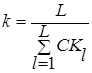
Сезонные составляющие определяются как произведения соответствующих средних сезонных отклонений на поправочный коэффициент: 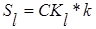 .
.
Пример расчета сезонных составляющих для мультипликативной модели приведен в таблицах 4 – 5.
Таблица 4. Расчет сезонных отклонений 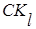 .
.
| N | Y(t) | Скользящая средняя, L=4 | Центрированная скользя-щая средняя | Сезонные колебания | L |
| 81.5 | 81.25 | 1.108 | |||
| 81.0 | 80.00 | 0.800 | |||
| 79.0 | 77.75 | 0.900 | |||
| 76.5 | 75.75 | 1.215 | |||
| 75.0 | 74.00 | 1.081 | |||
| 73.0 | 71.50 | 0.811 | |||
| 70.0 | 68.50 | 0.905 | |||
| 67.0 | 65.75 | 1.217 | |||
| 64.5 | 63.25 | 1.075 | |||
| 62.0 | 59.5 | 0.807 | |||
| 57.0 | 54.75 | 0.950 | |||
| 52.5 | 50.25 | 1.194 | |||
| 48.0 | |||||
Таблица 5. Расчет сезонной составляющей 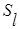 .
.
| Показатель | Год | Номер квартала l | ||||||
| - | - | 1.108 | 0.800 | |||||
| 0.900 | 1.215 | 1.081 | 0.817 | |||||
| 0.905 | 1.217 | 1.075 | 0.807 | |||||
| 0.950 | 1.194 | - | - | |||||
| Среднее сезонное отклонение | 0.918 | 1.209 | 1.088 | 0.808 | ||||
| Сумма средних сезонных отклонений | 4.023 | |||||||
| Корректирующий коэффициент k | 4 / 4.023= 0.9943 | |||||||
| Сезонная составляющая | 0.913 | 1.202 | 1.082 | 0.803 | ||||
Для вычленения сезонной составляющей из исходного ряда 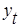 необходимо каждую его точку разделить на соответствующую сезонную компоненту, т.е. найти частное
необходимо каждую его точку разделить на соответствующую сезонную компоненту, т.е. найти частное 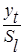 которая будет представлять собой произведение тенденции и свободного члена
которая будет представлять собой произведение тенденции и свободного члена  . Полученный таким образом временной ряд без сезонных колебаний используется для нахождения уравнения описывающего тенденцию.
. Полученный таким образом временной ряд без сезонных колебаний используется для нахождения уравнения описывающего тенденцию.
|
|
|
|
|
|


