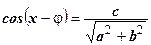|
и уравнений, приводимых к ним
|
|
|
|
и уравнений, приводимых к ним


Уравнение вида asinx+bcosx=c, a2+b2≠ 0
| 1) А это уже однородное тригонометрическое уравнение второй степени относительно | |
| 2) а) б) ОДЗ уравнения б) уже, чем ОДЗ уравнения а). Поэтому необходимо проверять, не являются ли числа | |
| 3) Тогда
| |
| Решений нет |  , ,  . Если . Если  , ,  , то , то
 находится из условия находится из условия  или или  Если
Если  , то , то  Если
Если 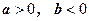 , то , то 
|
Задание 4: Решить тригонометрическое уравнение:
1. ;
2. ;
3. 
Тема 9. Решение тригонометрических уравнений
методом группировки и разложения на множители
Пример1: Решить тригонометрическое уравнение
2 sin x cos 2x – 1 + sin x – 2cos 2x = 0
Решение:
Способом группировки разложим левую часть исходного уравнения на множители:
2 cos 2x (sin x – 1) + (sin x –1) = (sin x – 1)(2 cos 2x + 1).
Уравнение (sin x – 1)(2 cos 2x + 1) = 0 равносильно совокупности уравнений (sin x – 1) = 0,
2 cos 2x+ 1 = 0.
a) sin x – 1 = 0, sin x = 1, x =  + 2 Пn, n Î Z;
+ 2 Пn, n Î Z;
б) 2 cos 2x + 1 = 0, cos 2x = -  , 2x = ±
, 2x = ±  + 2Пn, n Î Z, x = ±
+ 2Пn, n Î Z, x = ±  + Пn, n Î Z
+ Пn, n Î Z
Ответ: x =  + 2Пn, n Î Z, x = ±
+ 2Пn, n Î Z, x = ±  + Пn, n Î Z
+ Пn, n Î Z
Пример 2: Решить тригонометрическое уравнение: sin x + cos x = 1.
Решение: Перенесём все члены уравнения влево:
sin x + cos x – 1 = 0,
преобразуем и разложим на множители выражение в левой части уравнения:

Пример 3: Решить тригонометрическое уравнение: cos 2 x + sin x · cos x = 1.
Решение: cos 2 x + sin x · cos x – sin 2 x – cos 2 x = 0,
sin x · cos x – sin 2 x = 0,
sin x · ( cos x – sin x ) = 0,

Пример 4: Решить тригонометрическое уравнение:
cos 2x – cos 8x + cos 6x = 1.
Решение: cos 2x + cos 6x = 1 + cos 8x ,
2 cos 4x cos 2x = 2 cos ² 4x,
cos 4x · ( cos 2x – cos 4x ) = 0,
cos 4x · 2 sin 3x · sin x = 0,
|
|
|
1). cos 4x = 0, 2). sin 3x = 0, 3). sin x = 0,

Задание 1: Решить тригонометрическое уравнение:
1. sin x – sin 2x = 0
2. 
3. 
4. 
Тема 10. Решение тригонометрических уравнений,
решаемые с помощью формул сложения, понижения степени и другим
Пример 1: Решить уравнение: 2 sin x · sin 3x = cos 4x.
Решение: Преобразуем левую часть в сумму:
cos 4x – cos 8x = cos 4x,
cos 8x = 0,
8x =  + π k , kÎ Z
+ π k , kÎ Z
x =  +
+  , kÎ Z
, kÎ Z
Ответ: x =  +
+  , kÎ Z
, kÎ Z
Задание 1: Закончить решение:


по формуле 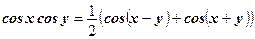

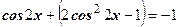

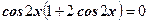
 или
или 
……………………………………………..
Задание 2: Решить тригонометрическое уравнение:
1. 
2. 
3. 
4. 
Тема 11. Решение простейших тригонометрических неравенств
Простейшими тригонометрическими неравенствами называются неравенства вида:

Тригонометрические неравенства могут быть решены по следующему общему правилу.
1. Найти область допустимых значений неизвестной (ОДЗ).
2. Записать соответствующее уравнение, заменив знак неравенства знаком равенства.
3. Решить уравнение, полученное в предыдущем пункте.
4. На числовой оси отметить ОДЗ, корнями уравнения разбить ОДЗ на промежутки.
5. На каждом интервале выбрать одну пробную точку и подставить ее в исходное неравенство. Если неравенство выполняется, то данный интервал необходимо включить в ответ. Если неравенство не выполняется, то интервал следует исключить из рассмотрения.
6. Сделать отбор характерных для неравенства точек – корней уравнения и концов промежутков ОДЗ. Если исходное неравенство нестрогое, то корни уравнения следует записать в ответ, в противном случае – отбросить. Концы промежутков ОДЗ проверить подстановкой в исходное неравенство. Подходящие из них включить в ответ.
Решение неравенств с синусами
|
Неравенства вида sin t < a | |||
| 0< a< 1 | -1< a< 0 | ||
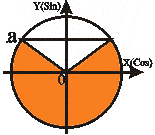 t1 = arcsin a
t2 = - П - arcsin a
t2 < t < t1
-П- arcsin a< t< arcsin a t1 = arcsin a
t2 = - П - arcsin a
t2 < t < t1
-П- arcsin a< t< arcsin a
|  t1 = - arcsin a
t2 = - П + arcsin a
t2 < t < t1
-П+arcsin a< t< -arcsina t1 = - arcsin a
t2 = - П + arcsin a
t2 < t < t1
-П+arcsin a< t< -arcsina
| ||
| Учитывая, что arcSsin(-|a|) = - arcsin |a| и периодичность функции
получаем для любого |a|≤ 1 рещение: -П-arcsin a + 2Пn < t < arcsin a + 2Пn, nÎ Z. | |||
|
Неравенства вида sin t ≥ a | |||
 t1 = arcsin a
t2 = П - arcsin a
t1 ≤ t ≤ t2 t1 = arcsin a
t2 = П - arcsin a
t1 ≤ t ≤ t2
| 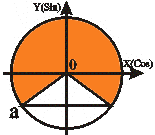 t1 = - arcsin a
t2 = П + arcsin a
t1 ≤ t ≤ t2 t1 = - arcsin a
t2 = П + arcsin a
t1 ≤ t ≤ t2
| ||
| Аналогично объединяем два решения: arcsin a + 2Пn ≤ t ≤ П - arcsin a +2Пn, nÎ Z. | |||
|
|
|






 и
и 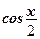 .
.  (? ) Делим на
(? ) Делим на 



 ОДЗ:
ОДЗ: 
 ,
,  , где
, где  ,
,