 |
Решение неравенств с косинусами
|
|
|
|
Решение неравенств с косинусами
|
Неравенства вида cos t ≤ a | |||||||||||||||||
| 0< a< 1 | -1< a< 0 | ||||||||||||||||
 t1 = arccos a
t2 = 2П - arccos a
t1 ≤ t ≤ t2
arccosa≤ t≤ 2П-arccosa t1 = arccos a
t2 = 2П - arccos a
t1 ≤ t ≤ t2
arccosa≤ t≤ 2П-arccosa
|  t1 = П - arccos a
t2 = П + arccos a
t1 ≤ t ≤ t2
П-arccosa≤ t≤ П+arccosa t1 = П - arccos a
t2 = П + arccos a
t1 ≤ t ≤ t2
П-arccosa≤ t≤ П+arccosa
| ||||||||||||||||
| Учитывая, что arccos(-|a|) = П - arccos |a| и периодичность функции получаем для любого |a|≤ 1 рещение: arccos a + 2Пn ≤ t ≤ 2П - arccos a + 2Пn, nÎ Z. | |||||||||||||||||
|
Неравенства вида cos t > a | |||||||||||||||||
 t1 = arccos a
t2 = - arccos a
t2 < t < t1 t1 = arccos a
t2 = - arccos a
t2 < t < t1
|  t1 = П - arccos a
t2 = - П + arccos a
t2 < t < t1 t1 = П - arccos a
t2 = - П + arccos a
t2 < t < t1
| ||||||||||||||||
| Аналогично объединяем два решения: - arccos a + 2Пn < t < П - arccos a +2Пn, nÎ Z | |||||||||||||||||
| |||||||||||||||||
Пример 1: Решить тригонометрическое неравенство:
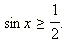
Решение
Нарисуем тригонометрическую окружность и отметим на ней точки, для которых ордината превосходит Для x Î [0; 2π ] решением данного неравенства будут Ответ. |
Задание 1: Решить тригонометрическое неравенство:
1. 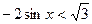
2. 
Проверь себя!
|
|
|
| 1. Найти значение выражения |
| 1). arccos 1+arcsin 0 |
2). arccos(-  )-arcsin )-arcsin 
|
3). tg(arctg  ) )
|
4). sin(arccos  ) )
|
| 2. Решить уравнение: |
| 1). sin3xcosx-sinxcos3x=1 |
| 2). 2cos2x-5cosx=3 |
| 3). tgx-3ctgx=0 |
| 4). sin3x-sinx=0 |
| 5). 2sinx+sin2x=0 |

Подготовка к Единому Государственному экзамену (ЕГЭ)
Прототипы задания В3
Основная идея решения любого тригонометрического уравнения за-
|

|

Тренировочная работа №1
Задание В3: Решите уравнение
|
Уравнение |
Ответ | ||||||||||
| 1. 1. |  В ответе запишите наибольший отрицательный корень уравнения
В ответе запишите наибольший отрицательный корень уравнения
| 1. 1. | | ||||||||
| 1. 2. | 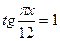 В ответе запишите наименьший положительный корень уравнения
В ответе запишите наименьший положительный корень уравнения
| 1. 2. | | ||||||||
| 1. 3. |  В ответе запишите наибольший отрицательный корень уравнения
В ответе запишите наибольший отрицательный корень уравнения
| 1. 3. | | ||||||||
| 1. 4. |  В ответе запишите наименьший положительный корень уравнения
В ответе запишите наименьший положительный корень уравнения
| 1. 4. | | ||||||||
| 1. 5. |  В ответе запишите наибольший отрицательный корень уравнения
В ответе запишите наибольший отрицательный корень уравнения
| 1. 5. | | ||||||||
| 1. 6. |  В ответе запишите наименьший положительный корень уравнения
В ответе запишите наименьший положительный корень уравнения
| 1. 6. | | ||||||||
| 1. 7. |  В ответе запишите наибольший отрицательный корень уравнения
В ответе запишите наибольший отрицательный корень уравнения
| 1. 7. | | ||||||||
| 1. 8. |  В ответе запишите наименьший положительный корень уравнения
В ответе запишите наименьший положительный корень уравнения
| 1. 8. | | ||||||||
| 1. 9. |  В ответе запишите наибольший отрицательный корень уравнения
В ответе запишите наибольший отрицательный корень уравнения
| 1. 9. | | ||||||||
| 1. 10 | 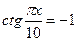 В ответе запишите наименьший положительный корень уравнения
В ответе запишите наименьший положительный корень уравнения
| 1. 10 | | ||||||||
|
Уравнение |
Ответ | ||||||||||
| 1. 11. | 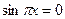 В ответе запишите наибольший отрицательный корень уравнения
В ответе запишите наибольший отрицательный корень уравнения
| 1. 1. | | ||||||||
| 1. 12. |  В ответе запишите наименьший положительный корень уравнения
В ответе запишите наименьший положительный корень уравнения
| 1. 2. | | ||||||||
| 1. 13. | 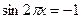 В ответе запишите наибольший отрицательный корень уравнения
В ответе запишите наибольший отрицательный корень уравнения
| 1. 3. | | ||||||||
| 1. 14. |  В ответе запишите наименьший положительный корень уравнения
В ответе запишите наименьший положительный корень уравнения
| 1. 4. | | ||||||||
| 1. 15. |  В ответе запишите наименьший положительный корень уравнения
В ответе запишите наименьший положительный корень уравнения
| 1. 5. | | ||||||||
| 1. 16. |  В ответе запишите наибольший отрицательный корень уравнения
В ответе запишите наибольший отрицательный корень уравнения
| 1. 6. | | ||||||||
| 1. 17. |  В ответе запишите наименьший положительный корень уравнения
В ответе запишите наименьший положительный корень уравнения
| 1. 7. | | ||||||||
| 1. 18. |  В ответе запишите наименьший положительный корень уравнения
В ответе запишите наименьший положительный корень уравнения
| 1. 8. | | ||||||||
| 1. 19. |  В ответе запишите наибольший отрицательный корень уравнения
В ответе запишите наибольший отрицательный корень уравнения
| 1. 9. | | ||||||||
| 1. 20 |  В ответе запишите наибольший отрицательный корень уравнения
В ответе запишите наибольший отрицательный корень уравнения
| 1. 10 | | ||||||||
Задание C1
|
|
|

РЕШЕНИЕ:
1. Решим первое уравнение системы:
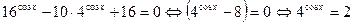
(так как 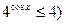
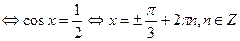
2. Рассмотрим два случая:
а) 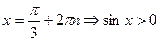
уравнение  решений не имеет;
решений не имеет;
б) 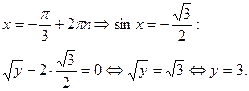
Ответ: 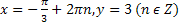
|
|
|



 t1 = arctg a
t2 = - П/2
t2 < t < t1
-
t1 = arctg a
t2 = - П/2
t2 < t < t1
-  < t < arctg a
< t < arctg a
 t1 = - arctg a
t2 = - П/2
t2 < t < t1
-
t1 = - arctg a
t2 = - П/2
t2 < t < t1
-  t1 = arctg a
t2 =
t1 = arctg a
t2 =  t1 = - arctg a
t2 =
t1 = - arctg a
t2 =  1
1
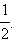
 Ясно также, что если некоторое число x будет отличаться от какого-нибудь числа из указанного интервала на 2π n,
Ясно также, что если некоторое число x будет отличаться от какого-нибудь числа из указанного интервала на 2π n,  то sin x также будет не меньше
то sin x также будет не меньше  Окончательно, получаем, что решениями исходного неравенства будут все
Окончательно, получаем, что решениями исходного неравенства будут все  где
где