 |
Обсуждение методов порядка 4
|
|
|
|
Подойдем теперь вплотную к определению 4-стадийных методов Рунге-Кутты (2.3.1) с таким расчетом, чтобы они имели порядок 4. Для этого необходимо вычислить производные порядков 1, 2, 3 и 4 от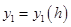 
при 
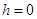и сравнить их с производными точного решения. Теоретически при известных правилах дифференциального исчисления это совершенно тривиальная задача. Однако с использованием (2.3.2) получаются следующие условия:
Эти вычисления очень утомительны и емки. Их громоздкость очень быстро растет для более высоких порядков.
Лемма 1.
Если
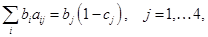(2.4.2)
то уравнения d), g) и h) являются следствием остальных.
Доказательство.
Покажем это для g). C помощью уравнений c) и e) получим:
Для уравнений d) и h) процедура аналогична.
Покажем, что в нашем случае условие
является и необходимым.
Лемма 2.
При 
(2.4.2) следует из уравнений (2.4.1) и уравнений (2.3.2).
Для доказательства потребуется следующая лемма 3.
Лемма 3.
Пусть 
и 
суть 3x3-матрицы, такие что
, (2.4.3)
тогда либо 
, либо 
, где 
.
Доказательство.
Если 
, то из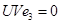 
следует . Если же 
, то существует вектор 
, такой, что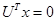 
, и поэтому 
. Но тогда из (2.4.3) следует, что 
должен быть пропорционален вектору 
.
Докажем теперь предыдущую лемму. Введем величины 
для 
. Итак, надо доказать, что 
. Введем теперь матрицы
(2.4.4)
Перемножение этих матриц с использованием условий (2.4.1) дает
, (2.4.5)
причем
Далее последний столбец не может быть нулевым, так как из того, что 
, следует
в силу условия h). Таким образом, из последней леммы следует, что 
. Последнее тождество 
вытекает из равенства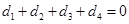 
, которое является следствием условий a) и b).
Теорема.
|
|
|
Если выполнены предположения 
, то уравнения (2.4.1) эквивалентны следующим:
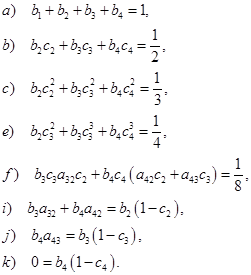(2.4.6)
Доказательство.
Из j) и h) следует, что
. (2.4.7)
Отсюда, в частности, вытекает, что в силу k) 
.
Решение уравнений (2.4.6). Уравнения a)-e) и k) выражают тот факт, что коэффициенты 
и 
являются весами и узлами квадратурной формулы четвертого порядка при 
и . В силу (2.4.7) возможны следующие четыре случая:
1) 
. (2.4.8)
Тогда уравнения a)-e) образуют невырожденную линейную систему для определения 
. Эта система имеет решение:
Остальные три случая с двойными узлами основаны на правиле Симпсона:
2) 
;
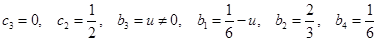3) 
;
4) 
.
После того, как выбраны и 
, получаем 
из уравнения j), и тогда два уравнения f) и i) образуют линейную систему для определения 
и 
.
Определитель этой системы
,
согласно (2.4.7) не равен нулю. Наконец, из того, что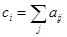 
находим 
, 
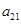и 
.
Особенно популярными стали два варианта, которые выбрал Кутта в 1901 году. Это случай 3) при 
и случай 1) при 
. Оба метода обобщают классические квадратурные формулы, сохраняя их порядок. Первый из них более популярен, однако второй более точен.
Правило 3/8
| 
|
|
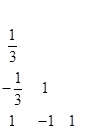
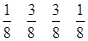
Классический метод Рунге-Кутты
| 
|
|
Оптимальные» формулы
Предпринималось много исследования, чтобы выбрать возможно «лучшие» из множества различных формул Рунге-Кутты 4-го порядка.
Первой попыткой в этом направлении был очень популярный метод, который в 1951 году предложил Гилл. Он преследовал цель уменьшить на сколько возможно количество требуемой машинной памяти («регистров»). Этот метод широко использовался на первых компьютерах в пятидесятых годах и представляет поэтому исторический интерес. Гилл заметил, что больше всего машинной памяти нужно при вычислении 
, когда «требуются регистры для хранения в какой-либо форме» величин
.
Ясно, что для третьей стадии будет достаточно трех регистров, если подлежащие хранению величины линейно зависимы, то есть если
|
|
|
.
Гилл заметил, что это условие удовлетворяется для методов типа 3), если 
. Получающийся метод можно в таком случае переформулировать следующим образом:
В настоящее время производительность компьютеров очень сильно возросла по сравнению с машинами 50-х годов, что привело к прекращению использования данного метода на практике при расчетах. Справедливости ради стоит отметить, что этот метод все-таки рационально употреблять в случаях, когда требуется решать системы дифференциальных уравнений очень высокой размерности со сложными функциями.
|
|
|
