 |
Условия порядков для методов Рунге-Кутты
|
|
|
|
Рассмотрим структуру условий, определяющих порядок метода, или условий порядка, как их называют для краткости. Способ вывода условий порядка прошел большую эволюцию. Он совершенствовался главным образом под влиянием работ Бутчера.
Так как явные методы Рунге-Кутты являются частным случаем неявных, то можем выписать условия, при которых метод имеет заданный порядок.
Метод
|
|
|
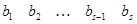
(где на свободных местах должны стоять нули) имеет порядок 
, если удовлетворяется уравнение
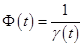(2.6.1)
для каждого дерева 
с корнем и не более чем с разветвлениями[1].
При 
эти условия, обеспечивающие порядок 4, и соответствующие деревья имеют следующий вид:
|  (2.6.2)
|
|  (2.6.3)
|
|  (2.6.4)
|
|  (2.6.5)
|
|  (2.6.6)
|
|  (2.6.7)
|
|  (2.6.8)
|
|  (2.6.9)
|
Заметим, что для меньших значений 
мы берем соответствующее подмножество этих условий, а для меньших 
оставляем лишь некоторые из указанных членов.
Из (2.9) видим, что действительно необходимо 4 этапа, так как если бы их было меньше, то был бы опущен единственный член в левой части этого уравнения. Для явных методов в общем случае выполняется неравенство 
. Фактически (для тех значений, для которых это известно) минимальное значение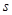 
для данного 
указано в следующей таблице:
|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
|
| 1 | 2 | 3 | 4 | 6 | 7 | 9 |
Общие классы методов с этими значениями и легко найти в случае 
.
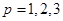Для 
:
| 0 | |
| 1 |
Это известный метод Эйлера.
Для 
:
|
|
|
Это однопараметрическое семейство имеет требуемый порядок для любого ненулевого значения .
Для 
имеется три семейства, из которых первые два таковы:
| 
|
| |
| 
|
|
|
|
|
Каждое из них имеет один параметр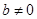 
. Третье семейство имеет в качестве параметров 
и 
, причем
.
Вывод методов с 
более сложен, но его можно упростить, положив
(2.6.10)
(что влечет равенство 
), так как это позволяет опустить уравнения (2.6.3), (2.6.5), (2.6.8) и (2.6.9). Интересно также, что (2.6.10) является следствием (2.6.2) – (2.6.9).
План вывода конкретного метода этого порядка можно выполнить при условии, что не возникает несовместных систем.
Шаг 1. Выбираем значения , и полагаем .
Шаг 2. Из (2.6.2), (2.6.3), (2.6.4) и (2.6.6) находим 
.
Шаг 3. Из уравнения 
(это уравнение есть разность уравнений (2.6.5) и (2.6.7)) находим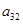 
.
Шаг 4. Из (2.6.10) находим 
.
Шаг 5. Вычисляем 
.
В случае 
шаг 2 приводит к выбору 
и 
при условии, что 
, 
. В частности, имеем известный метод:
| 
|
|
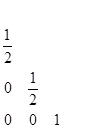
Оценка погрешности и сходимость методов Рунге-Кутты
Со времен работы Лагранжа и особенно Коши всякий установленный численно результат принято сопровождать надежной оценкой погрешности. Лагранж дал известные оценки погрешности многочленов Тейлора, а Коши вывел оценки для погрешности метода ломаных Эйлера. Через несколько лет после первых успехов методов Рунге-Кутты также пришел к заключению, что для этих методов нужны оценки погрешностей[2].
Строгие оценки погрешности
Способ, которым Рунге получил оценку погрешности, делаемой на одном шаге («локальной погрешности»), может быть описан следующим образом. Для метода порядка 
рассмотрим локальную погрешность
(2.7.1)
и воспользуемся ее тейлоровским разложением:
, (2.7.2)
где 
и 
. Явное вычисление 
дает выражение вида
, (2.7.3)
где 
и 
содержат частные производные 
до порядков 
и 
соответственно. Далее поскольку 
, имеем 
. Таким образом, если ограничены все частные производные 
до порядка включительно, имеем 
и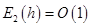 
. Следовательно, существует постоянная 
такая, что 
и
|
|
|
. (2.7.4)
Бибербах использовал несколько иной подход. Запишем
(2.7.5)
и воспользуемся тейлоровскими разложениями
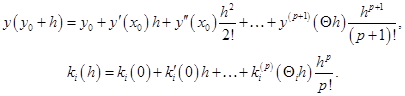(2.7.6)
Для векторных функций эти формулы справедливы покомпонентно (возможно, с различным 
). В силу условий порядка первые члены разложения (2.6.5) по степеням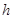 
обращаются в нуль. Таким образом, справедлива следующая теорема.
Теорема.
Если метод Рунге-Кутты (2.3.1) имеет порядок и если все частные производные 
до порядка включительно существуют и непрерывны, то локальная погрешность метода (2.3.1) допускает следующую строгую оценку:
, (2.7.7)
или
. (2.7.8)
Продемонстрируем этот результат, применяя к скалярному дифференциальному уравнению первый метод Рунге-Кутты (2.2.4), который имеет порядок 
. Дифференцируя (2.1.1), получим
. (2.7.9)
Вторая производная величины 
имеет вид
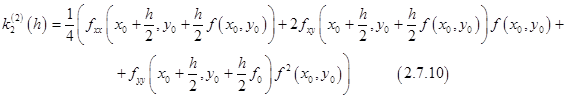
Если условия теоремы выполнены, то легко видеть, что выражения (2.7.9) и (2.7.10) ограничены постоянной, которая не зависит от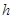 
, что и дает оценку (2.7.8).
Главный член погрешности
Для методов высших порядков строгие оценки погрешностей, подобные (2.7.7), становятся очень непрактичными. Поэтому гораздо более реалистично рассматривать первый ненулевой член в тейлоровским разложении погрешности.
Теорема.
Если метод Рунге-Кутты имеет порядок и если непрерывно дифференцируема 
раз, то для главного члена погрешности имеем:
. (2.7.11)
(2.7.12)
|
|
|
