 |
Оценка глобальной погрешности
|
|
|
|
Глобальной (накопленной) погрешностью[3] называется погрешность численного решения после выполнения нескольких шагов. Пусть мы имеем некоторый одношаговый метод, с помощью которого при заданных начальных данных  и длине шага
и длине шага 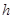 мы определяем численное решение
мы определяем численное решение  , аппроксимирующее
, аппроксимирующее 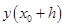 . Воспользуемся обозначениями Хенричи для этого процесса:
. Воспользуемся обозначениями Хенричи для этого процесса:
 , (2.7.13)
, (2.7.13)
и назовем  функцией приращения для данного метода.
функцией приращения для данного метода.
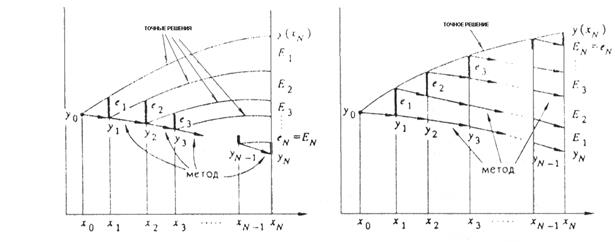
Оценивание глобальной погрешности методами a) и b)
Тогда численное решение в точке 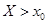 получается с помощью пошаговой процедуры
получается с помощью пошаговой процедуры
, (2.7.14)
и наша задача состоит в оценке глобальной погрешности
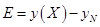 (2.7.15)
(2.7.15)
Эта оценка находится простым способом: локальные погрешности переносятся в конечную точку и затем складываются. Этот «перенос погрешностей» можно выполнить двумя разными способами:
a) перенося погрешность вдоль кривых точных решений; этот способ может дать хорошие результаты, если известны хорошие оценки распространения погрешности для точных решений.
b) перенося погрешность  -го шага посредством выполнения
-го шага посредством выполнения 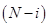 шагов численного метода; этот способ использовали в своих доказательствах Коши (1824) и Рунге (1905), он легко обобщается на многошаговые методы.
шагов численного метода; этот способ использовали в своих доказательствах Коши (1824) и Рунге (1905), он легко обобщается на многошаговые методы.
В обоих случаях оценим сначала локальные погрешности:
 . (2.7.16)
. (2.7.16)
Займемся теперь оценкой перенесенных погрешностей  .
.
a) Теорема.
Обозначим  окрестность точки
окрестность точки  , где
, где 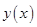 – точное решение уравнения
– точное решение уравнения
 .
.
Пусть в 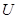 справедливы оценки локальных погрешностей (2.7.16) и выполнено одно из условий:
справедливы оценки локальных погрешностей (2.7.16) и выполнено одно из условий:
 или
или  . (2.7.17)
. (2.7.17)
Тогда имеет место следующая оценка глобальной погрешности (2.7.15):
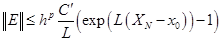 , (2.7.18)
, (2.7.18)
где  ,
,
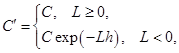
и 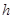 достаточно мало для того, чтобы численное решение оставалось в
достаточно мало для того, чтобы численное решение оставалось в 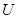 .
.
|
|
|
Доказательство.
При 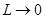 оценка (2.7.18) переходит в
оценка (2.7.18) переходит в  .
.
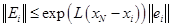 . (2.7.19)
. (2.7.19)
Подставляя в неравенство

выражение (2.7.18) с учетом (2.7.16) и принимая во внимание, что  , приходим к такому неравенству:
, приходим к такому неравенству:
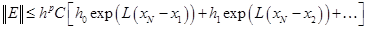 .
.
Выражение в квадратных скобках мажорируется следующими интегралами:
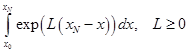 , (2.7.20)
, (2.7.20)
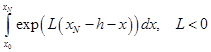 . (2.7.21)
. (2.7.21)
Отсюда вытекает справедливость оценки (2.7.18).
b) При втором способе переноса погрешностей рассмотрим кроме (2.7.14) еще одно численное решение, значения которого в соседних узлах связаны равенством
 .
.
Оценим норму разности 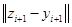 через
через 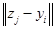 . Для
. Для  формулы метода Рунге-Кутты запишем в следующих обозначениях:
формулы метода Рунге-Кутты запишем в следующих обозначениях:

Вычитая из этих формул соответствующие формулы (2.3.1), получим для норм разностей такие оценки:
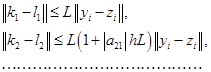

Оценивание римановых сумм методом a) и b)
Пусть  – постоянная Липшица для функции
– постоянная Липшица для функции  и пусть
и пусть 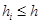 . Тогда функция приращения
. Тогда функция приращения 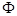 для метода (2.3.1) удовлетворяет неравенству
для метода (2.3.1) удовлетворяет неравенству
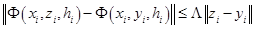 , (2.7.22)
, (2.7.22)
где
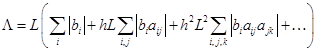 . (2.7.23)
. (2.7.23)
Из (2.7.22) получаем искомую оценку:
 , (2.7.24)
, (2.7.24)
и с её помощью оценку перенесенных погрешностей вместо оценки (2.7.19).
Предположим, что для начальных значений, лежащих на точном решении, локальная погрешность удовлетворяет оценке
 (2.7.25)
(2.7.25)
и что в окрестности решения функция приращения  удовлетворяет неравенству
удовлетворяет неравенству
 . (2.7.26)
. (2.7.26)
Тогда для глобальной погрешности (2.7.15) справедлива следующая оценка:
 , (2.7.27)
, (2.7.27)
где 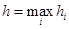 .
.
Оптимальный выбор шага
Предположим, что при интегрировании от точки  до точки
до точки  с шагом
с шагом 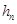 погрешность приближенно равна
погрешность приближенно равна  . Так как это соответствует росту погрешности со скоростью, приблизительно равной
. Так как это соответствует росту погрешности со скоростью, приблизительно равной 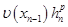 , то
, то 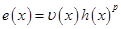 , где
, где  – функция, определяющая шаг. Положим
– функция, определяющая шаг. Положим  и получим оценку интеграла, который приближенно равен полной погрешности:
и получим оценку интеграла, который приближенно равен полной погрешности:

С другой стороны, затраты будут пропорциональны числу шагов, которое приближенно равно
|
|
|

Методами вариационного исчисления можно показать, что если мы хотим минимизировать затраты 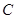 при некотором фиксированном значении погрешности
при некотором фиксированном значении погрешности  , то следует сохранять постоянной величину
, то следует сохранять постоянной величину  . Это означает, что окончательная погрешность должна быть одинаковой на каждом шаге.
. Это означает, что окончательная погрешность должна быть одинаковой на каждом шаге.
В современных программах[4], реализующих методы Рунге-Кутты, обязательно используется некоторый алгоритм автоматического изменения шага интегрирования. Интуитивно ясно, что на участках плавного изменения решения счет можно вести с достаточно крупным шагом. В то же время, на тех участках, где происходят резкие изменения поведения решения, необходимо выбирать мелкий шаг интегрирования. Обычно начальное значение шага задет пользователь или оно определено в программе. Далее шаг интегрирования изменяется в соответствии с величиной, получаемой в ходе вычисления оценки локальной погрешности.
Существует достаточно много способов оценки локальной погрешности, среди которых так называемое правило Рунге. Однако в моей программе я использовал самый простой и в то же время эффективный способ оценки локальной погрешности, который описан в разделе 3.1. «Описание программы Ilya RK-4 версия 1.43». Этот метод базируется на удвоении или делении пополам длины шага в зависимости от отношения локальной погрешности и максимально локальной допустимой погрешности 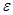 .
.
Практическая часть
|
|
|


