 |
Список использованных источников
|
|
|
|
[1]. Амоносов А.А., Дубинский Ю.А., Копченова Н.В. «Вычислительные методы для инженеров», М., Высшая школа, 1994, 544с.
[2]. Хайрер Э., Нёрсетт С., Ваннер Г. «Решение обыкновенных дифференциальных уравнений. Нежесткие задачи», М., Мир, 1990, 512с.
[3]. Холл Д., Уатт Д. «Современные численные методы решения обыкновенных дифференциальных уравнений», М., Мир, 1979, 312с.
Приложение А. Графики функций
В данном приложении рассмотрены три дифференциальных уравнения первого порядка. К каждому уравнению прилагается по два графика – первый из них построен созданным приложением, а второй создан в пакете Maple 9.01.

Интегральная кривая, построенная приложением «Ilya RK -4 версия 1.43»
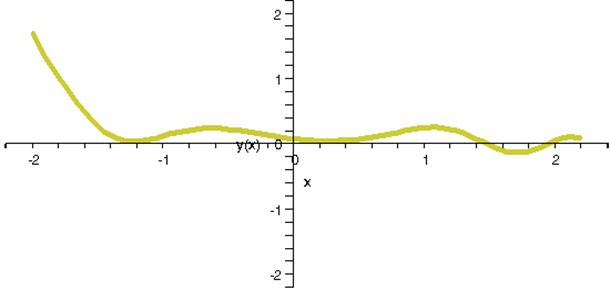
Интегральная кривая, построенная математическим пакетом Waterloo Maple 9.01
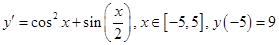

Интегральная кривая, построенная приложением «Ilya RK -4 версия 1.43»

Интегральная кривая, построенная математическим пакетом Waterloo Maple 9.01
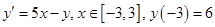

Интегральная кривая, построенная приложением «Ilya RK -4 версия 1.43»
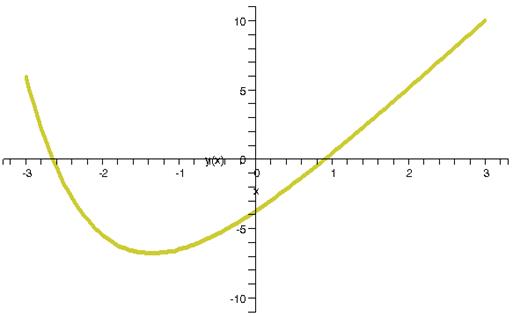
Интегральная кривая, построенная математическим пакетом Waterloo Maple 9.01
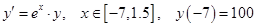

Интегральная кривая, построенная приложением «Ilya RK -4 версия 1.43»

Интегральная кривая, построенная математическим пакетом Waterloo Maple 9.01
Приложение Б.
Пример таблицы значений функции y(x)
y(-7)=100, h=0.4
y(-6.6)=100.045, h=0.4
y(-6.2)=100.112, h=0.4
y(-5.8)=100.212, h=0.4
y(-5.4)=100.361, h=0.4
y(-5)=100.585, h=0.4
y(-4.6)=100.919, h=0.4
y(-4.2)=101.419, h=0.4
y(-3.8)=102.17, h=0.4
y(-3.4)=103.301, h=0.2
y(-3.2)=104.067, h=0.2
y(-3)=105.011, h=0.2
y(-2.8)=106.175, h=0.2
y(-2.6)=107.615, h=0.2
y(-2.4)=109.4, h=0.2
y(-2.2)=111.62, h=0.2
y(-2)=114.392, h=0.2
y(-1.8)=117.873, h=0.2
y(-1.6)=122.267, h=0.2
y(-1.4)=127.857, h=0.2
y(-1.2)=135.033, h=0.2
y(-1)=144.346, h=0.2
y(-0.8)=156.596, h=0.2
y(-0.6)=172.977, h=0.1
y(-0.5)=183.256, h=0.1
y(-0.4)=195.327, h=0.1
y(-0.3)=209.595, h=0.1
|
|
|
y(-0.2)=226.578, h=0.1
y(-0.1)=246.953, h=0.05
y(-0.05)=258.68, h=0.05
y(2.96985e-15)=271.608, h=0.05
y(0.05)=285.897, h=0.05
y(0.1)=301.73, h=0.05
y(0.15)=319.32, h=0.05
y(0.2)=338.919, h=0.05
y(0.25)=360.821, h=0.05
y(0.3)=385.374, h=0.05
y(0.35)=412.989, h=0.05
y(0.4)=444.156, h=0.05
y(0.45)=479.459, h=0.025
y(0.475)=498.877, h=0.025
y(0.5)=519.603, h=0.025
y(0.525)=541.747, h=0.025
y(0.55)=565.433, h=0.025
y(0.575)=590.794, h=0.025
y(0.6)=617.978, h=0.025
y(0.625)=647.149, h=0.025
y(0.65)=678.489, h=0.025
y(0.675)=712.199, h=0.025
y(0.7)=748.501, h=0.025
y(0.725)=787.645, h=0.025
y(0.75)=829.906, h=0.025
y(0.775)=875.592, h=0.025
y(0.8)=925.047, h=0.025
y(0.825)=978.656, h=0.025
y(0.85)=1036.85, h=0.025
y(0.875)=1100.11, h=0.025
y(0.9)=1168.98, h=0.025
y(0.925)=1244.07, h=0.0125
y(0.9375)=1284.16, h=0.0125
y(0.95)=1326.08, h=0.0125
y(0.9625)=1369.91, h=0.0125
y(0.975)=1415.77, h=0.0125
y(0.9875)=1463.78, h=0.0125
y(1)=1514.04, h=0.0125
y(1.0125)=1566.7, h=0.0125
y(1.025)=1621.89, h=0.0125
y(1.0375)=1679.75, h=0.0125
y(1.05)=1740.44, h=0.0125
y(1.0625)=1804.13, h=0.0125
y(1.075)=1871, h=0.0125
y(1.0875)=1941.23, h=0.0125
y(1.1)=2015.04, h=0.0125
y(1.1125)=2092.63, h=0.0125
y(1.125)=2174.24, h=0.0125
y(1.1375)=2260.12, h=0.0125
y(1.15)=2350.54, h=0.0125
y(1.1625)=2445.79, h=0.0125
y(1.175)=2546.16, h=0.0125
y(1.1875)=2652, h=0.0125
y(1.2)=2763.65, h=0.0125
y(1.2125)=2881.49, h=0.0125
y(1.225)=3005.94, h=0.0125
y(1.2375)=3137.43, h=0.0125
y(1.25)=3276.43, h=0.0125
y(1.2625)=3423.46, h=0.0125
y(1.275)=3579.07, h=0.0125
y(1.2875)=3743.83, h=0.0125
y(1.3)=3918.41, h=0.0125
y(1.3125)=4103.47, h=0.0125
y(1.325)=4299.77, h=0.0125
y(1.3375)=4508.11, h=0.0125
y(1.35)=4729.35, h=0.00625
y(1.35625)=4845.11, h=0.00625
y(1.3625)=4964.45, h=0.00625
y(1.36875)=5087.5, h=0.00625
y(1.375)=5214.41, h=0.00625
y(1.38125)=5345.3, h=0.00625
y(1.3875)=5480.34, h=0.00625
y(1.39375)=5619.66, h=0.00625
y(1.4)=5763.44, h=0.00625
y(1.40625)=5911.83, h=0.00625
y(1.4125)=6065, h=0.00625
y(1.41875)=6223.14, h=0.00625
y(1.425)=6386.44, h=0.00625
y(1.43125)=6555.09, h=0.00625
y(1.4375)=6729.28, h=0.00625
y(1.44375)=6909.25, h=0.00625
y(1.45)=7095.2, h=0.00625
y(1.45625)=7287.36, h=0.00625
y(1.4625)=7485.99, h=0.00625
y(1.46875)=7691.33, h=0.00625
y(1.475)=7903.64, h=0.00625
y(1.48125)=8123.19, h=0.00625
y(1.4875)=8350.28, h=0.00625
y(1.49375)=8585.2, h=0.00625
y(1.5)=8828.27, h=0.00625
Приложение В.
Листинг программы «Ilya RK-4 версия 1.43»
// ----------------------------------------------------------------------- //
#include <dos.h>
#include <stdio.h>
#include <conio.h>
#include <math.h>
#include <graphics.h>
#include <stdlib.h>
#define EPSILON 0.00001
#define MAXSTEP 1
#define VERSION 1.43
// ----------------------------------------------------------------------- //
double f(double x, double y);
double do_step(double h, double x_cur, double y_cur);
void title(void);
void main(void);
// ----------------------------------------------------------------------- //
double f(double x, double y)
|
|
|
{
// Правая часть ДУ f(x,y)
return (pow(2.718,x)*y);
}
// ----------------------------------------------------------------------- //
void main(void)
{
int i; // Вспомогательный счетчик
int metka; // Метка на осях
int flag = 0; // Флаг правого конца интегрирования
int metka1, metka2; // Переменные меток на осях координат
double err = 0; // Погрешность
double x0, y0; // Координаты точки начального условия
double big2_step_res, super_step_res; // Результаты длинных шагов
double k = 1; // Коэффициент коррекции
double zoom = 1; // Масштаб на графике
double big_step_res, small_step_res; // Результаты шагов интегрирования
double a, b; // Границы
double temp; // Переменная для служебных нужд
double x_cur, y_cur; // Переменные метода РК
double h; // Шаг интегрирования
double f_max = 0, f_min = 0; // Максимальное и минимальное значение кривой
double norma = 0; // Норма (для корректного масштабирования графика)int c = 8; // Переменная цвета разделительных линий
FILE *myfile; // Указатель на текстовый файл с таблицей значений
// Инициализируем графический адаптер
int gdriver = DETECT, gmode, errorcode;
initgraph(&gdriver, &gmode, "");
errorcode = graphresult();
if (errorcode!= grOk)
{
printf("Ошибка инициализации графики: %s\n", grapherrormsg(errorcode));
getch();
}
textcolor(0);
setbkcolor(0);
title();
printf("y'=f(x,y), y(x0)=y(a)=y0, [a,b] - отрезок интегрирования\n");
label1: printf("\na=");
scanf("%lg", &a);
printf("b=");
scanf("%lg", &b);
// Авто смена границ при необходимости
if (a > b)
{
temp = a;
a = b;
b = temp;
}
if (a == b)
{
printf("Начало отрезка интегрирования совпадает с его концом, повторите ввод!\n");
goto label1;
}
printf("y(%lg)=", a);
scanf("%lg", &y0);
title();
printf("[%lg,%lg] - границы интегрирования, y(%lg)=%lg - начальное условие.\n", a, b, a, y0);
// Инициализация
h = fabs(b - a) / 10;
if (h > 0.1) h = 0.1;
x_cur = a;
y_cur = y0;
f_max = y_cur;
f_min = y_cur;
myfile = fopen("rk4.txt", "w");
fprintf(myfile, "Program: Ilya RK4 Version %g\n", VERSION);
fprintf(myfile, "Method: Runge-Kutta\n");
fprintf(myfile, "The order of method: 4\n");
fprintf(myfile, "Automatic integration step select: Enabled\n");
fprintf(myfile, "[a,b]=[%lg,%lg], y(%lg)=%lg\n", a, b, a, y0);
while (x_cur <= b)
{
if (flag > 1) break;
big_step_res = do_step(h, x_cur, y_cur);
temp = do_step(h / 2, x_cur, y_cur);
small_step_res = do_step(h / 2, x_cur + h / 2, temp);
err = fabs(big_step_res - small_step_res);
// Уменьшение длины шага
if (err > EPSILON)
{
h = h / 2;
continue;
}
// Увеличение длины шага
big2_step_res = do_step(h, x_cur + h, big_step_res);
super_step_res = do_step(2 * h, x_cur, y_cur);
if (fabs(big2_step_res - super_step_res) < EPSILON / 2)
{
h *= 2;
continue;
}
if (h > MAXSTEP) h = MAXSTEP;
|
|
|
// Защита от сбоев
if (h < pow(EPSILON, 2))
{
printf("Ошибка! Возможно, функция разрывна.\nПроинтегрировать на данном интервале невозможно. Скорее всего, g(%lg)=", x_cur);
fprintf(myfile, "Ошибка! Возможно, функция разрывна.\nПроинтегрировать на данном интервале невозможно. Скорее всего, g(%lg)=", x_cur);
if (y_cur < 0)
{
printf("-oo.\n");
fprintf(myfile, "-oo.\n");
}
else
{
printf("+oo.\n");
fprintf(myfile, "+oo.\n");
}
getch();
fclose(myfile);
exit(1);
}
printf("y(%lg)=%lg, err=%lg, h=%lg\n", x_cur, y_cur, err, h);
if (y_cur < f_min) f_min = y_cur;
if (y_cur > f_max) f_max = y_cur;
fprintf(myfile, "y(%lg)=%lg, h=%lg\n", x_cur, y_cur, h);
if (x_cur + h > b) h = fabs(b - x_cur);
x_cur += h;
y_cur = big_step_res;
if (x_cur >= b) flag++;
}
fclose(myfile);
printf("\nТаблица значений записана в файл rk4.txt.\n");
printf("\nНажмите любую клавишу для построения графика...");
flag = 0;
getch();
// Построение графика
cleardevice(); clrscr();
if (fabs(a) > fabs(b)) zoom = fabs(getmaxx() / 2 / a);
else zoom = fabs(getmaxx() / 2 / b);
// Рисуем границы
for (i = 0; i < getmaxy(); i += 5)
{
if (c == 8) c = 0;
else c = 8;
setcolor(c);
line(a * zoom + getmaxx() / 2, i, a * zoom + getmaxx() / 2, i + 5);
line(b * zoom + getmaxx() / 2 - 1, i, b * zoom + getmaxx() / 2 - 1, i + 5);
}
if (fabs(f_min) > fabs(f_max)) norma = fabs(f_min) * zoom;
else norma = fabs(f_max) * zoom;
// Определение коэффициента коррекции
k = (getmaxy() / 2) / norma;
// Предотвращение чрезмерного масштабирования
if (k < 0.0001) k = 0.0001;
if (k > 10000) k = 10000;
for (i = 0; i < getmaxx(); i += 5)
{
if (c == 8) c = 0;
else c = 8;
setcolor(c);
line(i, -y0 * zoom * k + getmaxy() / 2, i + 5, -y0 * zoom * k + getmaxy() / 2);
line(i, -f_min * zoom * k + getmaxy() / 2, i + 5, -f_min * zoom * k + getmaxy() / 2);
line(i, -f_max * zoom * k + getmaxy() / 2, i + 5, -f_max * zoom * k + getmaxy() / 2);
}
metka = ceil((-y0 * zoom * k + getmaxy() / 2) / 16);
if (metka <= 0) metka = 1;
if (metka == 15) metka = 16;
if (metka > 25) metka = 25;
gotoxy(1, metka);
printf("Y=%.2g", y0, metka);
metka = ceil((-f_max * zoom * k + getmaxy() / 2) / 16);
if (metka <= 0) metka = 1;
if (metka == 15) metka = 16;
if (metka > 25) metka = 25;
gotoxy(1, metka);
printf("Y=%.2lg", f_max, metka);
metka = ceil((-f_min * zoom * k + getmaxy() / 2) / 16);
if (metka <= 0) metka = 1;
if (metka == 15) metka = 16;
if (metka > 25) metka = 25;
gotoxy(1, metka);
printf("Y=%.2lg", f_min, metka);
// Пишем границы, делаем отметки на осях координат
metka1 = ceil((a * zoom + getmaxx() / 2) / 8);
if (metka1 < 1) metka1 = 1;
if (metka1 > 75) metka1 = 75;
if (metka == 17) metka = 18;
gotoxy(metka1, 15);
if (a!= 0) printf("%.2lg", a);
metka2 = ceil((b * zoom + getmaxx() / 2 - 1) / 8);
|
|
|
if (metka2 - metka1 < 7) metka2 = metka1 + 7;
if (metka2 < 1) metka2 = 1;
if (metka2 > 75) metka2 = 75;
gotoxy(metka2, 15);
printf("%.2lg", b);
gotoxy(80, 17);
printf("X");
gotoxy(42,1);
printf("Y");
gotoxy(39, 15);
printf("0");
// Рисуем систему координат
setcolor(15);
line(0, getmaxy() / 2, getmaxx(), getmaxy() / 2);
line(getmaxx() / 2, 0, getmaxx() / 2, getmaxy());
line(getmaxx() / 2, 0, getmaxx() / 2 - 5, 10);
line(getmaxx() / 2, 0, getmaxx() / 2 + 5, 10);
line(getmaxx(), getmaxy() / 2, getmaxx() - 10, getmaxy() / 2 + 5);
line(getmaxx(), getmaxy() / 2, getmaxx() - 10, getmaxy() / 2 - 5);
setcolor(10);
h = fabs(b - a) / 10;
if (h > 0.1) h = 0.1;
y_cur = y0;
x_cur = a;
f_max = y_cur;
f_min = y_cur;
x0 = zoom * a + getmaxx() / 2;
y0 = (zoom * (-y_cur)) * k + getmaxy() / 2;
while (x_cur <= b)
{
if (flag > 1) break;
big_step_res = do_step(h, x_cur, y_cur);
temp = do_step(h / 2, x_cur, y_cur);
small_step_res = do_step(h / 2, x_cur + h / 2, temp);
err = fabs(big_step_res - small_step_res);
if (err > EPSILON)
{
h = h / 2;
continue;
}
big2_step_res = do_step(h, x_cur + h, big_step_res);
super_step_res = do_step(2 * h, x_cur, y_cur);
if (fabs(big2_step_res - super_step_res) < EPSILON / 2)
{
h *= 2;
continue;
}
if (h > MAXSTEP) h = MAXSTEP;
line (x0, y0, zoom * x_cur + getmaxx() / 2, zoom * (-y_cur) * k + getmaxy() / 2);
x0 = zoom * (x_cur) + getmaxx() / 2;
y0 = (zoom * (-y_cur)) * k + getmaxy() / 2;
if (x_cur + h > b) h = fabs(b - x_cur);
x_cur += h;
y_cur = big_step_res;
if (x_cur >= b) flag++;
}
while (getch()!= 0);
}
// ----------------------------------------------------------------------- //
void title(void)
{
// Печать заголовка программы
cleardevice(); clrscr();
printf(" Решение дифференциальных уравнений методом Рунге-Кутты 4-го порядка\n");
printf(" с автоматическим выбором длины шага\n");
printf(" Разработал Щербаков Илья, гр. 520212, версия %g\n", VERSION);
printf("____________________________________________________\n");
}
// ----------------------------------------------------------------------- //
double do_step(double h, double x_cur, double y_cur)
{
double k1, k2, k3, k4, delta_y_cur;
k1 = f(x_cur, y_cur);
k2 = f(x_cur + (h / 2), y_cur + (h / 2) * k1);
k3 = f(x_cur + (h / 2), y_cur + (h / 2) * k2);
k4 = f(x_cur + h, y_cur + h * k3);
delta_y_cur = (h / 6) * (k1 + 2 * k2 + 2 * k3 + k4);
return(y_cur + delta_y_cur);
}
// ----------------------------------------------------------------------- //
[1] Дж. Холл, Дж. Уатт «Современные численные методы решения обыкновенных дифференциальных уравнений», М., Мир, 1979, стр. 77.
[2] «Между тем еще нет доказательства, что эти приближенные методы сходятся, или, что практически важнее, нет критерия, определяющего, сколь малым надо сделать шаги, чтобы достичь предписанной точности» – так писал Рунге в 1905 году.
[3] Хайрер Э., Нёрсетт С., Ваннер Г. «Решение обыкновенных дифференциальных уравнений. Нежесткие задачи», М., Мир, 1990, стр. 169.
[4] Амоносов А.А., Дубинский Ю.А., Копченова Н.В. «Вычислительные методы для инженеров», М., Высшая школа, 1994, стр. 445.
[5] Тестирование проводилось на компьютере на базе процессора Intel Pentium 4B. На компьютерах, оснащенных другими процессорами, время выполнения первого и второго этапов может быть другим.
|
|
|


