 |
Процесс пуска ДПТ с независимым возбуждением и переходные процессы при торможении
|
|
|
|
Пуск с помощью 
. 
; 
; 
; 
. При этих условиях
и 
. (4.1)
; 
; 
. (4.2)
Исходные уравнения запишем в виде:
и 
. (4.3)
Рисунок 4.1 – Схема включения и механическая характеристика при пуске двигателя с независимым возбуждением в переходном режиме
Для нахождения 
из первого уравнения определим " I " и подставим его во второе уравнение. Тогда
(4.4)
и окончательно
, (4.5)
Где 
; 
; 
; 
.
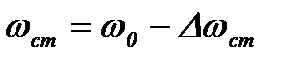Перепишем:
, (4.6)
где
. (4.7)
Из рисунка 4.1 видны слагаемые скорости в переходном режиме.
Решив уравнение находим
(4.8)
При 
и 
. (4.9)
После подстановки " с " и решения относительно " 
" получим
(4.10)
и при x.x.
, (4.11)
т.е. 
изменяется по экспоненте и переходной процесс практически считают законченным через 
с погрешностью 1-2%. Под действием неизменного момента 
ЭД разогнался бы за время 
(прямые Оа и Об).
Для нахождения 
(рисунок 4.2) воспользуемся теми же исходными уравнениями, и будем иметь
(4.12)
и, решив его относительно I, получим
, 
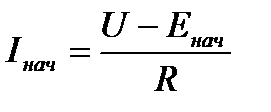. (4.13)
При пуске 
, тогда 
. Тогда уравнение тока:
. (4.14)
И для x.x. пуска
. (4.15)
Учитывая, что , полученные уравнения можно переписать и для " М ". Т.е. ток и момент в переходных режимах также меняются по экспоненте.
Рисунок 4.2 - Зависимости при пуске двигателя с независимым возбуждением
1 – под нагрузкой; 2 – в режиме холостого хода
В случае ступенчатого реостатного пуска расчет каждой ступени производится по приведенным формулам скорости и тока, границами колебаний которого будут 
и 
, заданные нами. Надо иметь при этом ввиду, что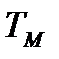 
на каждой ступени другая, соответствующая R -ступени.
Динамическое торможение. Принимаем те же условия, что и при пуске.
Тогда исходные уравнения
и 
; 
(4.16)
Решив систему этих уравнений, получим время переходного процесса
|
|
|
(4.17)
и скорость, до которой будет заторможен ЭД за время " t "
. (4.18)
При торможении, когда на валу есть активная нагрузка 
и будет
; 
. (4.19)
При торможении с x.x.
; 
; 
. (4.20)
При реактивном (трение) торможение закончится в точке А (рисунок 4.3).
Рисунок 4.3 – Скорость двигателя с независимым возбуждением при динамическом торможении: 1 – под нагрузкой; 2 – в режиме холостого хода
Для нахождения решим исходные уравнения относительно I.
(4.21)
в течение
. (4.)
Если ЭД работал вхолостую при 
и 
, то
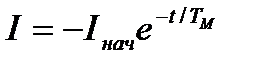. (4.22)
Толчок тормозного тока:
. (4.23)
При x.x.
. (4.24)
При реактивном моменте процесс изменения тока закончится в точке А (рисунок 4.4). Уравнения для тока при 
такие же и для момента. Принимают 
.
Рисунок 4.4 – Зависимости двигателя с независимым возбуждением при динамическом торможении 1 – под нагрузкой; 2 – в режиме холостого хода
Торможение противовключением и реверсирование.
Режим противовключения определяется
, 
, . (4.25)
Меняем полярность обмотки якоря. К валу ЭД приложен активный 
. Определяем " t "
(4.26)
и характер изменения скорости при торможении противовключением и реверсировании ЭД
(4.27)
под нагрузкой 
.
При реверсировании вхолостую
и 
; 
. (4.28)
При реактивном в точке А (рисунок 4.5) 
момент меняет свой знак и кривая скорости имеет излом.
Рисунок 4.5 – Скорость двигателя с независимым возбуждением в режиме противовключения и реверсирования 1 – под нагрузкой; 2 – в режиме холостого хода; 3 – при реактивном моменте
Для определения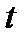 
и 
из исходных уравнений находим
, (4.29)
а для " 
" и " 
" будут те же формулы, что и для режима динамического торможения.
Для реверсирования вхолостую 
толчок тормозного тока
(4.30)
и закон изменения тока будет
. (4.31)
Момент меняется пропорционально току 
. При реверсировании, как и при пуске, скорость, ток и момент будут асимптотически приближаться к установившимся значениям и принимаем 
.
|
|
|
Вопросы для самоконтроля:
1. Дайте определение переходному процессу.
2. Когда переходной процесс считается законченном?
3. Выведете зависимость тока от времени при пуске ДПТ.
4. В чем отличие переходного процесса динамического торможения при активном и реактивном моменте?
Литература [1-5]
|
|
|
