Глава 8. Четырехполюсники. 8. 1 основные определения и классификация четырехполюсников

Глава 8

ЧЕТЫРЕХПОЛЮСНИКИ

8. 1 ОСНОВНЫЕ ОПРЕДЕЛЕНИЯ И КЛАССИФИКАЦИЯ ЧЕТЫРЕХПОЛЮСНИКОВ

 

Часть электрической цепи, рассматриваемая по отношению к любым двум парам ее выводов, называется четырехполюсником (рисунок 8. 1). Понятием «четырехполюсник» пользуются тогда, когда интересуются токами и напряжениями только в двух ветвях или двух парах узлов электрической цепи. Так, в качестве четырехполюсника могут быть представлены длинная линия, электрический фильтр, трансформатор, усилитель, корректирующее и всякое другое устройство с двумя парами выводов, включенное между источником и приемником электрической энергии, когда предметом исследования являются токи и напряжения на этих выводах, а не токи и напряжения внутри самого четырехполюсника.

Выводы четырехполюсника, к которым присоединяется источник электрической энергии, называются входными, а выводы, к которым присоединяется нагрузка, - выходными.

Ради краткости применяются также термины «вход» и «выход» четырехполюсника.

Рисунок 8. 1, Четырехполюсник,

Рисунок 8. 2, Разновидности четырехполюсников.

 

На практике возможны случаи, когда обе пары выводов четырехполюсника являются входными (случай двустороннего питания четырехполюсника) или выходными (случай четырехполюсника, содержащего независимые источники электрической энергии и нагруженного с обеих сторон).

Четырехполюсники могут быть классифицированы по различным признакам.

По признаку линейности элементов, входящих в них, четырехполюсники разделяются на линейные и нелинейные. Ниже рассматриваются линейные четырехполюсники.

По схеме внутренних соединений четырехполюсников различают Г-образный (рисунок 8. 2, а) , Т-образный (рисунок 8. 2, б), П-образный (рисунок 8. 2, в), мостовой (рисунок 8. 2, г), Т-образно - мостовой (рисунок 8. 2, д) и другие.

Четырехполюсники делятся на активные и пассивные.

Четырехполюсник называется активным, если он содержит внутри источники электрической энергии. При этом, если эти источники являются независимыми, то в случае линейного четырехполюсника обязательным дополнительным условием активности четырехполюсника яв­ляется наличие на одной или обеих парах его разомкнутых выводов напряжения, обусловленного источниками электрической энергии, находящимися внутри него, т. е. необходимо, чтобы действия этих источников не компенсировались взаимно внутри четырехполюсника. Такой активный четырехполюсник называется автономным.

В случае, когда источники внутри четырехполюсника являются зависимыми, как это, например, имеет место в схемах замещения электронных ламп и транзисторов, то после отсоединения четырехполюсника от остальной части цепи напряжение на разомкнутых выводах его не обнаруживается. Такой активный четырехполюсник называется неавтономным.

Четырехполюсник называется пассивным, если он не содержит источников электрической энергии; линейный четырехполюсник может содержать источники электрической энергии, взаимно компенсирующиеся таким образом, что напряжения на обеих парах разомкнутых выводов четырехполюсника равны нулю. Так, четырехполюсник на рисунок 8. 3, а пассивен, так как любые две э. д. с. четырехполюсника взаимно компенсируются в контуре (в уравнениях Кирхгофа эти э. д. с. взаимно уничтожаются); четырехполюсник, изображенный на рисунок 8. 3, б, пассивен вследствие того что напряжение на выводах ветви с источниками всегда равно нулю.

Если все э. д. с. в схемах рисунок 8. 3 приравнять нулю, то получатся четырехполюсники, эквивалентные в электрическом смысле исходным. Под эквивалентностью двух четырехполюсников понимается возможность взаимной замены их в электрической цепи без изменения токов и напряжений в остальной ее части.

Рисунок 8. 3. Четырехполюсники, внутри которых действия источников электрической энергии компенсированы.

Различают четырехполюсники симметричные и несимметричные. Четырехполюсник является симметричным в том случае, когда перемена местами его входных и выходных выводов не изменяет токов и напряжений в цепи, с которой он соединен. В противном случае четы­рехполюсник является несимметричным.

Четырехполюсник называется обратимым, если выполняется теорема обратимости, т. е. отношение напряжения на входе к току на выходе, или, что то же, передаточное сопротивление входного и выходного контуров не зависит от того, какая из двух пар выводов является входной и какая выходной. В противном случае четырехполюсник называется необратимым.

Пассивные линейные четырехполюсники являются обратимыми, несимметричные же активные (автономные и неавтономные) четырехполюсники необратимы. Симметричные четырехполюсники всегда обратимы.

Основной смысл теории четырехполюсника заключается в том, что, пользуясь некоторыми обобщенными параметрами четырехполюсника, можно находить токи и напряжения на входе и выходе четырехполюсника.

Сложная электрическая цепь (например, канал связи), имеющая входные и выходные выводы, может рассматривать как совокупность составных четырехполюсников, соединенных по определенной схеме.

Теория четырехполюсника позволяет вычислить параметры такого сложного четырехполюсника по параметрам составных четырехполюсников и, таким образом, получить аналитическую зависимость между токами и на­пряжениями на входе и выходе результирующего слож­ного четырехполюсника, не производя расчетов токов и напряжений внутри заданной схемы.

Получаемые таким путем значения величин на входе и выходе позволяют оценить режим работы передачи в целом. При этом пользование обобщенными параметрами четырехполюсника дает возможность сопоставлять и правильно оценивать передающие свойства электрических цепей, различных по своему типу и структуре.

Теория четырехполюсника позволяет также решать задачи синтеза, т. е. находить структуру и элементы четырехполюсника по заданным характеристикам.

Основы теории пассивного четырехполюсника разрабатывались многими отечественными и зарубежными учеными. Понятие четырехполюсник может быть применено и к механизму, служащему для передачи силы и скорости от источника механической энергии к приемнику. Такой «механический четырехполюсник», имеющий два полюса (вход и выход), может быть описан линейными уравнениями, связывающими силы и скорости на полюсах.

Далее рассмотрим активные (неавтономные) и пассивные четырехполюсники, имеющие одну пару входных и одну пару выходных выводов.

Рисунок 8. 4. Положительные направления токов и напряжений четырехполюсника,

 

Положим, что имеется четырехполюсник, не содержащий независимых источников электрической энергии. Обозначим левую пару выводов четырехполюсника цифрами 1 – 1^/, а правую пару выводов - цифрами 2 - 2'. Этого условного обозначения будем придерживаться во всем последующем изложении, приписывая индексы 1 и 2 токам и напряжениям, относящимся соответственно к левой и правой парам выводов четырехполюсника. Теми же индексами 1 и 2 будут обозначаться входной и выходной контуры четырехполюсника.

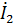На рисунок 8. 4 обозначены принятые положительные направления для токов и напряжений на выводах четырехполюсника. Вариант с токами  и  принято называть прямой передачей (уравнения по форме ||А||), вариант с токами ,  - обратной передачей (уравнения по форме ||В||). Используется также вариант с токами 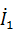, и и который будем называть третьим вариантом (уравнения по формам ||Y||, || Z ||, ||H||, ||G||). Во всех случаях каждое из напряжений   и  понимается как разность потенциалов верхнего (1 или 2) и нижнего (1^/ или 2') выводов четырехполюсника.

Напряжения и токи на выводах четырехполюсника обусловливаются присоединением активных цепей к обеим парам выводов либо присоединением активной цепи к одной паре, а пассивной цепи к другой паре выводов четырехполюсника.

Электрические цепи, присоединенные к выводам 1 – 1^/ и 2 - 2', могут быть на оснований теоремы компенсации в любом режиме замещены источниками э. д. с. Ё₁ = U₁ и Ё₂ = U₂, которые могут рассматриваться как контурные э. д. с., включенные в два независимых контура четырех­полюсника, а токи  =  и 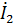 =   - как контурные токи.

Соотношения между напряжениями и токами на входе и выходе четырехполюсника могут быть записаны в виде следующих ниже шести форм уравнений:

1. Форма ||Y||:  =  выражается в зависимости от  и :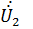

2. Форма ||Z||:  и  выражается в зависимости от :

3. Форма ||A||:  и  выражается в зависимости от :

4. Форма ||B||:  и  выражается в зависимости от :

5. Форма ||H||:  и  выражается в зависимости от :

6. Форма ||G||:  и  выражается в зависимости от :

Из перечисленных выше шести форм уравнений рассмотрим более подробно формы ||Y|| и ||А||.

Коэффициенты и определители каждой системы уравнений четырехполюсника могут быть выражены через коэффициенты и определители любой другой системы. Таблицы облегчают переход от одной формы записи уравнений четырехполюсника к другой.

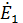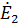Контурные токи  и  связаны с контурными э. д. с. =  и =  (рисунок 8. 4)линейными уравнениями (8. 1), поскольку рассматриваемый четырехполюсник не содержит независимых источников электрической энер­гии.

Коэффициенты Yпредставляют собой входные и выходные проводимости контуров 1 и 2. В общем случае - это комплексные величины, зависящие от частоты; они определяются следующим образом:

 - входная проводимость со стороны выводов 1 при закороченных выводах 2;

 - входная проводимость со стороны выводов 2 при закороченных выводах 1;

 – передаточная проводимость при закороченных выводах 2;

 - передаточная проводимость при закороченных выводах 1;

В случае обратимого четырехполюсника:

(8. 7)

т е. только три коэффициента в уравнениях (8. 1) являются независимыми.

Если четырехполюсник симметричен, то наряду с (8. 7) выполняется условие:

(8. 8)

В этом случае число независимых коэффициентов равно двум (например, Y₁₁ и Y₁₂).

 

8. 3. УРАВНЕНИЯ ЧЕТЫРЕХПОЛЮСНИКА В ФОРМЕ ||А||

 

Как уже отмечалось, при записи уравнений в форме ||А|| положительное направление токов  и 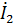 выбирается согласно рисунку 8. 4. Удобство выбора именно такого положительного направления тока  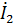связано в данном случае с тем, что форма || А || применяется обычно при передаче электрической энергии от входных выводов к выходным, причем четырехполюсник, включенный между источником и приемником, может состоять из нескольких четырехполюсников, соединенных каскадно; вход каждого последующего четырехполюсника совпадает с выходом предыдущего четырехполюсника.

Выведем форму ||А|| из формы ||Y||. Для этого в уравнениях (8. 1), заменив через 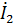, получим:

Из второго уравнения (8. 11) следует:

(8. 12)

Подстановка этого выражения в первое уравнение (8. 11) дает:

(8. 13)

где

Положив в (8. 12) и (8. 13):

                             (8. 14)

получим систему уравнений четырехполюсника (8. 3). Коэффициенты A₁₁, A₁₂, A₂₁, A₂₂ в общем случае комплексные и зависят от частоты: A₁₁ и A₂₂ - безразмерные, A₁₂ имеет размерность сопротивлений, A₂₁ имеет размерность проводимости. Эти коэффициенты могут быть определены аналогично предыдущему следующим образом:

 - отношения напряжений при разомкнутых выходных выводах;

 - отношения ттоков при разомкнутых выходных выводах;

 – величина, обратная передаточной проводимости сопротивлению при закороченных выходах выводах;

 – величина, обратная передаточному сопротивлению при разомкнутых выходах схемы.

Определитель, составленный из коэффициентов А, равен:

(8. 15)

В случае обратимого четырехполюсника Y_a = Y_n, и поэтому:

(8. 16)

т. е. только три любых коэффициента в уравнениях (8. 3) являются независимыми; четвертый коэффициент связан с остальными условием (8. 16).

Если четырехполюсник симметричен, то на основании (8. 14) с учетом (8. 8):

(8. 17)

т. е. число независимых коэффициентов равно двум (например,

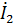В случае перемены направления передачи электрической энергии, а именно при передаче энергии от выводов 2к выводам 1, в уравнениях четырехполюсника связывают напряжения и токи ,   и , \ [уравнения (8. 4) по форме ||В||]. Если заменить в (8. 3) токи Д на -  и  на -   и решить уравнения относительно  и , то получим уравнения четырехполюсника в форме ||В||, выраженные через коэффициенты формы ||А||. Для обратимого четырехполюсника:

Сопоставляя уравнение (8. 18) с уравнениями (8. 3), соответствующими направлению передачи энергии от выводов 1 к выводам 2, заключаем, что с переменой направления передачи энергии коэффициенты А ₁₁ и A₂₂, входящие в системы уравнений, меняются местами.

 

12345678Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: