Это правило распространяется на случай каскадного соединения любого числа четырехполюсника. При этом матрицы, подлежащие

Это правило распространяется на случай каскадного соединения любого числа четырехполюсника. При этом матрицы, подлежащие

Рисунок 8. 11 Последовательное Рисунок 8. 12. Параллельное соедине-

соединение четырехполюсников,     ние четырехполюсников,

перемножению, записываются в порядке следования соответствующих четырехполюсников, так как умножение матриц не подчиняется пере­местительному закону.

Последовательное соединение' четырехполюсников (Рисунок 8. 11) Уравнения составных четырехполюсников в матричной форме II Z || имеют вид:

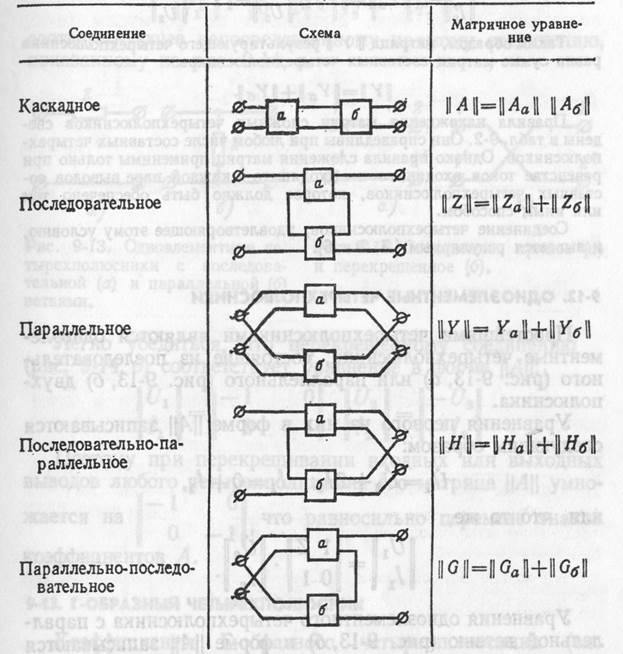
Таблица 9-2

Матричные уравнения сложных четырехполюсников

Таким образом, матрица || Z || результирующего четырехполюсника равна сумме матриц составных четырехполюсников:

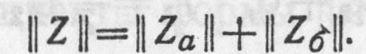
Параллельное соединение четырехполюсника (Рисунок 8. 12)

Уравнения составных четырехполюсников в матричной форме I! У II имеют вид:

При параллельном соединении четырехполюсников:

Таким образом, матрица || У || результирующего четырехполюсника равна сумме матриц составных четырехполюсников

Правила нахождения матриц сложных четырехполюсников све­дены в табл. 9-2. Они справедливы при любом числе составных четырех­полюсников. Однако правила сложения матриц применимы только при равенстве токов входящего и выходящего в каждой паре выводов со­ставных четырехполюсников, которое должно быть обеспечено тем или иным способом.

Соединение четырехполюсников, удовлетворяющее этому условию, называется регулярным [Л. 2 и 6].

 

Простейшими четырехполюсниками являются одноэле­ментные четырехполюсники, состоящие из последователь­ного (Рисунок 8. 13, а ) или параллельного (Рисунок 8. 13, б) двух­полюсника.

Уравнения первого из них в форме ||Л|| записываются следующим образом:

Уравнения одноэлементного четырехполюсника с парал­лельной ветвью (Рисунок 8. 13, б) в форме ||Л|| записываются следующим образом:

Если в первом четырехполюснике (Рисунок 8. 13, а) положить 2 = 0 или, что то же, во втором четырехполюснике (Рисунок 8. 13, б) принять Z —■ оо, то получится уравнение

соответствующее непосредственному прямому соединению, показанному на Рисунок 8. 14, а.

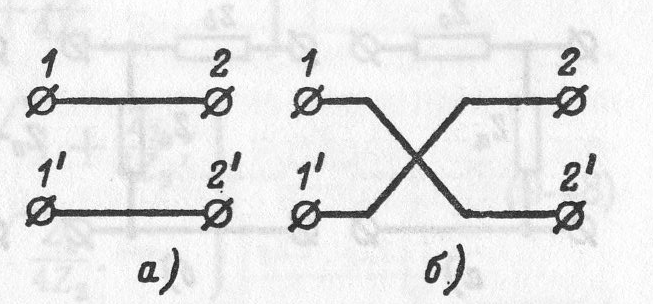
Рисунок 8. 13. Одноэлементные че- Рисунок 8. 14. Соединения: прямое (а) тырехполюсники с последова- и перекрещенное(б), тельной(а)и параллельной (б) ветвями.

Легко убедиться, что перекрещенному соединению (Рисунок 8. 14, б) соответствует уравнение в форме IL4M:

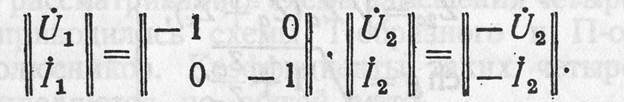
Поэтрму при перекрещивании входных или выходных выводов любого четырехполюсника его матрица ||Л|| умно- — 1                                          011

жается на ^ I что равносильно перемене. знаков

коэффициентов А.

9-13. Г-ОБРАЗНЫЙ ЧЕТЫРЕХПОЛЮСНИК

Коэффициенты Г-образного четырехполюсника (см. Рисунок 8. 15) могут быть получены непосредственно по форму­лам, приведенным в § 9-2 и 9-3. Например, для схемы Рисунок 8. 15,. о коэффициенты формы ||Л|| согласно формулам & 9-3 fwrtVT-

Тот же результат получается на основании (9-26).

Рисунок 8. 17 Разложение симметричных Т-образного(а)и П-образного (б) четырехполюсников на Г-образные.

9-15. СИММЕТРИЧНЫЙ МОСТОВОЙ ЧЕТЫРЕХПОЛЮСНИК

Для симметричного мостового четырехполюсника (см.

Рисунок 8. 18) в соответствии с § 9-3 можно получить коэффициенты фор­мы IL4II:

Рисунок 8. 18. Мостовой четырехполюсник,

Характеристические параметры симметричного мосто­вого четырехполюсника находятся по формулам:

Как уже отмечалось в § 9-5, мостовой четырехполюс­ник является физически реализуемым эквивалентом для любого реально осуществимого симметричного пассивного четырехполюсника [Л. 2 и 16].

⇐ Предыдущая12345678Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: