Главная | Обратная связь | Поможем написать вашу работу!

2.3. Колебания и волны. Механические колебания

2. 3. Колебания и волны

Механические колебания

1. Найти зависимость ускорения гармонического колебания x = x₀ sin (w t + j) от смещения. Построить график зависимости ускорения от смещения.

2. К упругой пружине подвешивают груз, в результате чего пружина растягивается на 2 см. Напишите уравнение гармонических колебаний, складывающихся при условии, что пружина дополнительно растягивается на 2 см и освобождается.

3. Начальная фаза гармонического колебания материальной точки равна нулю. Через какую долю периода скорость точки будет равна половине ее максимальной скорости?

4. Амплитуда гармонического колебания 10 см, период 0, 5 с. Написать уравнение гармонических колебаний. Определить максимальную скорость и максимальное ускорение.

5. Математический маятник с длиной нити 5 м и массой подвешенного тела 0, 1 кг в начальный момент времени находится в положении
равновесия. Маятнику сообщается в горизонтальном направлении начальная скорость 0, 05 м/с. Написать уравнение последующих колебаний маятника.

6. Однородный стержень длиной колеблется около оси, проходящей через его верхний конец. Найти циклическую частоту и период колебаний. Сделать расчёты для м.

7. Обруч, подвешенный на гвозде, совершает малые колебания. Определить период и частоту колебаний обруча, если известно, что радиус обруча R.

8. Однородный картонный диск радиусом R совершает колебания около горизонтально вбитого гвоздя. На каком расстоянии от центра следует пробить отверстие, чтобы период колебаний был минимальным?

9. Льдина толщиной 10 см и площадью 400 см² плавает на поверхности пруда. С какой частотой она будет колебаться, если её несколько погрузить в воду, а затем отпустить?

10. Тело массой m совершает колебания по закону x = x₀ sin w t. Найти его максимальную кинетическую энергию и закон изменения силы, действующей на тело в процессе колебаний.

11. Начальная фаза гармонического колебания материальной точки равна нулю. При смещении точки от положения равновесия на 2, 4 см её скорость см/с, а при смещении, равном 2, 8 см, скорость равна см/с. Найти амплитуду и период колебаний.

12. Найти логарифмический декремент затухания, если у математического маятника длиной 1 м амплитуда колебаний уменьшилась за 1 мин в 2 раза.

13. Амплитуда затухающих колебаний за 1 мин уменьшается в 2 раза. Во сколько раз она уменьшится за 3 мин?

14. Начальная амплитуда колебаний математического маятника A₁ = 20 см, амплитуда после 10 полных колебаний равна A₁₀ = 1 см. Определить логарифмический декремент затухания и коэффициент затухания, если период колебаний T = 5 с. Записать уравнение колебания.

15. К невесомой пружине подвесили грузик, и она растянулась на Dx = 9, 8 см. С каким периодом будет колебаться грузик, если дать ему
небольшой толчок в вертикальном направлении? Логарифмический декремент затухания q = 3, 1.

16. Найти добротность осциллятора, у которого амплитуда смещения уменьшается в h = 2, 0 раза через каждые n = 110 периодов колебаний.

17. Найти добротность осциллятора, у которого собственная частота w₀ = 10 c^–¹ и время релаксации t = 60 с.

18. Во сколько раз изменится период вертикальных колебаний
груза, подвешенного к двум последовательно соединённым одинаковым пружинам, если пружины соединить параллельно?

19. Определить период колебаний ртути, находящейся в U-образной трубке. Площадь сечения трубки S = 0, 3 см², масса ртути m = 121 г.

20. Точка одновременно участвует в двух взаимно перпендикулярных колебаниях, уравнения которых x = A₁ cos w₁ t, y = A₂ sin w₂ t, где A₁ = 8 см, A₂ = 4 см, w₁ = w₂ = 2 c^–¹. Написать уравнение траектории, построить её на чертеже, показать начальное состояние и направление
движения.

21. Определить максимальное ускорение материальной точки, совершающей гармонические колебания с амплитудой A = 15 см, если наибольшая скорость точки см/с. Написать уравнение колебаний.

22. Амплитуда гармонических колебаний материальной точки A = 2 см, полная энергия W = 3× 10^–⁷ Дж. При каком смещении от положения равновесия на колеблющуюся точку действует сила F = 2, 25× 10^–⁵ H?

23. Маленький шарик, подвешенный на нити длиной 20 см, отклоняют на угол 5° и наблюдают его колебания. Найти скорость шарика при прохождении им положения равновесия (двумя способами).

24. При какой скорости поезда маятник длиной 1 м, подвешенный в вагоне, особенно сильно раскачается, если длина рельс между стыками 12, 5 м?

25. В поезде, движущемся равномерно, период колебаний математического маятника. Каким будет период колебаний, если поезд начнёт тормозить с ускорением, равным g / 2?

26. На каком расстоянии от центра нужно подвесить тонкий стержень длиной , чтобы получить физический маятник, колеблющийся
с максимальной частотой? Чему равна эта частота?

27. Найти закон, по которому изменяется натяжение нити математического маятника, совершающего колебания j = j₀ cos w t. Масса маятника m.

28. Написать уравнение гармонического колебания, если максимальное ускорение точки м/с², период колебаний 2 с и смещение точки от положения равновесия в начальный момент времени 2, 5 см.

29. Материальная точка массой m = 0, 01 кг движется по закону 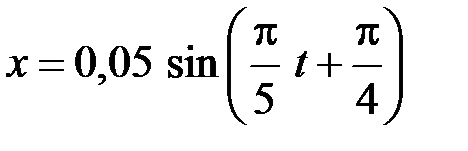м. Найти максимальную силу, действующую на точку и полную энергию колебания.

30. Пружинный маятник массой m = 0, 3 кг совершает колебания с амплитудой A = 5 см. Зная, что полная энергия колебаний равна 1 Дж, найти коэффициент упругости пружины и период колебаний.

31. Медный шарик, подвешенный к пружине, совершает колебания с периодом 1 с. Как и на сколько изменится период колебаний, если медный шарик заменить алюминиевым такого же размера? Плотность меди 8, 9 г/см³, плотность алюминия 2, 7 г/см³.

32. Частота колебаний стального шарика радиусом 1 см, прикрепленного к пружине, в воздухе w₀ = 5 с^–¹, а в жидкости w = 4 с^–¹. Определить вязкость жидкости.

33. Тело движется под действием силы F = F₀ cos w t по закону x = A sin w t. Найти работу за время, прошедшее от момента t₁ до момента t₂. Найти работу силы за один период и среднюю мощность за период.

34. На тело действует сила F = F₀ cos w t. Найти закон движения
тела при начальных условиях при t = 0, x = 0, u = 0. Определить период колебания, наибольшее значение x (t) и наибольшее значение скорости. Масса движущейся частицы m.

35. Определить отношение потенциальной энергии гармонически колеблющейся точки к ее кинетической энергии, если известна фаза колебаний.

36. Материальная точка участвует в двух взаимно перпендикулярных колебаниях x = 2 cos p t / 2 и y = - cos p t. Найдите уравнение траектории.

37. При сложении двух одинаково направленных гармонических
колебаний с одной и той же частотой и амплитудами, равными 2 и 4 см, получается гармоническое колебание с амплитудой 5 см. Найти разность фаз складываемых колебаний.

38. Точка участвует одновременно в двух колебаниях одного направления, которые происходят по законам x₁ = a cos w t и x₂ = a cos 2 w t. Найти максимальную скорость точки.

39. Найти уравнение траектории y (x) точки, если она движется по закону x = a sin w t, y = a sin 2 w t.

40. Найти уравнение траектории y (x) точки, если она движется по закону x = a sin w t, y = a cos 2 w t.

⇐ Предыдущая 5 6 7 8 91011 12 13 14 Следующая ⇒

Воспользуйтесь поиском по сайту: