 |
Построение рядов распределения
|
|
|
|
ПОСТРОЕНИЕ РЯДОВ С ПРОИЗВОЛЬНЫМИ ИНТЕРВАЛАМИ
Статистические ряды распределения – это упорядоченное расположение единиц изучаемой совокупности на группы по группировочному признаку.
Любой статистический ряд распределения состоит из двух элементов:
· из упорядоченных значений признака или вариантов;
· количества единиц совокупности, имеющих данные значения, называемых частотами. Частоты, выраженные в долях единицы или в процентах к итогу, называются частостями.
Для анализа основных социально-экономических показателей используем метод статистических группировок. Метод группировки позволяет «сжать» информацию, полученную в ходе наблюдения и на этой основе выявить закономерности, присущие изучаемому явлению.
С помощью метода группировок решаются следующие задачи:
1. Выявление социально экономических типов явлений.
2. Изучение структуры явления и структурных сдвигов, происходящих в нем.
3. Выявление связей, зависимости между явлениями.
По исходным данным построим интервальный вариационный ряд.
1. проранжируем ряд чисел и сведем их в таблицу:
Таблица 3.1
Группировка населения по среднемесячной заработной плате (руб).
| 1800 | 2070 | 2550 | 3180 | 4400 | 4700 | 4710 | 5230 |
| 5800 | 8050 | 8470 | 8870 | 8890 | 8900 | 12144 | 12260 |
| 12440 | 12700 | 12850 | 13690 | 13700 | 13900 | 14090 | 14680 |
| 15100 | 15730 | 17810 | 18010 | 19100 | 22900 |
Расчеты для таблицы 3.1 Группировка населения по среднемесячной заработной плате (руб.) (1800;2070;2550;3180;4400)
2. Найдем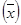 
простое по формуле:
, (3.1)
где xi – i-ый вариант осредняемого признака, n-число вариантов.
=2800
3. Определим среднее квадратичное простое по формуле:
|
|
|
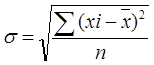, (3.2)
где xi – i-ый вариант осредняемого признака, n-число вариантов, 
- средняя величина признака.
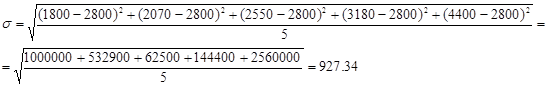
927,34 – обобщающая характеристика размеров вариации признака в совокупности.
4. Определим коэффициент вариации по формуле:
V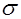 
= 
, (3.3)
где 
- среднее квадратичное простое, 
- средняя величина признака.
Vσ= 
=33.1%
Коэффициент вариации не превышает 33%, следовательно, совокупность считается однородной, первый интервал (1800-4400).
(4700;4710;5230;5800;8050;8470;8870;8890;8900;12144;12260;12440;12700; 12850;13690)
2. Найдем 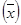простое по формуле (3.1):
3. Определим среднее квадратичное простое по формуле (3.2):
3097,83 – обобщающая характеристика размеров вариации признака в совокупности.
4. Определим коэффициент вариации по формуле (3.3):
Vσ= 
=33.26%
Коэффициент вариации не превышает 33%, следовательно, совокупность считается однородной, и второй интервал (4400-13690).
(13700;13900;14090;14680;15100;15730;17810;18010;19100;22900)
2. Найдем 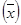простое по формуле (3.1):
= 
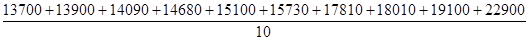=16502
3. Определим среднее квадратичное простое по формуле (3.2):
2792,66 – обобщающая характеристика размеров вариации признака в совокупности.
4. Определим коэффициент вариации по формуле (3.3):
Vσ= 
Vσ=16.92%
Коэффициент вариации не превышает 33%, следовательно, совокупность считается однородной, и третий интервал (13690-22900).
Построим интервальный вариационный ряд, представив его в виде таблицы.
Таблица 3.2
Группировка населения по среднемесячной заработной плате (руб.)
| Группы населения по среднемесячной З.П., руб. | Количество человек | Середины интервалов (xi) | Накопленное количество человек |
| 1800 – 4400 | 5 | 3100 | 5 |
| 4400 – 13690 | 15 | 9045 | 20 |
| 13690 – 22900 | 10 | 18295 | 30 |
| ИТОГО: | 30 | - | - |
В ходе исследования населения Чувашской республике по среднемесячной за-работной плате была выявлена однородная совокупность распределения. По полу-ченной таблице видно, что пять человек получают заработную плату в размере 1800 - 4400 рублей, 15 человек имеют заработную плату 4400 - 13690 рублей и 10 человек с заработной платой 13690 - 22900 рублей. Всего было исследовано 30 че-ловек. В целом население Чувашской республики можно назвать благополучным, так как большее количество населения живет выше прожиточного минимума.
|
|
|
|
|
|
