 |
Общая характеристика исследуемых статистических совокупностей
|
|
|
|
После определения числа групп следует определить интервалы группировки.
Интервал - это значения варьирующего признака, лежащие в определенных границах. Каждый интервал имеет свою величину, верхнюю и нижнюю границы или хотя бы одну из них. Нижней границей интервала называется наименьшее значение признака в интервале, а верхней границей - наибольшее значение признака в нем. Величина интервала (ее еще часто называют интервальной разностью) представляет собой разность между верхней и нижней границами интервала.
Интервалы группировки в зависимости от их величины бывают равные и неравные. Последние делятся на прогрессивно возрастающие, прогрессивно убывающие, произвольные и специализированные.
Если вариация признака проявляется в сравнительно узких границах и распределение носит более или менее равномерный характер, то строят группировку с равными интервалами.
1. Найдем размах по формуле:
, (5.1)
где Xmax-наибольшее значение середины интервалов(хi); Xmin-наименьшее значение середины интервалов (хi).
2. Найдем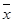 
среднее взвешенное по формуле:
, (5.2)
где xi- значение середины интервалов; fi-число значений.
3. Найдем среднее линейное отклонение взвешенное:
, (5.3)
где xi- значение середины интервалов; fi-число значений.
4. Найдем взвешенную дисперсию по формуле:
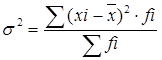, (5.4)
где xi - значение середины интервалов(хi); 
- среднее взвешенное;
fi - число значений.
5. Определим дисперсию относительно условного нуля:
(5.5)
где k - ширина интервала;
А - условный нуль, в качестве которого удобно использовать середину интервала, обладающего наибольшей частотой; 
-так называемый момент второго порядка.
|
|
|
6. Рассчитаем дисперсию по средней арифметической:
или 
(5.6)
7. Найдем среднеквадратичную взвешенную дисперсию по формуле:
, (5.7)
где xi- значение середины интервалов(хi); 
- среднее взвешенное; fi-число значений.
8. Найдем коэффициент осцилляции по формуле:
V 
; 
, (5.8)
где R- размах; 
- среднее взвешенное; Xmax-наибольшее значение середины интервалов(хi); Xmin-наименьшее значение середины интервалов (хi).
9. Найдем коэффициент линейной вариации по формуле:
, (5.9)
где 
- среднее линейное отклонение взвешенное; x- среднее взвешенное.
10. Найдем коэффициент вариации по формуле:
, (5.10)
где 
- это среднеквадратичная взвешенная дисперсия; x- среднее взвешенное.
Расчет для таблицы 3.2 Группировка населения по среднемесячной заработной плате, руб. 1. Найдем размах по формуле (5.1):
R=18295-3100=15195
2. Найдем 
среднее взвешенное по формуле (5.2):
= 
3. Найдем среднее линейное отклонение взвешенное по формуле (5.3):
4. Найдем взвешенную дисперсию по формуле (5.4):
5. Определим дисперсию относительно условного нуля по формуле (5.5):
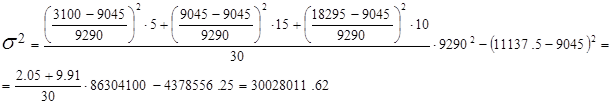
6. Рассчитаем дисперсию по средней арифметической по формуле (5.6):
7. Найдем среднеквадратичную взвешенную дисперсию по формуле (5.7):
8. Найдем коэффициент осцилляции по формуле (5.8):
V 
9. Найдем коэффициент линейной вариации по формуле (5.9):
10. Найдем коэффициент вариации по формуле (5.10):
совокупность не однородная
Расчет для таблицы 3.4 Группировка магазинов по розничному товарообороту, млн. руб. 1. Найдем размах по формуле (5.1):
|
|
|
R=11241-957=10284
2. Найдем 
среднее взвешенное по формуле (5.2):
3. Найдем среднее линейное отклонение взвешенное по формуле (5.3):
4. Найдем взвешенную дисперсию по формуле (5.4):
5. Найдем среднеквадратичную взвешенную дисперсию по формуле (5.7):
6. Найдем коэффициент осцилляции по формуле (5.8):
V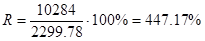 
7. Найдем коэффициент линейной вариации по формуле (5.9):
8. Найдем коэффициент вариации по формуле (5.10):
> 33.3% 
совокупность не однородная
Расчет для таблицы 3.6
Группировка транспортных организаций по грузообороту транспорта общего пользования (млн.т.км)
1. Найдем размах по формуле (5.1):
R=106.74-8.81=97.93
2. Найдем 
среднее взвешенное по формуле (5.2):
3. Найдем среднее линейное отклонение взвешенное по формуле (5.3):
4. Найдем взвешенную дисперсию по формуле (5.4):
5. Найдем среднеквадратичную взвешенную дисперсию по формуле:
1. Найдем коэффициент осцилляции по формуле (5.8):
V 
%
6. Найдем коэффициент линейной вариации по формуле (5.9):
7. Найдем коэффициент вариации по формуле (5.10):
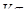=69.05% > 33.3% 
совокупность не однородная
При исследовании группировки населения по заработной плате, совокупность получилась не однородной. При исследовании магазинов по розничному товарообороту совокупность так же оказалась неоднородной. А так же исследованы транспортные организации по грузообороту транспорта общего пользования, где совокупность так же оказалась неоднородной.
|
|
|
