 |
2.2 Колебания частиц среды. Звуковое давление.
|
|
|
|
В процессе распространения колебаний в сплошных средах происходит попеременное сжатие-растяжение слоев среды. Величина смещения частиц среды при звуковых колебаниях зависит не только от времени (как это имеет место для систем с сосредоточенными постоянными (1. 16)), но и от расстояния
(2. 9)
где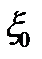 
- амплитуда колебательного смещения; k - волновое число; x - расстояние от источника звука.
Чтобы определить волновое число, заметим, что в точках максимального смещения через один период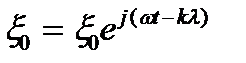 
, что возможно, если 
, т. е.
[1/с] (2. 10)
Колебательная скорость частиц среды
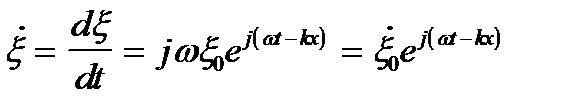(2. 11)
где 
- амплитуда колебательной скорости частиц среды.
Колебательное ускорение
(2. 12)
Следует отметить, что колебательная скорость частиц среды на несколько порядков меньше скорости звука в среде.
Колебания частиц среды вызывают появление в среде переменного давления. Для определения взаимосвязи между звуковым давлением и другими параметрами колебательного процесса рассмотрим уравнение равновесия (система без трения, действуют только силы инерции и упругости) (см. рис. 2. 3). Звуковую волну считаем плоской, т. е. плоскость, проведенная через точки с одинаковой фазой колебаний, будет перпендикулярной направлению распространения звуковой волны
(2. 13)
где S - площадь поперечного сечения волновода; dp - изменение звукового давления на длине dx; r - плотность; 
- колебательное ускорение.
|
|
|
Из (2. 13) определим звуковое давление
с учетом (2. 12) получим:
Постоянная интегрирования с*=0, т. к. при отсутствии колебаний частиц среды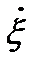 
=0 и р=0, т. е. звуковой волны нет. Отсюда получим
р = r с 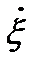[Па] (2. 14)
| S |
| P |
| dx |
| P+dP |
Рис. 2. 3. К определению взаимосвязи между давлением и скоростью колебаний частиц среды
Амплитудное значение звукового давления
р = r с 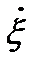0 (2. 15)
Таким образом, звуковое давление прямо пропорционально величине колебательной скорости.
Произведение плотности среды на скорость распространения звуковых колебаний в ней с называют удельным акустическим сопротивлением среды
Z0 = r c [кг/м2с] (2. 16)
Акустическое сопротивление (импеданс) среды в волноводе
ZA= r c/S [кг/м4с] (2. 17)
Между акустическим и механическим импедансами существует взаимосвязь
ZA =ZM /S2
Понятие волновое сопротивление становится яснее из следующего рассуждения. При заданном звуковом давлении, согласно (2. 14) колебательная скорость частиц среды тем больше, чем меньше волновое сопротивление среды. С другой стороны, при постоянной колебательной скорости, создаваемое звуковое давление в среде тем больше, чем больше ее плотность и скорость распространения звука в ней. Например, вследствие вибрации корпуса судна, граничащего с одной стороны с воздушной средой, а с другой - с жидкостью, звуковое давление в воде будет в 3560 раз больше, чем в воздухе, т. к.
раз
Удельное акустическое сопротивление среды при сферической волне
, (2. 18)
где r - радиус сферы, т. е. расстояние от источника звука.
|
|
|
При kr ³ 10 сферическая волна вырождается в плоскую и уравнение (2. 18) дает почти тот же результат, что и (2. 16). Для этого радиус должен быть 
, где l - длина волны.
Интенсивность звука - это энергия, переносимая звуковой волной в единицу времени через единицу поверхности.
Чтобы определить силу звука рассмотрим элементарную работу, совершаемую звуковым давлением на единичной поверхности в плоской волне.
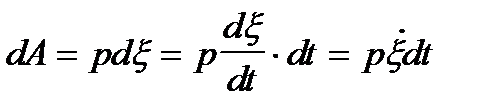
За один период колебаний будет совершена работа
Интенсивность звука за время Т
Подставив сюда выражения мгновенных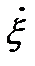 
и р из (2. 11) и (2. 14) получим:
[Вт/м2] (2. 19))
с учетом (2. 15)
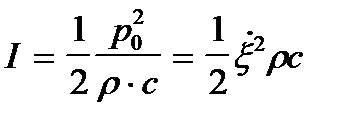(2. 20)
На практике часто используют не амплитудные, а эффективные значения параметров колебательного процесса. Под эффективной величиной переменного параметра понимают величину равноценного ему по энергии, но постоянного во времени параметра (рис. 2. 4). Величина эффективного параметра определяется по формуле
| Рэ |
| Р0 |
| t |
| P |
(2. 21)
|
|
Рис. 2. 4. К понятию эффективного параметра
Интенсивность с учетом (2. 21) 
(2. 22)
По величине интенсивности можно определить мощность источника звука
, [Вт] (2. 23)
С учетом (2. 23) получим:
(2. 24)
При одновременном действии нескольких источников звука с произвольным распределением фаз и частот (некогерентных источников) суммарная их мощность равна сумме мощностей отдельных источников
W = W1 + W2 + W3 +.... + =S Wi (2. 25)
Эффективное значение результирующего звукового давления
(2. 26)
Могут быть частные случаи. Например, если все источники имеют одинаковую частоту и фазу или находятся в противофазе, результирующее звуковое давление определяется алгебраическим суммированием давлений от каждого источника.
|
|
|
