 |
17.7. Уравнения равновесия и движения жидкости. Стационарное движение идеальной жидкости. Уравнение Бернулли
|
|
|
|
Для описания движения жидкостей и газов можно воспользоваться двумя способами. Первый способ Лагранжа, который заключается в том, что изучается движение отдельной частицы. Задается траектория движения частицы, определяются ее скорость и ускорение. Второй способ Эйлера. В этом случае фиксируется точка пространства, и изучаются скорости и ускорения отдельных частиц, проходящих в данный момент через эту точку. Это позволяет говорят о скоростях и ускорениях потока жидкости и газа. Поток жидкости и газа можно охарактеризовать, задав величину и направление скоростей частиц жидкости и газа во всех точках по - тока в каждый данный момент времени.
Поток жидкости или газа изображается графически линиями тока, такими линиями, касательная к которым в каждой точке совпадает по направлению с направлением скорости.
Если частица, пришедшая в какую-либо точку потока, имеет в ней такую же скорость, какую имели в этой точке и все предшествующие частицы, то такой поток жидкости или газа называется стационарным.
В стационарном потоке линии тока совпадают с траекториями движения отдельных частиц.
Часть жидкости или газа, ограниченная линиями тока, называется трубкой тока.
Так как скорость частицы в каждой точке направлена по касательной к линиям тока, то она будет касательной и к поверхности трубки тока. Следовательно, частицы жидкости при своем движении не пересекают стенок трубки тока.
Вся жидкость, прошедшая через одно сечение такой трубки тока, должна пройти и через любое другое ее сечение.
Масса жидкости, прошедшая за время t через какое-либо нормальное сечение трубки тока площадью S
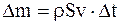, (17. 47)
|
|
|
где v - скорость частиц в этом сечении;
r - плотность жидкости в этом сечении.
В стационарном потоке за одни и те же промежутки времени через два различных сечения S1 и S2 одной и той же трубки тока должны проходить одинаковые массы жидкости. Тогда
(17. 48)
откуда
. (17. 49)
При стационарном потоке изменением плотности жидкости можно пренебречь и считать ее несжимаемой. Следовательно,
. (17. 50)
Так как сечения жидкости были выбраны произвольно, то для несжимаемой жидкости в стационарном потоке величина
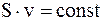. (17. 51)
Полученный результат (17. 51) является математической формой записи теоремы о непрерывности (неразрывности) струи.
Из теоремы о непрерывности струи следует, что при переменном сечении трубки тока, частицы несжимаемой жидкости движутся с ускорением, которое обусловлено непостоянством давления вдоль оси трубки. В местах, где скорость меньше, давление должно быть больше, и наоборот.
Эту теорему можно применять к жидкостям и газам, движущимся со скоростями меньшими скорости звука, т. к. только в этом случае их можно считать, с определенной степенью точности, несжимаемыми.
Рассмотрим количественную связь между скоростью течения и давлением жидкости. При этом будем предполагать, что силы вязкости отсутствуют, т. е. будем рассматривать идеальную (невязкую) жидкость.
Выделим в стационарном потоке участок трубки тока с сечениями S1 и S2. Пусть скорости течения жидкости и давления через эти сечения соответственно равны v1 и v2; p1 и p2. Высоты, на которых находятся центры этих сечений h1 и h2. Тогда, так как силы трения отсутствуют, то можно применить закон сохранения энергии, согласно которому изменение энергии, рассматриваемого элемента жидкости, должно быть равно работе внешних сил, которыми в данном случае являются силы тяжести и силы давления.
|
|
|
За малый промежуток времени Dt, сечение S1 может сместиться на расстояние Dl1=v1∙ Dt, а правое S2 - на Dl2 = v2∙ Dt.
При умножении Dl1 и Dl2 соответственно на S1 и S2 будем иметь объемы жидкости, прошедшие через сечения S1 и S2 за указанное время, которые в силу теоремы о неразрывности струи будут равны между собой
(17. 52)
Следовательно,
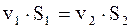. (17. 53)
Первый объем имеет:
а) массу
; (17. 54)
б) потенциальную энергию
; (17. 55)
в) кинетическую энергию
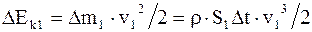. (17. 56)
Аналогично, второй:
а) массу
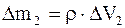; (17. 57)
б) потенциальную энергию
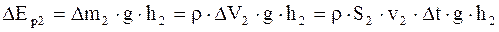; (17. 58)
в) кинетическую энергию
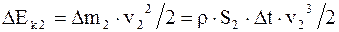. (17. 59)
Изменение полной механической энергии выбранной системы
.
(17. 60)
Силы тяжести и силы давления на боковую поверхность перпендикулярны в каждой точке к направлению перемещения частиц, следовательно, они работы не совершают. Работа совершается лишь силами давления, приложенными к сечениям S1 и S2, которая равна
. (17. 61)
Приравнивая изменение полной энергии к работе внешних сил, будем иметь
. (17. 62)
После сокращения на DV
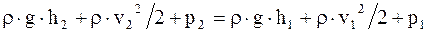. (17. 63)
Так как сечения S1 и S2 были выбраны произвольно, то можно утверждать, что в любом сечении трубки тока справедливо выражение
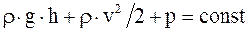. (17. 64)
Выражение (17. 64) становится более точным при S®0, то есть если его применять к двум произвольным точкам одной и той же трубки тока.
Таким образом, в стационарно текущей идеальной жидкости вдоль любой линии тока выполняется условие
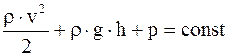. (17. 65)
Выражение (17. 65) является уравнением Бернулли.
Уравнение Бернулли оказывается справедливым для реальных жидкостей, для которых вязкость мала. Оно устанавливает закон изменения давления с изменением высоты h и скорости потока v.
Если v1 = v2 для двух сечений, то на основании (17. 65)
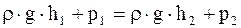или 
, (17. 66)
то есть разность давлений оказывается такой же как и в покоящейся жидкости.
Для горизонтального потока (h1 = h2)
. (17. 67)
Изменение давления в потоке возникает только за счет изменения скорости потока. Давление оказывается меньше там, где скорость больше. Соотношение (17. 67) можно переписать в виде
|
|
|
. (17. 68)
Следовательно, в общем виде
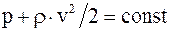, (17. 69)
где p - давление, не зависящее от скорости (статическое давление жидкости);
rv2/2 - давление зависящее от скорости (динамическое давление, которое показывает на какую величину изменяется статическое давление при остановке движущегося потока жидкости).
Из выражения (17. 69) можно сделать вывод, что давление потока жидкости в любом сечении постоянно.
Сумма статического и динамического давлений называют полным давлением потока.
Статическое и полное давления измеряют с помощью манометрических трубок (трубок измеряющих давление - трубок Пито).
Если манометрическая трубка имеет отверстие, расположенное навстречу потоку жидкости, то статическое давление передается в нее согласно закону Паскаля. Кроме того частицы жидкости, попавшие в отверстие, останавливаются, следовательно, их скорость становится равной нулю (v = 0), а это означает - динамическое давление тоже становится равным нулю. В результате статическое давление увеличивается на величину, равную динамическому давлению (r∙ v2/2). Таким образом, такая трубка Пито измеряет полное давление.
Если отверстие в манометрической трубке направлено вниз так, что движущиеся частицы жидкости скользят по поверхности сечения отверстия трубки, то в такую трубку передается только статическое давление, то есть она в этом случае измеряет только статическое давление. При наличии двух рассмотренных трубках, по разности высот столбов жидкости в них можно определить динамическое давление.
Система трубок Пито применяется для создания приборов - манометров. Проградуировав манометр в значениях скорости v, можно получить прибор для измерения скорости потоков жидкости.
Все вышеизложенное относится и к потокам газов.
|
|
|
