 |
17.4. Поверхностные явления на границе раздела двух жидкостей или жидкости и твердого тела
|
|
|
|
Рассматривая поверхностные явления, мы пренебрегали взаимодействием между молекулами жидкости и молекулами пара или газа над ее поверхностью. Оказывается, что если поверхность одной жидкости образует границу раздела с поверхностью другой жидкости или поверхностью твердого тела, то пренебрегать этими силами взаимодействия нельзя. В этом случае коэффициенты поверхностного натяжения одной и той же жидкости значительно изменяется с изменением сред, с которыми соприкасается данная жидкость. Например, если вода при комнатной температуре граничит с бензолом то d= 0, 033 Н/м, с эфиром - d = 0, 012 Н/м, с собственным паром - d = 0, 073 Н/м.
Рассмотрим поверхностные явления, происходящие на границе раздела двух не смачивающихся жидкостей. В каждой точке периметра капли 1, находящейся на поверхности среды 2 будет действовать три силы поверхностного натяжения: F 12, F 13, F 23, направленные по касательным к соответствующим границам раздела сред. Равнодействующая сил поверхностного натяжения F 12 и F 13 направлена внутрь капли и стремится стянуть ее. Сила поверхностного натяжения F 23 стремится растянуть эту каплю. Условие равновесия капли на поверхности жидкости 2 можно записать так
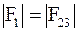, (17. 27)
где 
т. е.
. (17. 28)
Поделив выражение (17. 28) на длину периметра капли l, будем иметь
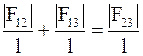или 
. (17. 29)
Если учесть, что максимальное значение s1= s12 + s13, то при s1³ s23 равновесие капли на поверхности другой жидкости возможно, а при s1< s23 капля растекается по поверхности в виде тонкой пленки толщиной в один слой молекул. Такие слои называют мономолекулярными. Зная объем растекшейся жидкости и площадь мономолекулярного слоя, можно вычислить размер одной молекулы (~10-10 м). Надо отметить, что углы q и q внутри капли между касательными к ее поверхности и поверхностью жидкости 2 называют краевыми углами.
|
|
|
Если капля жидкости лежит на поверхности твердого тела (рис. 17. 6), то в каждой точке ее периметра также действуют три силы поверхностного натяжения F 12, F 13, F 23. Результирующая сила
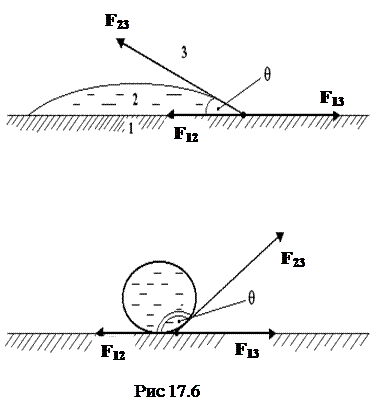F 1 = F 12 + F 13
будет стремиться стянуть каплю, а сила F 23 - растянуть. Условие равновесия капли в этом случае можно записать так
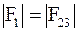, (17. 30)
где
,
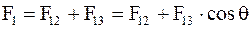т. е.
(17. 31)
или после деления (17. 31) на длину периметра кап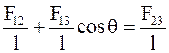ли
или 
. (17. 32)
Из (17. 32) можно сделать следующие выводы:
1. Если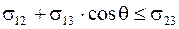 
, то сила F 23 будет растягивать каплю до тех пор, пока угол q не уменьшится до значения, при котором наступит условие равновесия ( ), либо равновесие не наступит. Условие равновесия не наступает в том случае, когда 
. В этом случае капля растечется в тонкую пленку.
2. Если 
, то капля стягивается к центру и угол q увеличивается до тех пор, пока не наступит равновесие, либо при больших s12 значениях (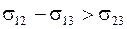 
) капля будет стремиться приобрести сферическую форму.
Таким образом, при остром краевом угле (q< p/2) жидкость растекается по поверхности твердого тела, смачивает его поверхность. Условие смачивания поверхности твердого тела жидкостью
.
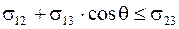Условие абсолютного смачивания
.
При тупом краевом угле (q > p/2) капля стремится стянуться в точку. Жидкость не смачивает поверхность твердого тела. В этом случае условие несмачивания имеет вид
.
Условие абсолютного несмачивания можно записать так
.
Не смачиванием объясняется такие явления как " плавание" тяжелых предметов на поверхности жидкости и " перенос воды в решете".
17. 5. Капиллярные явления. Закон Жюрена
Изменение высоты уровня жидкости в узких трубах (капиллярах) или зазорах между двумя стенками получило название капиллярности.
|
|
|
Явления капиллярности связаны с взаимодействием между молекулами жидкости и твердого тела, с явлением смачивания. При капиллярных явлениях происходит искривление поверхности жидкости, что в свою очередь влечет к появлению дополнительного давления, под действием которого уровень жидкости в капиллярах либо поднимается, если жидкость смачивает его поверхность, либо опускается, если жидкость несмачивает поверхность капилляра. Высота подъема (опускания) жидкости в капиллярах зависит от его радиуса (рис. 17. 7).
Предположим, что жидкость смачивает стенки капилляра, образуется вогнутый мениск, радиус кривизны которого R. Дополнительная сила, обусловленная кривизной поверхности, направлена вверх к центру кривизны. Она создает дополнительное давление, под действием которого жидкость поднимается на высоту h. Подъем жидкости будет продолжаться до тех пор, пока дополнительное давление Dp не уравновесит гидростатическое давление p, т. е.
, (17. 33)
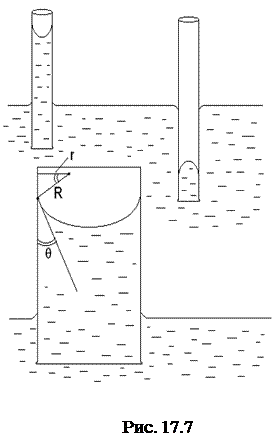где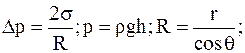 
R - радиус кривизны поверхности жидкости;
r - радиус капилляра.
Таким образом, имеем
; 
,
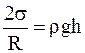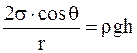откуда
. (17. 34)
Из выражения (17. 34) можно сделать выводы:
1. При q = 0 - жидкость полностью смачивает стенки капилляра. В этом случае
; (17. 35)
2. При q> p/2 жидкость не смачивает стенки капилляра h< 0, т. е. уровень жидкости в капилляре ниже уровня этой жидкости в сосуде.
В узком зазоре между погруженными в жидкость параллельными пластинами также происходит поднятие или опускание жидкости. При этом мениск имеет цилиндрическую форму. Его радиус кривизны связан с расстоянием d между пластинами соотношением
. (17. 36)
В этом случае дополнительное давление 
, а условие равновесия столба жидкости имеет вид
. (17. 37)
Высота подъема жидкости
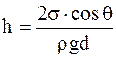. (17. 38)
Уравнение (17. 38) отображает закон Журена. Капиллярные явления приводят к возникновению значительных сил сцепления между смачиваемыми пластинами. Например, в узком зазоре между стеклянными пластинками в 10-6 м, Dp ~ 1, 41× 105 Па, т. е. пластинки размером 0, 1х 0, 1 м притягиваются с силой около 1400 Н. Это связано с тем, что, за счет искривления поверхности жидкости, давление между пластинами меньше атмосферного на величину
|
|
|
,
где R = d/2.
Капиллярные явления играют существенную роль в природе и технике. За счет капиллярных явлений происходит подъем воды из почвы по стволам деревьев и растительности, подъем влаги по стенам домов и сооружений. Осуществляются процессы, связанные с кровообращением, впитывание влаги фильтровальной бумагой, подъем керосина вдоль фитиля в керосиновых лампах и т. д.
17. 6. Кинематическое описание движения жидкости
Разделы механики, в которых изучаются движения жидкостей и газов называются гидро - и аэромеханикой.
Гидро - и аэромеханика, в свою очередь подразделяется на гидро - и аэростатику, в которой изучается равновесие жидкостей и газов, и гидро - и аэродинамику, в которой изучается движение жидкостей и газов совместно с причинами, порождающими это движение.
Общим свойством жидкостей и газов является изменение их объема, формы под действием сколь угодно малых сил.
При изменении объема и формы жидкости в них возникают конечные силы, которые уравновешивают действие внешних сил. Следовательно, жидкости и газы ведут себя также как и твердые тела. Поэтому жидкость и газ, также как и упругие твердые тела, разбиваются на отдельные малые объемы, в которых отдельные атомы и молекулы движутся одинаково. К этим малым элементам жидкостей и газов применимы общие законы механики системы точек, не связанных жестко между собой. Если рассматривается покоящиеся жидкость или газ, или их движения, при которых взаимное расположение отдельных элементов не изменяется, то, с определенной степенью точности, к объемам таких жидкостей можно применять законы динамики твердого тела. В этом случае можно говорить о: центре тяжести объема, моменте сил, действующем на объем, условие равновесия жидкости или газа и т. д., то есть объем жидкости или газа считается отвердевшим. Такой метод изучения жидкостей и газов получил название принципа отвердевания.
Отдельные части жидкостей и газов действуют друг на друга или на соприкасающиеся с ними тела с силой, зависящей от степени их сжатия. Это воздействие характеризуется величиной называемой давлением. Так как сила, действующая со стороны одного элемента на другой, всегда нормальна к площадке, на которую она действует, то давление
|
|
|
. (17. 39)
Давление скалярная величина и не зависит от ориентации площадки dS. Это можно доказать воспользовавшись принципом отвердевания и условием равновесия твердого тела.
Выделим в каком - либо месте некоторый объем жидкости в виде трехгранной призмы. В этом случае на каждую из граней будут действовать силы:
, 
, 
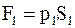. (17. 40)
Сечение призмы будем считать столь малым, чтобы давлением жидкости на торцевые грани So можно пренебречь.
Так как система должна находится в равновесии, то должно выполняться условие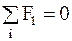 
, то есть
. (17. 41)
При этом силы образуют треугольник подобный треугольнику сечения призмы. Тогда, разделив величину силы, действующей на грань, на длину соответствующей грани, будем иметь:
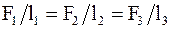. (17. 42)
Так как l1®S1, l2®S2, l3®S3, то
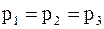. (17. 43)
Поскольку ориентация призмы в пространстве была выбрана произвольно, то, следовательно, величина давления действительно не зависит от ориентации площадки.
При исследовании давления в различных точках покоящихся жидкостей и газов можно применять условие равновесия твердого тела, однако, в этом случае нельзя пренебрегать силами тяжести, как это делалось при рассмотрении малого объема.
Рассмотрим распределение давления в жидкости, находящейся в поле сил тяготения. Для этого выделим в жидкости горизонтально расположенный цилиндрический объем сечением S.
Так как сила тяжести направлена вертикально, то ее составляющие в горизонтальном направлении равны 0. Следовательно, вдоль оси цилиндра будут действовать только две силы 
тогда по условию равновесия 
, т. е.
. (17. 44)
Таким образом, во всех точках жидкости, лежащих на одном уровне, давление имеет одинаковую величину.
Если взять такой же, но вертикально расположенный цилиндр, то в этом случае вдоль его оси, кроме сил давления будет действовать и сила тяжести равная
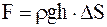, (17. 45)
где r - плотность жидкости;
h - высота цилиндра.
В этом случае условие равновесия будет иметь вид
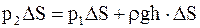или 
. (17. 46)
Следовательно, давление на двух разных уровнях отличаются на величину, равную весу вертикального столба жидкости, заключенного между этими уровнями, с площадью сечения, равного единице.
Следствием разного давления на разных уровнях в жидкостях и газах является наличие выталкивающей силы (силы Архимеда), действующей на тела, которые находятся в них.
|
|
|
Чтобы тело, погруженное полностью в жидкость или газ, находилось в равновесии, выталкивающая (подъемная) сила и сила тяжести должны быть равны. Эти силы должны находиться на одной прямой. Т. е. центр тяжести тела и центр тяжести вытесняемого жидкости объема должны лежать на одной вертикальной прямой, причем центр тяжести тела должен лежать ниже центра тяжести этого объема. Это условие выполняется при проектировании и строительстве подводных и летательных устройств.
|
|
|
