 |
Лекция 16. Кинетические явления (явления переноса)
|
|
|
|
Лекция 16. Кинетические явления (явления переноса)
Понятие о физической кинетике. Диффузия, теплопроводность в газах, жидкостях и твердых телах. Коэффициенты диффузии и теплопроводности. Вязкость жидкостей и газов. Коэффициент вязкости жидкостей и газов. Динамическая и кинематическая вязкости.
16. 1. Понятие о физической кинетике. Вязкость жидкостей и газов. Коэффициент вязкости жидкостей и газов. Динамическая и кинематическая вязкости
При хаотическом движении молекулы газа переходят из одних точек пространства в другие, перенося при этом массу, энергию и количество движения (импульс). Это приводит к возникновению процессов, называемых кинетическими явлениями (явлениями переноса). Кинетические явления (явления переноса) это необратимые процессы, сопровождающиеся переносом какой-либо физической величины, в результате стремления любой системы перейти из неравновесного состояния в равновесное состояние.
Кинетические явления в молекулярной физике: вязкость, теплопроводность, диффузия.
Вязкость (внутреннее трение) - явление переноса, в результате которого происходит перенос количества движения (импульса) молекул из одного слоя газа или жидкости в другой.
Из гидродинамики известно, что сила вязкости, действующая на пластинку S, может быть определена по формуле
(16. 1)
где du/dz - градиент скорости в направлении z;
h – коэффициент сдвиговой (динамической) вязкости. Коэффициент динамической вязкости - физическая величина, численно равная силе внутреннего трения между двумя слоями жидкости или газа единичной площади при градиенте скорости равном единице;
S – величина поверхности, к которой приложена сила F (рис. 16. 1).
|
|
|
Данное уравнение является математической формой записи закона Ньютона в гидро- и газодинамике.
Кроме коэффициента динамической вязкости вводится в рассмотрение коэффициент кинематической вязкости. Коэффициент кинематической вязкости - отношение динамической вязкости к плотности вещества
ν = η /ρ. (16. 2)
Уравнение (16. 1) можно получить из молекулярно кинетических представлений. Предположим, что имеется некоторый слой газа, находящийся между двумя параллельными пластинами. Выделим в слое газа площадку S с площадью в 1 м2, параллельную пластинам " аа" и " вв". В одну секунду через нее будет проходить сверху вниз n молекул. Так как плотность газа не меняется, то, следовательно, такое же количество молекул будет проходить через эту же пластину и снизу вверх. Молекулы, движущиеся сверху вниз, будут иметь скорость (u1 + du1), а движущиеся снизу вверх - (u1 + du1). В результате перехода молекулы газа будут переносить из одного слоя в другой некоторый импульс (количество движения). Количество движения, перенесенное в 1 с через площадку S молекулами, движущимися сверху вниз
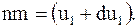(16. 3)
Снизу вверх
(16. 4)
Изменение количества движения молекул за 1с равно
(16. 5)
Это изменение количества движения равно действующей силе, в данном случае силе вязкости
(16. 6)
Таким образом, сила вязкости возникает как следствие перехода молекул при их хаотическом движении из слоев газа, движущихся с меньшими скоростями, в слои газа, движущиеся с большими скоростями. Каждая молекула участвует в двух движениях: хаотическом - тепловом, при этом ее средняя скорость v, и упорядоченном движении со скоростью u, которая меньше v (|u|< < |v|). Попав в соседний слой, молекула претерпевает соударения с молекулами этого слоя. В результате чего она либо отдает избыток своего импульса другим молекулам (если она перешла из слоя, движущегося с большей скоростью), либо увеличивает свой импульс за счет других молекул (если она перешла из слоя, движущегося с меньшей скоростью). В итоге импульс более быстро движущегося слоя убывает, а более медленного слоя возрастает.
|
|
|
Сила, с которой взаимодействуют два смежных слоя, равна импульсу, передаваемому молекулами через поверхность раздела за секунду
|
|
|
