16.2. Диффузия и теплопроводность. Коэффициенты диффузии и теплопроводности

.                              (16. 7)

Уравнение (16. 7) отличается от уравнения (16. 1) отсутствием коэффициента вязкости. Рассчитаем коэффициент вязкости. Для этого предположим:

1) все направления движения молекул равноправны, т. е. в системе координат XOYZ одна треть молекул движется в направлении оси OX, одна треть молекул в направлении оси OY и одна треть молекул в направлении оси OZ;

2) все молекулы движутся с одинаковой средней скоростью < u> и имеют одну и ту же среднюю длину свободного пробега < l>.

Для подсчета числа молекул, прошедших через площадку в каком-либо направлении за 1 с, построим прямой параллелепипед с основанием S равным 1 м² и высотой, численно равной < u> (рис. 16. 2). Если в 1 м³ газа содержится n_o молекул, то в этом параллелепипеде их находится n_o× < u>. Вдоль оси координат, совпадающей с высотой параллелепипеда, будет двигаться только 1/3× n_o× < u> молекул. При этом можно считать, что половина из них движется сверху вниз, а половина - снизу вверх, т. е. искомое число молекул

.                                    (16. 8)

Так как все молекулы имеют одну и ту же длину свободного пробега < l>, то очевидно, что именно с этого расстояния и будут доходить молекулы до площадки S без соударений, тогда

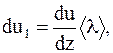                                  (16. 9)

где du/dz - градиент скорости в направлении z.

Следовательно, сила вязкости

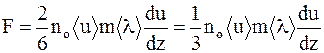.                 (16. 10)

Сравнивая данное выражение с формулой для силы вязкости, полученной Ньютоном (16. 1)  при S = 1 м², для коэффициента вязкости, будем иметь

 или 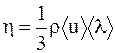.           (16. 11)

где n₀ - число молекул в единице объема;

< u> - средняя скорость теплового движения молекул;

m - масса молекулы;

< l> - средняя длина свободного пробега молекул.

r = n₀× m - плотность жидкости или газа.

Из полученного выражения можно сделать вывод: так как u не зависит от давления, а l ~ 1/p, r ~ p, то коэффициент вязкости не зависит от давления. Это связано с тем, что уменьшение давления газа уменьшает число молекул, проходящих за 1с через рассматриваемую площадку S, и увеличивает изменение скорости du упорядоченного движения. Так как , , то

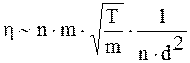; .         (16. 12)

Согласно (16. 12) коэффициент вязкости возрастает с температурой.

Коэффициент вязкости, рассмотренный нами, строго говоря, является коэффициентом сдвиговой вязкости . При перемещении пластинки в жидкости приходится затрачивать энергию на преодоление сил внутреннего трения, при этом энергия превращается в кинетическую энергию перемещения слоев газа, а затем – во внутреннюю энергию. При наличии всестороннего сжатия – растяжения, имеющего место при распространении звуковой волны, возможен и другой механизм перехода механической энергии во внутреннюю энергию. Сущность его состоит в перераспределении энергии между внешними (поступательными и вращательными) и внутренними (колебательными) степенями свободы молекул. Этот механизм получил название кнезеровского (по имени Кнезера – ученого, впервые предложившего его). В звуковой волне часть энергии-волны переходит на внутримолекулярные уровни, а затем рассеивается в виде тепла (повышения внутренней энергии).

Поскольку происходит перекачка энергии, диссипация энергии звуковой волны за сет данного механизма, то помимо сдвиговой вязкости вводят в рассмотрение и так называемую «объемную» вязкость .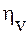

Полная или «эффективная» вязкость h равна

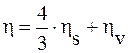.                              (16. 13)

В таком виде рассматривается вязкость в системе уравнений газовой динамики и гидродинамики.

Необходимо учитывать и то обстоятельство, что при быстропеременных процессах (к каким относится распространение упругих колебаний) указанные параметры проявляют зависимость от частоты :

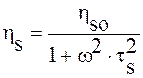; ,             (16. 14)

где 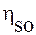 и  – статические значения сдвиговой и объемной вязкости;

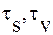 – времена релаксации сдвиговой и объемной вязкости.

 

16. 2. Диффузия и теплопроводность. Коэффициенты диффузии и теплопроводности

Диффузия - процесс взаимного проникновения молекул (атомов) постороннего вещества, обусловленный их тепловым движением. Диффузия всегда сопровождается переносом массы вещества. Она характерна для газов, жидкостей и твердых тел.

Самодиффузия - процесс взаимного проникновения собственных молекул (атомов), обусловленный их тепловым движением.

Согласно закону, экспериментально установленному Фиком, количество вещества dM, перенесенного через площадку dS, за время dt ( первый закон Фика ) равно

,                                (16. 15)

где D - коэффициент диффузии. Коэффициент диффузии - физическая величина, числено равная массе переносимого вещества через единичную площадку в единицу времени при градиенте концентрации, равном единице;

dс/dz - скорость изменения (градиент) концентрации в направлении z;

" минус" - показывает, что масса переносится в направлении убывания концентрации данной компоненты.

Пользуясь молекулярно-кинетическими представлениями можно получить

.                     (16. 16)

Сравнив (16. 15) и (16. 16), для коэффициента диффузии, будем иметь

.                                         (16. 17)

Анализ соотношения (16. 17) показывает:

1) так как при постоянной плотности газа < v> ~ T^1/2, то и D ~ T^1/2;

2) при T = const < l> ~ 1/p, следовательно, и D ~ 1/p.

Процесс переноса энергии между контактирующими телами или двумя поверхностями одного и того же тела, возникающий из-за разности температур называется теплопроводностью.

Одной из характеристик теплопроводности является тепловой поток. Тепловой поток - физическая величина, которая показывает, какое количество тепла, переносится в единицу времени через площадь dS при градиенте температуры dT/dz

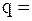
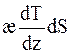.                                (16. 18)

Экспериментально Фурье установил закон теплопроводности, согласно которому количество тепла dQ, перенесенное через площадку dS за время dt, равно

,                           (16. 19)

где æ - коэффициент теплопроводности. Коэффициент теплопроводности - физическая величина, которая показывает, какое количество тепла, переносится через единичную площадку, в единицу времени при градиенте температур равном единице;

dT/dz - скорость изменения (градиент) температуры в направлении z.

Количество тепла перенесенного через ту же площадку dS за время dt, полученное из молекулярно-кинетических представлений, определяется соотношением

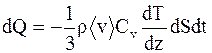.                    (16. 20)

Сравнение выше записанных выражений (16. 19 и 16. 20) позволяет установить формулу для коэффициента теплопроводности

 или 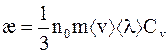. (16. 21)

Из формулы (16. 21) видно, что коэффициент теплопроводности не зависит от давления.

Между коэффициентами теплопроводности, диффузии и вязкости существует связь

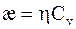; h = Dr; .             (16. 22)

Из выше рассмотренных положений, характерных для явлений переноса, видно, что все три коэффициента h, æ, D зависят от < l>. Определив какой-либо из коэффициентов можно вычислить < l>, а зная < l> - диаметр молекулы газа. Определенные таким методом значения диаметров молекул газа называют газокинетическими.

Надо еще раз отметить, что механизмы всех рассмотренных кинетических явлений характерны для газов, жидкостей и твердых тел.

Полученные результаты рассмотренных явлений переноса представлены в табл. 16. 1.

⇐ Предыдущая14151617181920212223Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: