 |
17.11.5. Скорость звука в кристалле. Цепочечная модель
|
|
|
|
17. 11. 5. Скорость звука в кристалле. Цепочечная модель
Попытаемся установить факторы, влияющие на скорость распространения звуковых волн в кристалле, основываясь на так называемой цепочной модели.
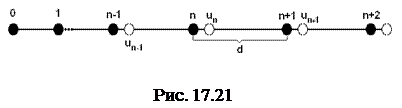Пусть кристалл имеет кубическую решетку. Рассмотрим цепочку атомов, проходящую через ребро какой-либо элементарной кристаллической ячейки (рис. 17. 21).
Положение равновесия атомов находятся на одном и том же расстоянии друг от друга – d (период кристаллической решетки, период идентичности). Массы атомов одинаковы и равны ma. В результате распространения звука в кристалле будут происходить упругие колебания твердого тела, которые в свою очередь обусловлены смещением частиц из положения равновесия. Эти механические смещения накладываются на беспорядочные тепловые колебания частиц.
Смещение частиц из положения равновесия можно представить в виде,
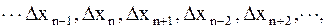
где индекс означает номер частицы.
В данной модели предполагается, что каждая молекула взаимодействует только с двумя соседями по цепочке, с молекулами из ближайших цепочек взаимодействия нет. При смещении частицы из положения равновесия, на неё со стороны ближайших соседей по цепочке действует сила, стремящаяся вернуть её в положение равновесия. При небольших по величине смещениях эта сила имеет полное сходство с упругой и, следовательно, должен выполнить закон Гука (упругая сила пропорциональна смещению частицы)
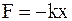, (17. 84)
где F – сила, действующая на данную частицу со стороны одной из соседних частиц.
k - коэффициент пропорциональности (коэффициент квазиупругой силы).
Можно записать дифференциальное уравнение
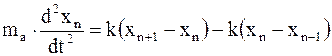; (17. 85)
|
|
|
; (17. 86)
или
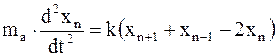; (17. 87)
Поскольку предполагается, что в кристалле в направлении цепочки распространяется звуковая волна, то воспользуемся выражением для смещения частиц (уравнением волны)
, (17. 88)
где kx – запаздывание по фазе частиц, находящихся на расстоянии x от источника звука, по отношению к частицам, непосредственно граничащим с источником.
С точки зрения первый слева (n = 0) в цепочке атом (х = 0) имеет нулевое запаздывание по фазе, второй (n = 1) отстает от него по фазе на d, третий (n = 2) на 2d, … n-й на nd. Поэтому для смещения из равновесия n-го атома (молекулы) можно записать
. (17. 89)
Сравнивая (17. 88) и (17. 89), получим
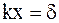. (17. 90)
Подставим выражение (17. 89) в (17. 89)
-mаω 2x0cos(ω t-nδ ) = kxo{cos[(ω t-nδ )- δ ]+
+cos[(ω t-nδ )+δ ]-2cos(ω t-nδ )}. (17. 91)
Воспользуемся тригонометрическим тождеством
cos(α +β )= cosα × cosβ -sinα × sinβ,
на основание которого получим
(17. 92)
Длина звуковой волны λ значительно превосходит период кристаллической решетки d, тогда δ < < 2p, так как разность фаз 2p набегает на расстоянии, равном длине волны. С учетом этого выражение (17. 93) принимает вид
-maω 2 = k{2cosδ -2} или +maω 2=2k{cosδ -1}. (17. 93)
Воспользовавшись тригонометрическим тождеством
,
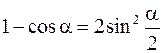преобразуем выражение (17. 93)
.
Откуда следует
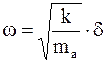. (17. 94)
Так как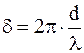 
, то (17. 94) преобразуется к виду
.
С другой стороны, скорость распространения волны v, частота колебаний n, длина волны λ связаны между собой соотношением 
, поэтому получаем
. (17. 95)
Таким образом, скорость распространения звука в кристалле зависит от коэффициента квазиупругой силы k, который в свою очередь определяется жесткостью межмолекулярных связей, массы молекулы (атома), периода кристаллической решетки d. Чем сильнее возрастают силы межмолекулярного взаимодействия, при смещении молекулы из положения равновесия, тем больше параметр k и тем больше скорость звука. Наоборот, с утяжелением частиц усиливаются инертные свойства среды, а скорость звука согласно (17. 95) становится меньше. Чем меньше d, тем более плотноупакованной является кристаллическая решетка, согласно (17. 95) при этом скорость будет уменьшаться.
|
|
|
Не надо забывать, что выражение (17. 95) для скорости звука в кристаллах получено для модели, которая, конечно, существенно отличается от реального объекта. Поэтому нельзя требовать от этого соотношения хорошего количественного согласия с опытом. Для нас важно, что соотношение (17. 95) показывает большую роль, которую играют в распространении упругих волн молекулярные параметры, структура вещества.
В заключение отметим, что измерение скорости распространения звуковых волн в кристаллических твердых телах дает полезную информацию о кристаллическом состоянии, и что звуковые волны в кристаллах используются для реализации не разрушающегося метода контроля (дефектоскопии).
БИБЛИОГРАФИЧЕСКИЙ СПИСОК
|
|
|
