 |
Квантовая механика
|
|
|
|
41. Найти длину волны де Бройля для электрона, прошедшего ускоряющее напряжение 106 В. Учесть релятивистские эффекты.
42. Найти длину волны де Бройля для электрона с энергией 1 МэВ.
43. Найти длину волны де Бройля для электрона в атоме водорода, движущегося по первой боровской орбите.
44. Найти период обращения электрона по первой боровской орбите в атоме водорода.
45. Определите первый потенциал возбуждения атома водорода.
46. Какую наименьшую скорость должны иметь электроны, чтобы в результате их столкновений с атомами водорода возбуждались линии всех серий спектра водорода?
47. Пользуясь теорией Бора, определите орбитальный магнитный момент электрона.
48. В спектре атома водорода интервал между первыми двумя линиями серии Бальмера составляет Dl = 1, 71× 10 – 7 м. Определите постоянную Ридберга.
49. Головные линии серий Лаймана и Бальмера различаются по
длине волны на Dl = 534, 7 нм. На основании этих данных определите постоянную Ридберга.
50. Определите спектральный диапазон, занимаемый серией Бальмера в спектре излучения атома водорода.
51. Какие спектральные линии появятся при возбуждении атома
водорода электроном с энергией 10, 2 эВ?
52. Пользуясь принципом неопределённости, найти приближённое выражение наименьшей энергии микрочастицы массой m в потенциальной яме шириной a с бесконечно высокими стенками.
53. Определить радиус a0 первой боровской орбиты и скорость электрона u на ней. Какова напряженность поля ядра на первой орбите?
54. Определить, во сколько раз увеличится радиус орбиты электрона у атома водорода, находящегося в основном состоянии, при возбуждении его квантом с энергией 12, 09 эВ.
|
|
|
55. Атомарный водород, возбуждаемый некоторым монохроматическим источником света, испускает только три спектральные линии. Определить квантовое число энергетического уровня, на который переходят возбужденные атомы, а также длины волн испускаемых линий.
56. Какова величина тока, соответствующего движению электрона на n-й орбите атома водорода?
57. Вычислить длину волны электрона, прошедшего ускоряющую разность потенциалов 500 кВ. Учесть зависимость массы от скорости.
58. Сравнить длины волн электрона и протона, прошедших ускоряющую разность потенциалов U = 1000 В.
59. Найти длину волны де Бройля для электронов, прошедших разность потенциалов 1 В, 100 В, 1000 В.
60. Найти длину волны: 1) электрона, летящего со скоростью 108 см/с; 2) атома водорода, движущегося со скоростью, равной средней квадратичной скорости при температуре 300 К; 3) шарика массой 1 г, движущегося со скоростью 1 см/с.
61. Получить в общем виде формулу, выражающую зависимость волны де Бройля от ускоряющего потенциала для релятивистской частицы.
62. Определить дебройлевскую длину волны движущегося электрона, если известно, что масса его на 1 % больше массы покоя.
63. При каком значении кинетической энергии дебройлевская длина волны электрона равна его комптоновской длине волны?
64. Параллельный поток моноэнергетических электронов падает нормально на диафрагму с узкой прямоугольной щелью шириной b = 1, 0 мкм. Определить скорость этих электронов, если на экране, отстоящем от щели на расстояние 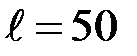 см, ширина центрального дифракционного максимума Dx = 0, 36 мм.
см, ширина центрального дифракционного максимума Dx = 0, 36 мм.
65. При движении вдоль оси ОХ скорость оказывается заданной с точностью Dux = 1 см/с. Оценить неопределенность координаты Dx:
а) для электрона; б) для броуновской частицы массой m » 10 – 13 г; в) для дробинки массой m » 0, 1 г.
66. Электрон пролетел ускоряющую разность потенциалов 105 В. Сравнить дебройлевскую длину волны частицы с величиной неопределенности в определении ее координаты, если относительная погрешность в определении импульса составляет 1 %.
|
|
|
67. Использовав соотношение неопределенности, оценить минимальную энергию Emin которой может обладать частица массы m
находящаяся в бесконечно глубокой одномерной потенциальной яме
ширины a.
68. Оценить скорость движения электрона u в атоме водорода,
исходя из того, что радиус r атома имеет величину порядка 0, 1 нм. Сравнить со значением скорости движения электрона на первой боровской
орбите.
69. Сравнить дебройлевскую длину волны протона, ускоренного до потенциала 109 В, с величиной неопределенности его координаты, соответствующей неточности импульса в 0, 1 %.
70. Электрон находится в потенциальном ящике шириной 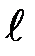 . В каких точках в интервале 0 < x <
. В каких точках в интервале 0 < x <  плотность вероятности нахождения электрона на первом и втором энергетических уровнях одинакова? Вычислить плотность вероятности для этих точек.
плотность вероятности нахождения электрона на первом и втором энергетических уровнях одинакова? Вычислить плотность вероятности для этих точек.
71. Электрон находится в одномерном потенциальном ящике шириной 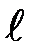 . Определить среднее значение координат < x > электрона в ящике.
. Определить среднее значение координат < x > электрона в ящике.
72. Найти вероятность прохождения электрона через прямоугольный потенциальный барьер при разности энергий U - E = 1 эВ, если
ширина ямы 0, 1 нм; 0, 5 нм.
73. Электрон проходит через прямоугольный потенциальный барьер ширины 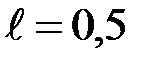 нм. Высота барьера U больше энергии E электрона на 1 %. Вычислить коэффициент прозрачности барьера D, если энергия электрона 10 эВ; 100 эВ.
нм. Высота барьера U больше энергии E электрона на 1 %. Вычислить коэффициент прозрачности барьера D, если энергия электрона 10 эВ; 100 эВ.
74. Ширина прямоугольного потенциального барьера d = 0, 2 нм. Разность энергий U - E = 1 эВ. Во сколько раз изменится вероятность прохождения электрона через барьер, если разность энергий возрастает в 100 раз?
75. Частица находится в основном состоянии (n = 1) в одномерном потенциальном ящике шириной а с абсолютно непроницаемыми стенками (0 < x < a). Найти вероятность пребывания частицы в областях 0 < x < a / 3 и a / 3 < x < 2 / 3a.
76. Пучок электронов с энергией E = 25 эВ встречает на своём пути потенциальный барьер высотой U = 9 эВ. Определить коэффициент отражения R и коэффициент пропускания D волн де Бройля для данного барьера.
77. Собственная функция 1s состояния атома водорода имеет вид 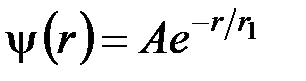 , где r1 – первый боровский радиус. Найти среднее значение радиуса и среднее значение потенциальной энергии атома в этом состоянии.
, где r1 – первый боровский радиус. Найти среднее значение радиуса и среднее значение потенциальной энергии атома в этом состоянии.
|
|
|
78. Пси-функция некоторой частицы имеет вид 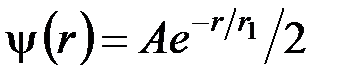 , где r –расстояние частицы от силового центра; А – константа. Найти:
, где r –расстояние частицы от силового центра; А – константа. Найти:
а) значение коэффициента А; б) среднее расстояние á rñ частицы от
центра.
79. Пси-функция некоторой частицы имеет вид:
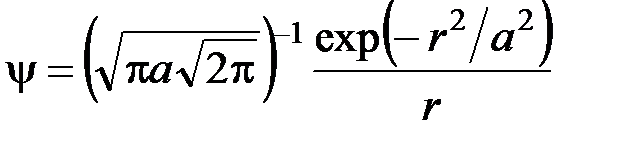
где r – расстояние частицы от силового центра; a – постоянная. Найти среднее расстояние á r ñ частицы от центра.
80. Пси-функция некоторой частицы имеет вид y = A exp (- r2 / 2 a2), где 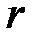 – расстояние частицы от силового центра; а – константа. Найти:
– расстояние частицы от силового центра; а – константа. Найти:
а) значение коэффициента А; б) наиболее вероятное и среднее расстояния частицы от центра.
|
|
|


