 |
Расстояние от точки до прямой в пространстве
|
|
|
|
Пусть задана прямая ℓ: 
и точка М0(х0, у0, z0) в О 
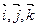. Прямая ℓ задана точкой М1(х1, у1, z1) и направляющим вектором 
(
). От точки М1 откладываем вектор = 
, при этом получим, что М2 Îℓ. На представителях векторов и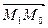 
строим параллелограмм, для которого легко можно найти площадь S и длину основания 
.
Так как при этом длина высоты параллелограмма есть искомое расстояние d, то получим:
r(М0, ℓ) = d = 
= 
= 
.
В координатной форме эта формула будет иметь вид:
r(М0, ℓ) = d = 
.
Расстояние между двумя прямыми в пространстве
Пусть в О 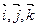заданы прямые
ℓ1: ,
ℓ2: 
.
Если прямые имеют хотя бы одну общую точку, то расстояние между ними полагаем равным нулю.
Если прямые параллельные, то для нахождения расстояния между ними выберем на одной прямой точку, например, М1(х1, у1, z1) Î ℓ1 и находим расстояние от точки М1(х1, у1, z1) до прямой ℓ2.
Рассмотрим случай, когда данные прямые скрещивающиеся. Из уравнений данных прямых получим: М1(х1, у1, z1) Î ℓ1 и () -направляющий вектор прямой ℓ1, М2(х2, у2, z2) Î ℓ2 и 
(
) -направляющий вектор прямой ℓ2. От точки М1 откладываем представители векторов и : 
, 
и достраиваем до параллелограмма М1АСВ. Далее, на основании М1АСВ и ребре М1М2 строим параллелепипед.
Так как прямые ℓ1 и ℓ2 лежат на основаниях построенного параллелепипеда, то расстояние между прямыми ℓ1 и ℓ2 можно найти как расстояние между параллельными плоскостями, содержащими основания параллелепипеда или как высоту d построенного параллелепипеда. Из формулы объема параллелепипеда находим
r(ℓ1; ℓ2) = d = 
= 
.
В координатной форме эта формула имеет вид:
r(ℓ1; ℓ2) = d = 
.
Взаимное расположение прямой и плоскости
|
|
|
Пусть прямая ℓ и плоскость p заданы в О 
уравнениями:
ℓ: 
p: 
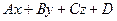= 0.
Для решения задачи решим систему уравнений, составленную из уравнений прямой и плоскости. Подставим в уравнение плоскости значения переменных из уравнений прямой
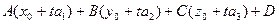= 0.
Находим: 
. (1)
1. Если 
¹ 0, то параметр t имеет единственное значение, подставляя которое в уравнения прямой получим координаты точки пересечения прямой и плоскости.
2. Если 
, то уравнение (1) не имеет решений, а, следовательно, прямая ℓ параллельна плоскости и не лежит на ней.
3. Если 
то уравнение (1) имеет множество решений, а, следовательно, прямая ℓ лежит на плоскости..
Следствие. Если вектор 
будет параллельным плоскости p: 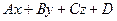= 0, то выполняется равенство:
.
Угол между прямой и плоскостью
Пусть прямая ℓ и плоскость p заданы в О 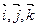уравнениями:
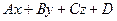ℓ: p: = 0.
Если прямая параллельна плоскости, то полагаем угол между ними равным 0. Если прямая ℓ и плоскость p пересекаются, то они имеют общую точку. От этой точки откладываем направляющий вектор прямой (
) и нормальный вектор плоскости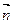 
(
).
Обозначим угол между прямой и плоскостью j, а угол между векторами и 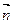обозначим a. Напоминаем, что углом между прямой и плоскостью является угол между прямой и ее проекцией на эту плоскость.
Между углами a и j простая зависимость:
j = 
Очевидно: sinj = |cosa|.
Так как
cosa = 
,
то
sinj = 
.
Пример 1. В прямоугольно-декартовой системе координат заданы вершины тетраэдра: А(-1; 2; 3), В(2; -2; 3), С(-1; 4; 5), D(-1; 6;0).
1. Составить а) параметрические уравнения прямой (А,В);
б) канонические уравнения прямой (В,С).
2. Составить уравнение прямой (B,D), как линии пересечения двух плоскостей.
3. Составить уравнение прямой, содержащей высоту [DH] тетраэдра ABCD и найти координаты точки H.
4. Найти косинус угла между прямыми (А,В) и (В,С).
5. Найти синус угла между прямой (B,D) и плоскостью (АВС).
Решение
1. а) Прямую (А,В) можно задать точкой А(-1; 2; 3) и вектором 
, тогда ее уравнение в параметрической форме можно составить следующим образом:
|
|
|
где 
|R.
б) Прямую (В,С) зададим точкой В(2; -2; 3) и вектором 
. Находим канонические уравнения этой прямой:
.
2. Прямая (B,D) является линией пересечения плоскостей (ABD) и (CBD). Ранее мы находили уравнения этих плоскостей (см. пример § 3)
(ABD): 4x + 3y + 4z − 14 = 0,
(BCD): 34x + 15y + 6z – 56 = 0.
Поэтому имеем общее уравнение прямой (B,D):
(B,D): 
3. Прямую (DH) можно задать точкой D(-1; 6; 0) и направляющим вектором 
, который является нормальным к плоскости (АВС). Ранее мы находили уравнение этой плоскости (АВС): 4х+ 3у -3z +7= 0. (см. пример § 3). Из уравнения находим координаты нормального вектора 
.
Тогда канонические уравнения прямой (D,H) будут иметь следующий вид:
.
4. Пусть 
и 
- направляющие векторы прямых (А,В) и (В,С), соответственно. Обозначим j – угол между векторами и , а a – острый угол между прямыми (А,В) и (В,С). Тогда либо a = j, либо a = p − j.
Поэтому cosa = |cosj|.
Так как
,
то, учитывая, что 
, получим
Итак, 
5)
Ранее мы получили формулу для вычисления угла между прямой и плоскостью
|
sinj = , где (
) – координаты направляющего вектора прямой (В,D), а (А,В,С) – координаты нормального вектора 
данной плоскости.
Так как
, (АВС): 4х+ 3у -3z +7=0, (4,3,-3),
то получим:
Итак,
.
Пример 2. В прямоугольно-декартовой системе координат заданы точки: А(-1; 0; 3), В(2; -2; 0), С(-1; 1; 1), D(-1; 6;0).
1. Найти расстояние от точки А до прямой (D,С).
2. Найти расстояние между прямыми (А,В) и (D,С).
Решение. 1. Прямая (D,С) задается точкой D и направляющим вектором 
, при этом D(-1; 6;0), (0, -5, 1), 
(0, -6, 3). Ранее мы получили формулу для вычисления расстояния
r 
= 
.
Так как [ 
] = 
= 
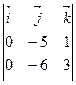(-15+6) = −9 , то
|[ ]| = 9.
С другой стороны,
| | = 
.
Поэтому
r = 
.
2. Прямая (А,В) задается точкой А и вектором 
, а прямая (D,С) задается точкой D и направляющим вектором , при этом А(-1; 0; 3), (3, -2, -3), D(-1; 6;0), (0, -5, 1), (0, -6, 3). Ранее мы получили формулу для вычисления расстояния
r((А,В); (D,C)) = 
.
(
) = 
= 3 (-1)3 
= − 27,
|()| = 27.
Так как
[ 
] = 
= (−6−15) − 
(9) + 
(−15) = −21 – 9 – 15 , то
|[ ]| = 
= 
≈27,33.
Следовательно, r((А,В); (D,C)) ≈ 
≈ 0,987.
|
|
|
