 |
Методика решения иррациональных уравнений
|
|
|
|
В работе будем придерживаться следующего определения иррационального уравнения:
Иррациональным уравнением называется уравнение, содержащее неизвестное под знаком корня.
Прежде чем приступить к решению сложных уравнений учащиеся должны научиться решать простейшие иррациональные уравнения. К простейшим иррациональным уравнениям относятся уравнения вида:
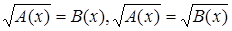
Основная идея решения иррационального уравнения состоит в сведении его к рациональному алгебраическому уравнению, которое либо равносильно исходному иррациональному уравнению, либо является его следствием.
Главный способ избавиться от корня и получить рациональное уравнение - возведение обеих частей уравнения в одну и ту же степень, которую имеет корень, содержащий неизвестное, и последующее "освобождение" от радикалов по формуле  . [6]
. [6]
Если обе части иррационального уравнения возвести в одну и ту же нечетную степень и освободиться от радикалов, то получится уравнение, равносильное исходному. [6]
При возведении уравнения в четную степень получается уравнение, являющееся следствием исходного. Поэтому возможно появление посторонних решений уравнения, но не возможна потеря корней. Причина приобретения корней состоит в том, что при возведении в четную степень чисел, равных по абсолютной величине, но разных по знаку, получается один и тот же результат.
Так как могут появиться посторонние корни, то необходимо делать проверку, подставляя найденные значения неизвестной только в первоначальное уравнение, а не в какие-то промежуточные.
Рассмотрим применение данного метода решения иррациональных уравнений. [7]
Пример 1. Решите уравнение  .
.
|
|
|
Решение. Возведем обе части этого уравнения в квадрат  и получим
и получим 

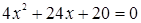

 , откуда следует, что
, откуда следует, что  или
или 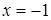 .
.
Проверка.  :
: 
 . Это неверное числовое равенство, значит, число
. Это неверное числовое равенство, значит, число  не является корнем данного уравнения.
не является корнем данного уравнения.
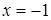 :
:  . Это верное числовое равенство, значит, число
. Это верное числовое равенство, значит, число  является корнем данного уравнения.
является корнем данного уравнения.
Ответ. 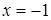 .
.
Проверка, осуществляемая подстановкой найденного решения в исходное уравнение, может быть легко реализована, если проверяемые корни - "хорошие" числа, а для "громоздких" корней проверка может быть сопряжена со значительными вычислительными трудностями. Поэтому каждый образованный школьник должен уметь решать иррациональные уравнения с помощью равносильных преобразований, так как, выполняя равносильные преобразования, можно не опасаться ни потери корней, ни приобретения посторонних решений. [17] Аккуратное возведение в четную степень уравнения вида  состоит в переходе к равносильной ему системе
состоит в переходе к равносильной ему системе

Неравенство  в этой системе выражает условие, при котором уравнение можно возводить в четную степень, отсекает посторонние решения и позволяет обходиться без проверки. [17]
в этой системе выражает условие, при котором уравнение можно возводить в четную степень, отсекает посторонние решения и позволяет обходиться без проверки. [17]
Школьники довольно часто добавляют к этой системе неравенство 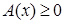 . Однако этого делать не нужно и даже опасно, поскольку условие
. Однако этого делать не нужно и даже опасно, поскольку условие  автоматически выполняется для корней уравнения
автоматически выполняется для корней уравнения  , в правой части которого стоит неотрицательное выражение. [9]
, в правой части которого стоит неотрицательное выражение. [9]
Пример 2. Решить уравнение  .
.
Решение. Это уравнение равносильно системе
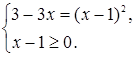
Решая первое уравнение этой системы, равносильное уравнению  , получим корни
, получим корни  и
и  .
.
Второй корень не удовлетворяет неравенству системы и, следовательно, является посторонним корнем исходного уравнения.
Ответ.  .
.
При решении иррациональных уравнений полезно перед возведением обеих частей уравнения в некоторую степень "уединить радикал", то есть представить уравнение в виде  .
.
Тогда после возведения обеих частей уравнения в n- ую степень радикал справа исчезнет. [4]
|
|
|
Пример 3. Решить уравнение 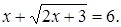
Решение. Метод уединения радикала приводит к уравнению  . Это уравнение равносильно системе
. Это уравнение равносильно системе

Решая первое уравнение этой системы, получим корни 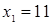 и
и 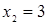 , но условие
, но условие  выполняется только для
выполняется только для  .
.
Ответ.  .
.
Полезно запомнить схему решения еще одного вида иррациональных уравнений  . Такое уравнение равносильно каждой из двух систем
. Такое уравнение равносильно каждой из двух систем

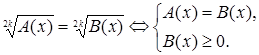
Поскольку после возведения в четную степень получаем уравнение-следствие  . Мы должны, решив его, выяснить, принадлежат ли найденные корни области определения исходного уравнения, то есть выполняется ли неравенство
. Мы должны, решив его, выяснить, принадлежат ли найденные корни области определения исходного уравнения, то есть выполняется ли неравенство 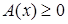 (или
(или 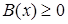 ). На практике из этих систем выбирают для решения ту, в которой неравенство проще. [9]
). На практике из этих систем выбирают для решения ту, в которой неравенство проще. [9]
Пример 4. Решить уравнение
 .
.
Решение. Это уравнение равносильно системе

Решая первое уравнение этой системы, равносильное уравнению  , получим корни
, получим корни  и
и  .
.
Однако при этих значениях x не выполняется неравенство  , и потому данное уравнение не имеет корней.
, и потому данное уравнение не имеет корней.
Ответ. Корней нет.
Теперь можно перейти к решению иррациональных уравнений, не относящихся к простейшим.
Пример 5. Решить уравнение  .
.
Решение. Возведем обе части уравнения в квадрат и произведем приведение подобных членов, перенос слагаемых из одной части равенства в другую и умножение обеих частей на  .
.
В результате получим уравнение
 , (1)
, (1)
являющееся следствием исходного.
Снова возведем обе части уравнения в квадрат. Получим уравнение
 ,
,
которое приводится к виду
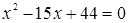 .
.
Это уравнение (также являющееся следствием исходного) имеет корни  ,
, 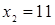 . Оба корня, как показывает проверка, удовлетворяют исходному уравнению.
. Оба корня, как показывает проверка, удовлетворяют исходному уравнению.
Ответ.  ,
, 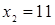 .
.
|
|
|


