 |
Методика решения иррациональных неравенств
|
|
|
|
Если в любом иррациональном уравнении заменить знак равенства на один из знаков неравенства: >, 
, <, 
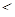, то получим иррациональное неравенство. [19] Поэтому под иррациональным неравенством будем понимать неравенство, в котором неизвестные величины находятся под знаком корня. [16]
Способ решения таких неравенств состоит в преобразовании их к рациональным неравенствам путем возведения обеих частей неравенства в степень.
Решение иррациональных неравенств осложняется тем обстоятельством, что здесь, как правило, исключена возможность проверки, поэтому надо стараться делать все преобразования равносильными.
При решении иррациональных неравенств следует запомнить правило: при возведении обеих частей неравенства в нечетную степень всегда получается неравенство, равносильное данному неравенству. [16]
Но если при решении уравнений в результате возведения четную степень мы могли получить посторонние корни (которые, как правило легко проверить) и не могли потерять корни, то корни неравенства при бездумном возведении в четную степень могут одновременно и теряться, и приобретаться. [8]
Например, возведя в квадрат:
верное неравенство 
, мы получим верное неравенство 
;
верное неравенство 
, мы получим неверное неравенство 
;
неверное неравенство 
, мы получим верное неравенство 
;
неверное неравенство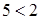 
, мы получим неверное неравенство 
.
Вы видите, что возможны все комбинации верных и неверных неравенств. [8]
Однако верно основное используемое здесь утверждение: если обе части неравенства возводят в четную степень, то получится неравенство, равносильное исходному только в том случае, если обе части исходного неравенства неотрицательны. [16]
|
|
|
Поэтому основным методом решения иррациональных неравенств является сведение исходного неравенства к равносильной системе или совокупности систем рациональных неравенств. [17]
Наиболее простые иррациональные неравенства имеют вид: [16], [17]
(или 
);
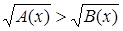(или 
);
(или 
).
Иррациональное неравенство 
(или 
) равносильно системе неравенств
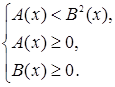или 
. {1}
Первое неравенство в системе {1} является результатом возведения исходного неравенства в степень, второе неравенство представляет собой условие существования корня в исходном неравенстве, а третье неравенство системы выражает условие, при котором это неравенство можно возводить в квадрат.
Иррациональное неравенство 
(или 
) равносильно совокупности двух систем неравенств
или 
. {2}
Обратимся к первой системе схемы {2}. Первое неравенство этой системы является результатом возведения исходного неравенства в квадрат, второе - условие, при котором это можно делать.
Вторая система схемы {2} соответствует случаю, когда правая часть отрицательна, и возводить в квадрат нельзя. Но в этом и нет необходимости: левая часть исходного неравенства - арифметический корень - неотрицательна при всех x, при которых она определена. Поэтому исходное неравенство выполняется при всех x, при которых существует левая часть. Первое неравенство второй системы и есть условие существования левой части.
Иррациональное неравенство 
(или 
) равносильно системе неравенств
или 
. {3}
Поскольку обе части исходного неравенства неотрицательны при всех x, при которых они определены, поэтому его можно возвести в квадрат. Первое неравенство в системе {3} является результатом возведения исходного неравенства в степень. Второе неравенство представляет собой условие существования корня в исходном неравенстве, понятно, что неравенство 
выполняется при этом автоматически.
|
|
|
Схемы {1}-{3} - наш основной инструмент при решении иррациональных неравенств, к ним сводится решение практически любой задачи. Разберем несколько примеров. [8]
Пример 1. Решить неравенство 
.
Решение. Заметим, что правая часто этого неравенства отрицательна, в то время как левая часть неотрицательна при всех значениях x, при которых она определена. Поэтому неравенство решений не имеет.
Ответ. Решений нет.
Пример 2. Решить неравенство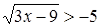 
.
Решение. Как и в предыдущем примере, заметим, что правая часть данного неравенства отрицательна, следовательно, возводить это неравенство в квадрат нельзя. И не надо, поскольку левая часть исходного неравенства неотрицательна при всех значениях x, при которых она определена. Это означает, что левая часть больше правой части при всех значениях x, удовлетворяющих условию 
.
Ответ. 
.
Пример 3. Решить неравенство 
.
Решение. В соответствии со схемой {1} решения неравенств этого типа, запишем равносильную ему систему рациональных неравенств
Условие 
выполнено при всех x, и нет необходимости добавлять его к выписанной системе.
Ответ.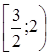 
.
Пример 4. Решить неравенство 
.
Решение. Это неравенство решается при помощи схемы {2}. В данном случае 
, поэтому можно сразу записать неравенство, равносильное исходному 
. Ответ. 
.
Пример 5. Решить неравенство 
.
Решение. Это неравенство может быть решено при помощи схемы {1}. Система, равносильная исходному неравенству, имеет вид
Ответ.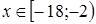 
.
Пример 6. Решить неравенство 
.
Решение. Данное неравенство можно решать с помощью схемы {2}. Оно равносильно совокупности двух систем
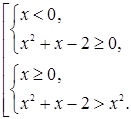
Ответ. 
.
Пример 7. Решить неравенство 
.
Решение. Согласно схеме {3}, данное неравенство равносильно системе
Ответ. 
Более сложно решение иррациональных неравенств вида
.
Поскольку 
, 
, то должны выполнятся условия 
, 
, 
(соответственно 
). На множестве, где эти условия выполняются, данное неравенство равносильно неравенству 
.
(соответственно неравенству 
), которое сводится к разобранным выше типам неравенств. [4]
Пример 8. Решить неравенство 
.
Решение. Данное неравенство равносильно следующей системе неравенств:
Последнее неравенство этой системы приводится к виду 
, откуда находим, что 
. Решение исходного неравенства является общей частью решений всех неравенств системы, т.е. имеет вид 
.
|
|
|
Ответ. 
.
Для решения иррациональных неравенств, так же как и для решения иррациональных уравнений, с успехом может применяться способ подстановки или введения новой переменной.
Весьма эффективны так называемые рационализирующие подстановки. Применение рационализирующих подстановок позволяет привести функцию, иррациональную относительно исходной переменной, к рациональной функции относительно новой переменной. [17]
Пример 9. Решить неравенство 
.
Решение. Введем новую переменную t с помощью рационализирующей подстановки 
, 
.
Тогда 
и для переменной t получаем рациональное неравенство
, где 
.
Ответ. 
.
Заключение
В данной курсовой работе сделана попытка разработать методику обучения решению иррациональных уравнений и неравенств в школе.
В ходе работы были решены следующие задачи:
Проанализированы действующие учебники алгебры и начала математического анализа для выявления представленной в них методики решения иррациональных уравнений и неравенств. Проведенный анализ позволяет сделать следующие выводы:
теория методов изложена не достаточно строго;
в одном учебнике [1] материала по методам решения иррациональных уравнений нет. В остальных учебниках рассмотрены два основных способа решения: возведение обеих частей уравнения в степень, с последующей подстановкой полученных корней в исходное уравнение, а также решение уравнений с помощью равносильных преобразований;
очень мало материала по методам решения иррациональных неравенств;
среди предлагаемых заданий много однотипных;
Изучены стандарты образования по данной теме;
Изучена учебно-методическая литература по данной теме;
Рассмотрены ситуации, связанные с потерей или приобретением посторонних корней в процессе решения, показано, как их распознавать и как с ними можно бороться;
Подобраны примеры решения иррациональных уравнений и неравенств для демонстрации излагаемого теоретического материала;
|
|
|
Показано, что общие методы решения уравнений применимы для решения иррациональных уравнений и неравенств.
Список библиографии
1. Алимов Ш.А. Алгебра и начала анализа: Учеб. для 10-11 кл. сред. шк. - М.: Просвещение, 1993. - 254 с.
2. Башмаков М.И. Алгебра и начала анализа: Учеб. для 10-11 кл. сред. шк. - М.: Просвещение, 1992. - 351 с.
3. Болтянский В.Г. Математика: лекции, задачи, решения. - Литва: Альфа, 1996. - 637 с.
4. Виленкин Н.Я. и др. Алгебра и математический анализ для 11 класса: Учеб. пособие для учащихся шк. и кл. с углубл. изуч. математики. - М.: Просвещение, 1998. - 288 с.
5. Галицкий М.Л. Сборник задач по алгебре для 8-9 классов: Учеб. пособие для учащихся шк. и кл. с углубл. изуч. математики. - М.: Просвещение, 1999. - 271с.
6. Григорьев А.М. Иррациональные уравнения. // Квант, №1, 1972, с.46-49.
7. Денищева Л.О. Готовимся к единому государственному экзамену. Математика. - М.: Дрофа, 2004. - 120 с.
8. Егоров А. Иррациональные неравенства. // Математика. Первое сентября, №15, 2002. - с.13-14.
9. Егоров А. Иррациональные уравнения. // Математика. Первое сентября, №5, 2002. - с.9-13.
10. Мордкович А.Г. Алгебра и начала анализа.10-11 кл.: В двух частях. Ч.1: Учеб. для общеобразоват. учреждений. - М.: Мнемозина, 2004. - 315 с.
11. Мордкович А.Г. Алгебра и начала анализа.10-11 кл.: В двух частях. Ч.2: Задачник для общеобразоват. учреждений. - М.: Мнемозина, 2004. - 315 с.
12. Мордкович А.Г. Кто-то теряет, кто-то находит. // Квант, №5, 1970, с.48-51.
13. Колмогоров А.Н. Алгебра и начала анализа. Учеб. для 10-11 кл. сред. шк. - М.: Просвещение, 1991. - 320 с.
14. Кузнецова Г.М. Программа для общеобразоват. школ, гимназий, лицеев: Математика.5-11 кл. - М.: Дрофа, 2004, 320 с.
15. Потапов М. Как решать уравнения без ОДЗ. // Математика. Первое сентября, №21, 2003. - с.42-43.
16. Соболь Б.В. Пособие для подготовки к единому государственному экзамену и централизованному тестированию по математике. - Ростов на Дону: Феникс, 2003. - 352 с.
17. Черкасов О.Ю. Математика: Справочник для старшеклассников и поступающих в вузы. - М.: АСТ-ПРЕСС, 2001. - 576 с.
18. Шабунин М. Лекции для абитуриентов. Лекция 1. // Математика. Первое сентября, №24, 1996. - с.24.
19. Шувалова Э.З. Повторим математику. Учеб пособ. для поступающих в вузы. - М.: Высшая школа, 1974. - 519 с.
|
|
|
