 |
Применение общих методов для решения иррациональных уравнений
|
|
|
|
1. Метод разложения на множители.
Суть этого метода заключается в следующем: уравнение 
можно заменить совокупностью уравнений:
; 
; 
.
Решив уравнения этой совокупности, нужно взять те их корни, которые принадлежат области определения исходного уравнения, а остальные отбросить как посторонние. Приведем пример применения метода разложения на множители при решении иррациональных уравнений. [10]
Пример 11. Решите уравнение 
.
Решение. Для решения таких уравнений следует пользоваться правилом расщепления:
Произведение равно нулю тогда и только тогда, когда хотя бы один из входящих в него сомножителей равен нулю, а остальные при этом имеют смысл. [ 17]
Первый множитель равен нулю при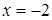 
, но тогда второй множитель потеряет смысл, так как при 
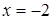он равен 
. Значит, 
решением данного уравнения быть не может.
Второй множитель равен нулю при 
или 
. Первый множитель определен для всех действительных чисел, значит, и могут быть решениями данного уравнения. Ответ. , 
2. Метод введения новой переменной.
Мощным средством решения иррациональных уравнений является метод введения новой переменной, или "метод замены". Метод обычно применяется в случае, если в уравнении неоднократно встречается некоторое выражение, зависящее от неизвестной величины. Тогда имеет смысл обозначить это выражение какой-нибудь новой буквой и попытаться решить уравнение сначала относительно введенной неизвестной, а потом уже найти исходную неизвестную. В ряде случаев удачно введенные новые неизвестные иногда позволяют получить решение быстрее и проще; иногда же без замены решить задачу вообще невозможно. [6], [17]
Пример 12. Решить уравнение 
.
|
|
|
Решение. Положив 
, получим существенно более простое иррациональное уравнение 
. Возведем обе части уравнения в квадрат:
.
Далее последовательно получаем:
;
;
;
;
, 
.
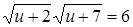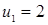Проверка найденных значений их подстановкой в уравнение 
показывает, что 
- корень уравнения, а 
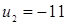- посторонний корень.
Возвращаясь к исходной переменной x, получаем уравнение 
, т.е. квадратное уравнение 
, решив которое находим два корня: 
, 
.
Ответ: 
, 
.
Замена особенно полезна, если в результате достигается новое качество, например, иррациональное уравнение превращается в квадратное.
Пример 13. Решить уравнение 
.
Решение. Перепишем уравнение так: 
.
Видно, что если ввести новую переменную 
, то уравнение примет вид 
, откуда 
, 
.
Теперь задача сводится к решению уравнения 
и уравнения 
. Первое из этих решений не имеет, а из второго получаем 
, 
.
Ответ.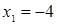 
, 
.
Отметим, что "бездумное" применение в Примере 11 метода "уединения радикала" и возведение в квадрат привело бы к уравнению четвертой степени, решение которого представляет собой в общем случае чрезвычайно сложную задачу.
Пример 14. Решить уравнение
.
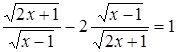Введем новую переменную
, 
.
Исходное уравнение принимает вид
,
откуда учитывая ограничение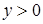 
, получаем 
. Тогда 
.
Ответ. 
.
Уравнения вида 
(здесь a, b, c, d - некоторые числа, m, n - натуральные числа, обычно не превосходящие 4) и ряд других уравнений часто удается решить при помощи введения двух вспомогательных неизвестных и последующего перехода к рациональной системе. [17]. Пример 15. Решить уравнение 
.
Решение. Введем новые переменные
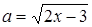и 
.
Тогда исходное уравнение принимает вид: 
. Полученное уравнение обладает одним существенным недостатком: в нем две неизвестных. Но заметим, что величины a и b не являются независимыми переменными - они зависят одна от другой посредством старой переменной x. Выразим x через a и b
|
|
|
и 
.
Теперь, можно заметить, что если первое уравнение умножить на два и затем вычесть из него второе, то переменная x исключается, и остается связь только между a и b
.
В результате получаем систему двух уравнений относительно двух неизвестных a и b
Решая эту систему методом подстановки, приходим к уравнению 
, корнями которого являются числа 
и 
. Корень 
посторонний, поскольку 
. Осталось решить уравнение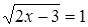 
, откуда находим 
.
Ответ. 
.
Пример 16. Решить уравнение
. [6]
Решение. Возведение обеих частей этого уравнения в четвертую степень не обещает ничего хорошего. Если же положить 
, 
, то исходное уравнение переписывается так: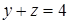 
. Поскольку мы ввели две новые неизвестные, надо найти еще одно уравнение, связывающее y и z.
Для этого возведем равенства 
, 
в четвертую степень и заметим, что 
.
Итак, надо решить систему уравнений
она имеет два (действительных) решения: 
, 
; 
, 
. Остается решить систему двух уравнений с одним неизвестным
и систему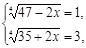 
первая из них дает 
, вторая дает 
.
Ответ. 
, 
.
Не всегда после введения новых переменных удается исключить неизвестную x, как это было в рассмотренных Примерах 15, 16. Однако, как можно убедиться из следующего примера, переход от уравнения к системе может помочь и в таком случае. [17]
Пример 17. Решить уравнение
.
Решение. Введем новые переменные
и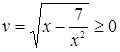 
.
По стандартной схеме получим следующую систему уравнений:
откуда следует, что
.
Так как 
, то u и v должны удовлетворять системе
из которой после несложных преобразований получаем уравнение
.
Заметим, что это уравнение имеет корень 
. Тогда, разделив многочлен на 
, получаем разложение левой части уравнения на множители
.
Отсюда следует, что 
- единственное решение этого уравнения. После проверки записываем это решение в ответ.
Ответ.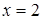 
3. Тригонометрическая замена.
Иногда подходящей заменой неизвестной иррациональное уравнение можно свести к тригонометрическому уравнению. При этом полезными могут оказаться следующие замены переменной. [17]
Если в уравнение входит радикал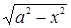 
, то можно сделать замену 
, 
или 
, 
.
Если в уравнение входит радикал 
, то можно сделать замену 
tg t, 
или 
ctg t, 
.
|
|
|
Если в уравнение входит радикал 
, то можно сделать замену 
, или 
, .
Проиллюстрируем использование этих замен на следующих примерах.
Пример 18. Решить уравнение 
.
Решение. В данное уравнение входит выражение 
, поэтому в соответствии с пунктом 2, сделаем замену
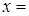tg t, где 
.
Тогда выражение 
, входящее в уравнение, можно преобразовать
и исходное уравнение можно записать в виде
.
Поскольку 
не равен нулю при рассматриваемых значениях t, то полученное уравнение равносильно уравнению
.
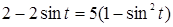Решая это уравнение, находим два возможных значения
и 
.
Из всех корней этих уравнений промежутку принадлежит единственное значение 
.
Поэтому соответствующее значение x равно
.
Ответ. 
.
Пример 19. Решить уравнение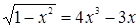 
.
Решение. В этом уравнении x по ОДЗ может принимать только значения из отрезка 
, что приводит к мысли совершить замену
, где 
.
В результате такой замены приходим к уравнению
.
Учтем, что 
и 
, получим уравнение 
.
В силу ограничения выполнено 
, поэтому приходим к уравнению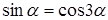 
, которое, пользуясь формулой приведения, сведем к стандартному виду
.
Решая последнее уравнение, находим
или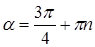 
, 
.
Условию удовлетворяют лишь три значения
, 
, 
. Поэтому
, 
, 
.
Ответ. , , 
.
4. Умножение обеих частей уравнения на функцию.
Иногда иррациональное уравнение удается решить довольно быстро, если обе его части умножить на удачно подобранную функцию. Конечно, при умножении обеих частей уравнения на некоторую функцию могут появиться посторонние решения, ими могут оказаться нули самой этой функции. Поэтому предлагаемый метод требует обязательного исследования получающихся значений. [6]
Пример 20. Решить уравнение 
.
Решение. Умножим обе части уравнения на одну и ту же функцию 
. Выражение 
называется сопряженным для выражения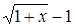 
. Цель такого умножения ясна: использовать тот факт, что произведение двух сопряженных выражений уже не содержит радикалов.
|
|
|
В результате этого умножения и очевидных преобразований приходим к уравнению
.
Оно имеет единственный корень 
, так как уравнение 
решений не имеет.
Подстановка в исходное уравнение показывает, что 
- корень.
Ответ. .
Впрочем, здесь можно было обойтись и без подстановки: функция 
нигде в нуль не обращается, и поэтому умножение обеих частей уравнения 
на эту функцию не приводит к появлению посторонних решений.
Пример 21. Решить уравнение 
. [9]
Решение. Умножим обе части уравнения на функцию 
. После преобразований получим уравнение
.
Оно имеет два корня: 
. Проверка показывает, что 
- посторонний корень (нетрудно видеть, - корень функции ). Таким образом, уравнение имеет единственный корень 
.
Ответ. .
|
|
|
