 |
Тождественные преобразования при решении иррациональных уравнений
|
|
|
|
При решении иррациональных уравнений и неравенств часто приходится применять тождественные преобразования, связанные с использованием известных формул. К сожалению, эти действия иногда столь же небезопасны, как уже рассмотренное возведение в четную степень, - могут приобретаться или теряться решения. [17]
Обсудим несколько ситуаций, в которых эти проблемы наступают, и посмотрим, как их распознать и как можно с ними бороться.
I. Пример 6. Решить уравнение 
.
Решение. При первом же взгляде на это уравнение возникает мысль избавиться от корня с помощью "преобразования" 
.
Но это неверно, так как при отрицательных значениях x оказывалось бы, что 
.
Необходимо запомнить формулу 
. Уравнение теперь легко решается
.
Ответ. 
.
Теперь посмотрим "обратное" преобразование.
Пример 7. Решить уравнение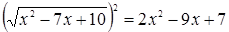 
.
Решение. Сейчас настало время задуматься о безопасности формулы
.
Нетрудно видеть, что ее левая и правая части имеют разные области определения и что это равенство верно лишь при условии 
. Поэтому исходное уравнение равносильно системе
Ответ. 
.
II. Следующее преобразование, которое должно явиться предметом заботы для каждого, кто решает иррациональные уравнения, определяется формулой
.
Если пользоваться этой формулой слева направо, расширяется ОДЗ и можно приобрести посторонние решения. Действительно, в левой части обе функции 
и 
должны быть неотрицательны; а в правой неотрицательным должно быть их произведение. [17]
Замечание. При возведении уравнения в квадрат учащиеся нередко в уравнении типа (1) из Примера 5 производят перемножение подкоренных выражений, т.е. вместо такого уравнения пишут уравнение
|
|
|
.
Такое "склеивание" не приводит к ошибкам, поскольку такое уравнение является следствием уравнения (1). Следует, однако, иметь в виду, что в общем случае такое перемножение подкоренных выражений дает неравносильные уравнения. Поэтому в рассмотренном выше примере можно было сначала перенести один из радикалов в правую часть уравнения, т.е. уединить один радикал. Тогда в левой части уравнения останется один радикал, и после возведения обеих частей уравнения в квадрат в левой части уравнения получится рациональное выражение. [3]
Пример 8. Решить уравнение
.
Решение. Уединив первый радикал, получаем уравнение
,
равносильное исходному.
Возводя обе части этого уравнения в квадрат, получаем уравнение
,
равносильное уравнению
. (2)
Уравнение (2) является следствием исходного уравнения. Возводя обе части этого уравнения в квадрат, приходим к уравнению
, или 
.
Это уравнение является следствием уравнения (2) (а значит, и исходного уравнения) и имеет корни 
, 
.
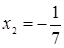Первый корень удовлетворяет исходному уравнения, а второй - не удовлетворяет.
Ответ. 
.
Рассмотрим пример, где реализуется проблема с "расклеиванием" корней, то есть использование формулы 
. [13]
Пример 9. Решить уравнение 
.
Решение. Попробуем решить это уравнение разложением на множители
.
Заметим, что при этом действии оказалось потерянным решение 
. Посмотрите, оно подходит к исходному уравнению и уже не подходит к полученному: 
не имеет смысла при 
. Поэтому это уравнение лучше решать обычным возведением в квадрат
Ответ. 
, 
.
Вывод. Есть два пути. Или аккуратно возводить уравнение в квадрат, или безошибочно определять, какие решения могли быть потеряны, и проверить, не случилось ли этого на самом деле.
III. Существует еще более опасное действие - сокращение на общий множитель. [17]
|
|
|
Пример 10. Решить уравнение 
.
" Решение". Сократим обе части уравнения на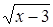 
, получим
.
Нет ничего более опасного и неправильного, чем это действие. Во-первых, подходящее решение исходного уравнения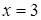 
было потеряно; во-вторых, было приобретено два посторонних решения 
. Получается, что новое уравнение не имеет ничего общего с исходным! Вот правильное решение.
Решение. Перенесем все члены в левую часть уравнения и разложим ее на множители
.
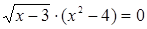Это уравнение равносильно системе
которая имеет единственное решение 
.
Ответ. .
|
|
|
