14.2. Основы цветовых измерений

Мы рассмотрели некоторые моменты, касающиеся природы цветового ощущения, зрительного аппарата, цветового зрения и субъективных характе­ристик цвета. Они нам понадобятся в дальнейшем для лучшего понимания конкретных вопросов цветовых измерений. Ведь для того, чтобы создать стройную колориметрическую систему измерения цвета, надо учесть субъек­тивизм восприятия цвета, а также формализовать в математической форме свойства зрительной системы глаза человека, перейдя от субъективных харак­теристик цвета к научному, изложенному языком цифр и формул, строгому математическому описанию. Обратимся теперь непосредственно к рассмотре­нию основ колориметрии, т. е. метрологии цвета.

Цветовые законы Грассмана. Итак, обращаясь к основным ощущени­ям, введем по аналогии понятие основных излучений или основных цветов. Иногда в литературе их еще называют цветовыми стимулами.

Под основными излучениями или цветами в колориметрии пони­маются цвета, подчиняющиеся трем законам аддитивного синтеза цветов, впервые сформулированным в 1853 году немецким ученым Германом Грассманом [66-68].

1. Первый закон Грассмана (закон трехмерности). Любой цвет однозначно выражается тремя цветами, если они линейно независимы, т. е. ни один из них нельзя получить путем сложения двух остальных цветов. Закон утверждает возможность описания цвета с помощью цветовых уравнений.

2. Второй закон Грассмана (закон непрерывности). При непрерывном из­менении излучения цвет смеси также меняется непрерывно. Не существует такого цвета, к которому нельзя было бы подобрать бесконечно близкий.

3. Третий закон Грассмана (закон аддитивности). Цвет смеси излучений зависит только от их цветов, а не от их спектрального состава. Отметим, что следствием этого закона является аддитивность цветовых уравнений: если цвета смешиваемых излучений описаны цветовыми уравнениями, то смеси выражаются суммой цветовых уравнений.

 

Именно на этих законах, как на «трех китах», основывается метрология цвета — колориметрия.

Цветовое пространство RGB и цветовой треугольник rgb. Резуль­таты любых измерений должны быть однозначны и сопоставимы. Это одно из требований метрологии. Для его осуществления необходимо, чтобы условия измерений были определены, приняты за норму. Совокупность нормиро­ванных условий измерений цвета составляет колориметрическую систему.

Первая колориметрическая система была принята в 1931 году на Восьмой сессии Международной комиссии по освещению (МКО). Она была положена в основу многих международных рекомендаций по колориметрии и нацио­нальных стандартов [69-73]. В качестве примеров приведем стандарт Герма­нии DIN 5033 [69], наиболее последовательно и полно излагающий основы колориметрии, а также Публикации МКО [71-73] и т. д. Отметим здесь же, что в отечественной и иностранной литературе вместо МКО часто используется аббревиатура Международной комиссии по освещению CIE по первым буквам французского названия МКО Commission Internationale de l'Eclairage.

Резолюцией МКО 1931 года в качестве трех линейно независимых цветов, лежащих в основе этой колориметрической системы, были выбраны следую­щие монохроматические излучения красного, зеленого и синего цветов, обра­зующих так называемую триаду:

· красное излучение на длине волны 700, 0 нм, выделяемое с помощью красного светофильтра из спектра обычной лампы накаливания;

· зеленое излучение на длине волны 546, 1 нм, линия е в спектре ртути;

· синее излучение на длине волны 435, 8 нм, линия g в спектре ртути.

В то время лазер еще не был изобретен, и наиболее приемлемым считалось воспроизведение излучения с помощью газосветных ламп, из которых с по­мощью светофильтров можно было выделить монохроматические излучения определенной длины волны.

Цвета этих излучений были обозначены в соответствии с англоязычными названиями красного, зеленого и синего цветов R, G, В (R — red, G — green, В — blue). Первая колориметрическая система получила название системы RGB.

На той же сессии МКО 1931 года одновременно с системой RGB была принята другая система, основные цвета которой были выбраны более насы­щенными, чем спектральные. Так как таких цветов в природе не существует (об этом см. ниже), то эта система получила название системы XY Z. Эта система была получена искусственно путем пересчета из системы RGB.

Отметим, что система RGB в современной колориметрии используется мало. Однако в дальнейшем рассмотрим ее, так как основы этой системы легко представить, что существенно облегчит понимание принципов колориметрии и преимущества введения цветов системы XYZ.

Выше мы уже отмечали, что цветовая метрика основывается на трех законах Грассмана.

Согласно первому из них любой цвет может быть составлен путем смеше­ния в различной пропорции трех цветов, каждый из которых нельзя получить смешением двух других. Иначе говоря, цвет определяется тремя независимы­ми переменными, составляющими равенство вида

где [R], [G], [В] — единичные количества основных цветов системы измере­ния; R, G, В — доли единичных основных цветов, обеспечивающие цветовое равенство, то есть координаты данного цвета S.

Таким образом, цвет можно характеризовать точкой в пространстве, по­ложение которой задается тремя координатами. Эту точку можно рассматривать, как конец вектора, проведенного из начала координат [66] (рис. 14. 3). Здесь цвет S представлен вектором в вектор­ном пространстве RGB. Цветовые коорди­наты R, G, В представляются проекциями вектора S на координатные оси R, G, В.

Положение самого цветового вектора в цветовом пространстве и его длина не за­висят от выбора основных цветов, а опреде­ляются цветностью и яркостью цвета. На­правление вектора зависит от соотношения цветовых координат и характеризует цвет­ность. Длина вектора зависит от цветовых координат и выражает яркость.

Согласно третьему закону Грассмана, цвет смеси излучений зависит только от их цвета, а не от спектрального состава. То есть, если цвета смешиваемых излучений описаны цветовыми уравнениями, то цвет

Рис. 14. 3. Трехмерная цветовая коор­динатная система RGB смеси выражается суммой цветовых уравнений. Следовательно, если имеются два цвета S1 и S2,

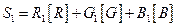
то их сумма описывается уравнением вида

                              (14. 2)

Таким образом, из законов Грассмана вытекает представление о векторе цвета, три составляющие которого имеют общее начало и разные направления в пространстве. Цвет может быть представлен как диагональ параллелепипе­да, построенного на этих составляющих. Совокупность трехмерных векторов цвета составляет цветовое пространство. Каждому цвету соответствует лишь один вектор в цветовом пространстве.

В цветовом пространстве в виде вектора можно представить и ахромати­ческие цвета от черного до белого. Это реализуется, когда координаты цвета равны между собой. В этом случае яркость цвета увеличивается по диагонали куба от черного через оттенки серого до белого.

Диагональ этого куба называется ахроматической осью. По мере уда­ления векторов цвета от ахроматической оси увеличивается насыщенность цвета. Соответственно, чем больше значения цветовых координат, тем больше яркость цвета.

Введем теперь понятие плоскости единичных цветов. Это плоскость, проходящая через отложенные на осях координаты единичных значений вы­бранных основных цветов R, G и В (рис. 14. 4). Сумма координат единичных цветов (или модуль цвета) равна единице.

Каждой точке плоскости единичных цветов соответствует след цветового вектора с модулем, равным единице, пронизывающим плоскость в этой точке. Поэтому цветность любого излучения может быть представлена на плоскости единственной точкой. Так, например, точка белого цвета образуется путем пересечения ахроматической оси с плоскостью в точке N.

Рис. 14. 4. Плоскость единичных цветов и нейтральный цвет N в трехкоординатном цветовом пространстве RGB

 

Плоскость единичных цветов, пересекаясь с координатными плоскостями, образует треугольник, называемый цветовым треугольником или тре­угольником цветности, в вершинах которого находятся точки основных цветов R = 1, G = 1, В = 1.

Теперь может быть сделан очень важный и полезный с практической точки зрения шаг, позволяющий перейти от трехмерного описания цвета к двумер-

ному описанию в прямоугольной системе коор­динат на плоскости.

Оказывается, что для описания цветности не обязательно прибегать к пространственному представлению. Для этого достаточно исполь­зовать плоскость треугольника цветности rgb (рис. 14. 5).

Углы треугольника цветности на рис. 14. 5 представляют собой точки цветности (R), {G) и (В) основных цветов R, G и В, а точка 5 об­разует точку цветности цвета S с координатами цветности г, g и Ь.

В колориметрии принято координаты цве­та обозначать большими буквами, например,

 

Рис. 14. 5. Треугольник цветно­сти rgb или единичная плос­кость трехкоординатного цвето­вого пространства RGB. Кривые сложения цветов системы RGB

 

R, G, В, а координаты цветности, соответственно, маленькими г, g, Ь. Термин «цветность» предполагает корреляцию с чувственно воспринимаемой вели­чиной, раньше называвшейся нами ощущением цветности (она объединяла цветовой тон и насыщенность).

Не трудно понять, что координаты цветности г, g, b связаны с координа­тами цвета R, G, В следующими простыми соотношениями:

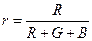
                                            (14. 3)

Отсюда следует, что

                                              (14. 4)

Удобство треугольника цветности состоит в том, что однозначное положе­ние точки любой цветности может быть задано только двумя координатами, например, г и g, а третью b можно найти по двум другим, так как сумма координат цветности равна единице.

Таким образом, цвет графически может быть выражен в виде век­тора в трехмерном пространстве координат цвета RGB или в виде точки, находящейся внутри треугольника цветности в двумерном пространстве координат цветности rg.

Для дальнейшего понимания вопросов метрологии цвета нам необходимо ввести такое важное понятие, как кривые или функции сложения цве­тов.

Используем для измерения цвета прибор, называемый визуальным коло­риметром. Измерение цвета этим прибором основано на том, что с помощью

трех основных цветов колориметрической системы синтезируется цвет, тождествен­ный измеряемому цвету. Схема такого ви­зуального измерения цвета [67] приведена на рис. 14. 6.

Две грани призмы 2, наблюдаемые че­рез диафрагму 1, образуют фотометриче­ское поле, позволяющее сравнивать цвет­ности и интенсивности падающих на приз­му световых лучей. На одну половину поля направляется измеряемое излучение S, на другую — основные излучения (стимулы) красного (R), зеленого (G) и синего (В) цве­тов. Их количества можно регулировать, например, с помощью диафрагм или ней­тральных оптических клиньев, как это по­казано на рис. 14. 6.

e

Рис. 14. 6. Схема измерения цвета с помощью визуального колоримет­ра: 1 — диафрагма, через которую происходит наблюдение; 2 — призма для сравнения цветности и интенсив­ности падающих на нее световых лу­чей

 

Наблюдатель видит обе половины поля и изменяет соотношения количеств основных цветов (или стимулов) на той грани, где происходит смешение цветов, так, чтобы визуально уравнять цвета обеих половин поля зрения. Зная ха­рактеристики светорегулирующих устройств (оптических клиньев, показан­ных на рис. 14. 6), при которых достигается визуальное тождество полей, по значениям коэффициентов пропускания находят количества основных цветов красного (R) с длиной волны 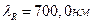, зеленого (G) с длиной волны  и синего (В) с длиной волны , нужных для синтеза цвета, визуально тождественного измеряемому цвету S.

Кроне того, в процессе измерений единицы основных цветов выбираются так, чтобы их энергетические яркости соотносились между собой как  .

Под энергетической яркостью L в точке поверхности и в данном на­правлении понимают отношение энергетической силы света, создавае­мой в данном направлении бесконечно малым элементом поверхно­сти, содержащим указанную точку, к площади ортогональной про­екции этого элемента поверхности на плоскость, перпендикулярную данному направлению. В свою очередь, энергетическая сила света источника в некотором направлении есть частное от деления потока излучения, испускаемого точечным источником (или бесконечно малым элементом протяженной поверхности) в бесконечно малый телесный угол, содержащий указанное направление, к величине этого телесного угла.

Выбор единиц основных цветов с такими отношениями энергетических яркостей определяется из экспериментов, в которых цвет смеси единичных количеств основных цветов уравнивается с цветом равноэнергетическо-го стимула или равноэнергетического излучения. Равноэнергетиче-ский стимул молено представить себе как аддитивную смесь всех мо­нохроматических излучений, составляющих непрерывный спектр видимой области от 380 до 780 нм, в котором каждый стимул или излучение имеет одну и ту же энергетическую яркость.

Результаты подобного эксперимента представляют собой психофизические данные, которые служат основой для построения теории цветового зрения и создания практического метода изме­рения цвета с использованием кривых сложения цветов для, так называемо­го, среднего стандартного наблю­дателя с нормальным цветовым зрением.

В результате проведения вышеопи­санного эксперимента были получены кривые или функции сложения цветов , , , представляющие со­бой функции распределения по спек­тру цветовых координат монохромати­ческих излучений мощностью в 1 Вт в колориметрической системе RGB [66] (рис. 14. 7).

Отметим, что приведенные на рис. 14. 7 кривые (функции) сложения относятся к реальным цветам, явля­ются гладкими и непрерывными. Они имеют положительные и отрицатель ные участки, границы между которыми соответствуют основным цветам: R при 700 нм, G при 546, 1 нм и В при 435, 8 нм.

Длина волны λ, нм

 

Рис. 14. 7. Функции или кривые сложения цветов в колориметрической системе RGB

 

Диаграмма цветности rgb. Локус реальных цветов. Перейдем те­перь к выражению границ реально существующих и наблюдаемых в природе цветов в терминах треугольника цветности и кривых сложения цветов. Так

как более насыщенных цветов, чем спектральные, в природе не существует, то выражающие их точки цветности будут определять границу между реально существующими цветами и нереальными цветами.

Выберем в треугольнике rgb одну из вершин, например 6, за начало координат, отложив значения г = 1 и g = 1 по горизонтали и вертикали, соответственно [70] (рис. 14. 8). Точка Б, имеющая координаты г = 0, 333 и g = = 0, 333, соответствует белому цвету.

 

Рис. 14. 8. Проецирование треугольника цветности на плоскость rg

 

Обозначим на треугольнике rgb значения координат цветности, соответ­ствующих спектральным излучениям от 380 до 700 нм. Для этого воспользуем­ся кривыми сложения цветов, приведенными выше. По их данным определим

положение точек, соответствующих координатам цветности монохромати­ческих излучений. Соединив эти точки между собой, получим линию спек­тральных цветов. Эта кривая полу­чается разомкнутой (рис. 14. 9).

Ее граничные точки соответству­ют максимально насыщенному красно­му ( ) и фиолетовому ( 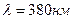) цветам. Замкнув концы гра­ничных точек прямой пунктирной ли­нией, получим геометрическое место точек максимально насыщенных пур­пурных цветов. Так как пурпурные цвета представляют собой смесь крас­ных и фиолетовых излучений и их в ре­альном спектре нет, то на пунктирной

 

Рис. 14. 9. Линия спектральных цветов (или локус реальных цветов) в колоримет­рической системе RGB

линии рис. 14. 9 нереальных пурпурных цветов нет значений длин волн.

 

Эта линия спектральных цветов, представляющая собой геометрическое место точек цветности монохроматических излучений и замкнутая прямой линией пурпурных цветов, называется локусом (от латинского слова locus -место).

Внутри локуса находятся все реальные цвета, т. е. цвета любых физи­чески осуществимых излучений. Вне локуса лежат нереальные (вообра­жаемые) цвета, более насыщенные, чем спектральные, выраженные в данной колориметрической системе.

Нереальные цвета, согласно ГОСТ 13088-67, это цвета, которые харак­теризуют «цветовые векторы, задаваемые в виде линейных комби­наций векторов реальных цветов, такие, однако, которым не соот­ветствуют никакие реальные излучения».

Независимо от выбранной колориметрической системы общими свойства­ми любого локуса являются следующие:

· точка белого цвета Б всегда имеет координаты цветности г = 0, 333 и g = = 0, 333;

· насыщенность цветов возрастает от точки белого цвета к локусу;

· на прямой, соединяющей точку белого цвета с любой точкой локуса, лежат цвета одинакового цветового тона, но разной насыщенности.

Как видно из рис. 14. 9, цветность большой части излучений характеризу­ется отрицательной координатой (г < 0), а у пурпурных цветов координата g также отрицательна (g < 0). Это неудобно, так как затрудняет расчеты цветов по их спектральному составу.

Эти недостатки послужили причиной создания другой, уже упоминавшей­ся нами ранее колориметрической системы Χ Υ Ζ, которая получила широкое распространение и стала основной, стандартной международной колоримет­рической системой, используемой в большинстве цветовых измерений.

Колориметрическая система Χ Υ Ζ. Как уже отмечалось выше, ко­лориметрическая система Χ Υ Ζ свободна от недостатков системы реальных цветов RGB. Триаду Χ Υ Ζ составляют нереальные (воображаемые) цвета, более насыщенные, чем спектральные.

Триада основных линейно независимых цветов в системе Χ Υ Ζ, в со­ответствии с третьим закон Грассмана, пересчитывается путем линейного преобразования из триады RGB следующим образом:

(14. 5)

 

Из вышеприведенных соотношений следует, что:

· цвет X близок по тону к красному (R), но насыщеннее его, так как в соотношении есть член (—0, 0912G);

· цвет Υ много насыщеннее, чем зеленый (G), так как в соотношении имеются две отрицательные координаты (—0Д588Я) и (-0, 0025В);

· цвет Ζ слегка голубее, чем синий (В) и более насыщен (—0, 0829Я). Кроме того, воображаемые цвета X и У не обладают яркостью, котораятеперь может быть получена только из координаты Ζ, что существенно упро­щает расчеты.

В свою очередь, координаты некоторого цвета в системе Χ Υ Ζ равны сумме координат того же цвета в старой системе RGB, при этом каждая из них получена линейным преобразованием при умножении на координаты основных цветов в системе RGB, определенных в системе XYZ:

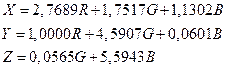                                    (14. 6)

В отличие от системы RGB, кривые (функции) сложения цветов в системе Χ Υ Ζ имеют только положительные значения (сравните с рис. 14. 7) в диапа­зоне всего видимого спектра длин волн от 380 до 780 нм (рис. 14. 10).

Ординаты кривых сложения представляют собой координаты цвета моно­хроматических излучений постоянной мощности в системе Χ Υ Ζ. Они соот­ветствуют угловому размеру поля зрения 2° и определяют так называемого

стандартного колориметрическо­го наблюдателя МКО 1931 г.

Функция у (λ ) совпадает с функ­цией относительной спектральной све­товой эффективности  или кри­вой видности стандартного фото­метрического наблюдения МКО 1931 г. Эта кривая называется еще спектральной кривой видности глаза стандартного наблюдателя с нормальным зрением, то есть яв­ляется некой усредненной кривой спек­тральной чувствительности глаза че­ловека.

Отметим тут же, что в 1964 го­ду МКО приняла рекомендации, опре­деляющие так называемого допол­нительного стандартного колори­метрического наблюдателя с углом

 

Рис. 14. 10. Кривые сложения цветов в ко­лориметрической системе XYZ

зрения, большим 2°, а именно с углом зрения 10°.

 

Были разработаны кривые сложения цветов колориметрической системы X10Y10Z10 и, соответственно, цветовые графики x10, y10 МКО 1964 г. Эти данные были получены на основе результатов многочисленных экспериментов В. Стайлса, Д. Берчема, а также Н. И. Сперанской. В настоящее время эта система находит широкое примене­ние в практике современной колориметрии.

Кривые сложения цветов колориметрической системы XYZ, приведенные на рис. 14. 10, получены в результате тщательных исследований с применением совершенной измерительной техники при строгом соблюдении требований, предъявляемых колориметрией. Они включены в виде подробных таблиц в международные рекомендации [71, 72] и национальные колориметрические стандарты (см., например, DIN 5033 [69]), справочники [68] и т. д.

Цветовой треугольник в системе Χ Υ Ζ представляет собой прямоугольный треугольник. Цветности спектральных излучений располагаются на линии локуса, начало и конец которой замыкаются прямой линией пурпурных цветов (рис. 14. 11). Участок длин волн λ = 580-680 нм практически прямолинеен. Все реальные цветности располагаются внутри этой замкнутой линии. На графике рис. 14. 11 приведена также так называемая линия черного тела и лежащие

 

 

Рис. 14. 11. Локус или цветовой график χ и у в цветовом пространстве МКО 1931 г. Χ Υ Ζ на ней точки, характеризующие цветность и коррелированную цветовую тем­пературу стандартных колориметрических источников излучения типа А, В, С и D65 (см. ниже).

 

Приведем также весьма интересный и полезный рисунок из книги Д. Джадда и Г. Вышецки [66] (рис. 14. 12), иллюстрирующий процесс построения линии локуса в цветовом пространстве МКО 1931 г. Χ Υ Ζ.

Рис 14 12 Трехкоординатное цветовое пространство, построенное на основных цветах МКО 1931 г. Χ, Υ, Ζ

 

 

На рис. 14. 12 приведен график цветности х, у и линия пурпурных цветов. Помимо этого изображена линия, являющаяся геометрическим местом концов векторов, соответствующих спектральным цветам одинаковой энергетической яркости . Точки пересечения векторов  с единичной плоскостью при изменении длины волны λ от значения 400 нм до 700 нм образуют линию чи­стых спектральных цветов на графике цветности. Точки цветности, рас­положенные на прямой линии, соединяющей точки цветности S( 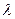 = 400 нм) и S(  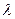= 700 нм), лежат на так называемой линии пурпурных цветов.

Совокупность чистых спектральных цветов S( 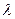) и различных аддитивных смесей S(  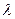= 400 нм) и S(  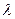= 700 нм) образуют в трехкоординатном цветовом пространстве конус, внутри которого находятся цвета S любых аддитивных смесей спектральных монохроматических цветов. Поверхность этого конуса представляет собой границу всех реально существующих цветов. Цвета, вы­ходящие за пределы конуса, или иначе за пределы цветового охвата системы, называются нереальными цветами, физически не существующими в природе. Отсюда понятно, почему основные цвета системы Χ, Υ, Ζ являются харак­терным примером нереальных цветов.

В отличие от реальной колориметрической системы RGB, координаты цвета в которой могут принимать отрицательные значения, координаты Χ, Υ, Ζ любого реального цвета в системе Χ Υ Ζ никогда не принимают отрицатель­ных значений, так как весь конус расположен в положительном квадранте цветового пространства.

Цвет Е, пересекающий график цветности в точке Ε с координатами x = у = z = 0, 333, представляет собой цвет так называемого равноэнергети-ческого источника излучения.

координаты цветности х, у, zζ связаны с координатами цвета Χ, Υ, Ζ очевидными соотношениями:

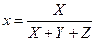
                                                              (14. 7)

И так как χ + у + z = Ι, τ ο обычно при расчетах цветности в системе Χ Υ Ζ ограничиваются только значениями координат x и у.

Координаты цвета Χ, Υ, Ζ могут быть выражены через координаты цветности х, у, z и модуль цвета, обозначаемый тп, и численно равный сумме координат цвета:

                                         (14. 8)

Так как, согласно третьему закону Грассмана (закон аддитивности), цвет смеси цветов выражается через сумму координат цвета смешиваемых цветов (см. формулу 14. 2), то выражения для координат цветности χ и у смеси двух цветов х1, y1 и Х2, у2 будут иметь вид:

                                      (14. 9)

Из уравнений (14. 9) следует, что цветность смеси двух цветов будет изоб­ражаться на цветовом графике х, у (рис. 14. 11) точкой, лежащей на прямой линии, соединяющей цветности смешиваемых цветов. Соответственно, рас­стояния от точек цветности смеси цветов до точек цветности смешиваемых цветов будут обратно пропорциональны модулям этих цветов.

Использование третьего закона Грассмана об аддитивности цветов и вы­текающих из него закономерностей позволяет проводить расчет координат цвета для несамосветящихся образцов отражающих и прозрачных материалов по их измеренным, спектральным коэффициентам отражения и пропускания. Расчет в системе МКО 1931 г. проводится по следующим формулам (пример для отражающих образцов):

                                             (14. 10)

где  — функция относительного спектрального распределения энергии источника излучения, используемого при измерениях; ρ (λ ) — измеренные зна­чения спектральных коэффициентов отражения исследуемого образца; а; (λ ), ,  — ординаты кривых сложения цветов в системе Χ Υ Ζ МКО 1931 г.

При измерении прозрачных образцов в формулах (14. 10) вместо значений спектральных коэффициентов отражения исследуемого образца 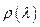 надо ис­пользовать измеренные значения спектральных коэффициентов пропускания прозрачных образцов .

Значения ординат кривых сложения цветов в системе Χ Υ Ζ МКО 1931 г. , ,  в интервале длин волн 380-780 нм с шагом 10 и (или) 5 нм табулированы (см. ГОСТ 13088-67) и приведены в литературе [68, 69] и пуб­ликации МКО [71]. Значения функций 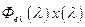, ,  для различных типов источников излучения также табулированы (см. ГОСТ 7721-89. Источники света для измерений цвета. Типы. Технические требования. Маркировка. ) и приводятся в литературе [68] и публикациях МКО [71, 72].

Расчет координат цвета по формулам (14. 10) играет весьма важную роль при проведении измерений координат цвета с помощью спектроколориметри-ческих приборов.

Равноконтрастные колориметрические системы. Колориметриче­ские системы RGB и Χ Υ Ζ МКО 1931 г. дают достаточно полное представ­ление о свойствах цветов, когда используются цветовые графики координат цветности rg или χ у. Однако по этим графикам нельзя получить информацию о степени зрительного восприятия различия цветов, особенно если они кон­трастируют по цветовому тону. Была поставлена задача определения степени различимости цветов на цветовом графике rg или ху. Результатом этих ис­следований явилась разработка новых, так называемых равноконтрастных колориметрических систем.

В 1960 году МКО в качестве стандартного равноконтрастного цветово­го графика был рекомендован цветовой график и, ν, разработанный Мак-Адамом [66] на основе равноконтрастной колориметрической системы UVW. Основные цвета этой системы, так же как и системы Χ Υ Ζ, нереальны. Расчет координат цветности в этой системе может быть произведен по следующим формулам перехода от колориметрической системы Χ Υ Ζ:

                                                (14. 11)

Или

                                                (14. 12)

На рис. 14. 13 приведен равноконтрастный цветовой график и, ν Μ Κ Ο 1960 г., полученный в результате так называемого проекционного преобразо­вания цветового графика х, у МКО 1931 г.

 

Рис. 14. 13. Равноконтрастный цветовой график и, ν (МКО, 1960 г. )

 

В 1964 году на основе равноконтрастного цветового графика МКО 1960 г. по предложению Г. Вышецки была рекомендована новая равноконтрастная колориметрическая система U*V*W* и ее равноконтрастное цветовое про­странство. Координаты этой новой системы связаны с координатами цвета Χ Υ Ζ следующими эмпирическими соотношениями:

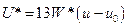
                                               (14. 13)

где u и ν определены в системе МКО 1960 г. по формулам (14. 11) и (14. 12), v0 и v0 — величины u и ν для номинального ахроматического цвета, т. е. координаты белого цвета.

В равноконтрастной системе U*V*W* координаты U* и V* называются показателями хроматичности, а координата W* называется показате­лем светлоты.

Цветовое различие или цветовой контраст  определя­ется по формуле

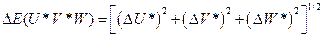                          (14. 14)

Понятие цветовое различие весьма важно при определении цветовых допусков на ту или иную продукцию в лакокрасочной, текстильной, поли­графической и других отраслях промышленности. Отметим, что это понятие справедливо для любой колориметрической системы и может быть определено как корень квадратный из суммы квадратов разницы координат цвета по формуле, аналогичной формуле (14. 14).

В 1976 году МКО рекомендованы для применения две новые модифи­цированные равноконтрастные колориметрические системы и их цветовые пространства L*u*v* и L*a*b*.

Цветовое пространство L*u*v* представляет собой модифицированное цветовое пространство МКО 1964 г. U*V*W*. Координаты цвета L*, u*, ν * определяются следующими соотношениями:

                                     (14. 15)

где u' = 4Х/(Х + 15У + 3Ζ ), ν ' = 9Υ /(Χ + 15У + 3Ζ ), u'0 и v'0 определяются аналогично u' и ν ' с заменой в формулах координат цвета X, У, Ζ на Х0, Υ 0, Z0 — координаты цвета стандартного ахроматического источника излучения, т. е. координаты белого цвета [66, 69, 71].

Координаты цвета X0, Y0, Z0 стандартного ахроматического источника излучения или, иначе, координаты белого цвета обычно задаются из спек­трального распределения энергии излучения одного из стандартных колори­метрических источников излучения, например, А, В, С или D65, отраженной совершенным отражающим рассеивателем. Совершенным отража­ющим рассеивателем называется идеальный однородный рассеива-тель с коэффициентом отражения, равным единице. В этих услови­ях координаты цвета Хо, Yo, Z0 являются координатами цвета выбранного стандартного колориметрического источника излучения, а координата V'o все­гда равна 100. И хотя реальных поверхностей со свойствами совершенного отражающего рассеивателя не существует, с помощью специальных методов можно отградуировать так называемые стандарты белой поверхности в абсолютных единицах. В рекомендации МКО [69], стандарте DIN 5033 [71] и др. приведены значения величин координат цвета совершенного отража­ющего рассеивателя для различных типов колориметрических источников излучения (табл. 14. 1).

 

Таблица 14. 1. Значения величин координат цвета Хо, V'o, Zq совершенного отражающего рассеивателя для различных типов колориметрических источников

излучения [69, 71]

 

 

Колоримет­рические источники излучения	Значения величин координат цвета Хо, Vb, Zo совершенного отражающего рассеивателя в колориметрической системе МКО
	МКО 1931 г. 2°			МКО 1964 г. 10°
	Хо	Уо	я*	Хо	Уо	Zo
А	109, 85	100, 00	35, 58	111, 15	100, 00	35, 20
В	99, 09	100, 00	85, 31	99, 19	100, 00	84, 36
С	98, 07	100, 00	118, 22	97, 28	100, 00	116, 14
D65	95, 05	100, 00	108, 90	94, 81	100, 00	107, 34
D50	96, 42	100, 00	82, 53	96, 72	100, 00	81, 44
D55	95, 67	100, 00	92, 15	95, 79	100, 00	90, 94
D75	94, 96	100, 00	122, 62	94, 41	100, 00	120, 64
Ε	100, 00	100, 00	100, 00	100, 00	100, 00	100, 00

 

В свою очередь, координаты цвета L*, а*, Ь* определяются следующим! соотношениями:

                                                (14. 16)

где X0, Y0, Z0 — координаты цвета стандартного ахроматического источника, т. е. координаты белого цвета [66, 69, 71].

Отметим, что в настоящее время колориметрическая система L*a*b* по­лучает все большее распространение в технике колориметрии.

Стандартные колориметрические источники излучения

Обратимся теперь к вопросу о стандартных колориметрических источни­ках излучения, затронутом в предыдущем па

⇐ Предыдущая48495051525354555657Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: