Дифференциальное уравнение гармонических колебаний и его решение

Г.К.Ильич

МЕДИЦИНСКАЯ И БИОЛОГИЧЕСКАЯ ФИЗИКА

КОЛЕБАНИЯ И ВОЛНЫ

АКУСТИКА

ГЕМОДИНАМИКА

Минск 2000

МИНИСТЕРСТВО ЗДРАВООХРАНЕНИЯ РЕСПУБЛИКИ БЕЛАРУСЬ

МИНСКИЙ ГОСУДАРСТВЕННЫЙ МЕДИЦИНСКИЙ ИНСТИТУТ

КАФЕДРА МЕДИЦИНСКОЙ И БИОЛОГИЧЕСКОЙ ФИЗИКИ

Г.К.Ильич

МЕДИЦИНСКАЯ И БИОЛОГИЧЕСКАЯ ФИЗИКА

КОЛЕБАНИЯ И ВОЛНЫ

АКУСТИКА

ГЕМОДИНАМИКА

Допущено Министерством образования Республики Беларусь в качестве учебного пособия для студентов медицинских высших учебных заведений

Минск 2000

УДК 534.7(075.8)

ББК 22.32 я 73

И 46

 

 

Р е ц е н з е н т ы: кафедра медицинской и биологической физики ГГМУ (заведующий - доцент И.М.Бертель); декан физического факультета БГПУ им. М.Танка профессор В.А.Яковенко; доцент кафедры экологических информационных систем МЭУ им. А.Д.Сахарова В.В.Оболонкин.

Ильич Г.К.

И46 Медицинская и биологическая физика: колебания и волны, акустика, гемодинамика: Учебное пособие для студентов медицинских ВУЗов/ Г.К.Ильич. – Мн.:МГМИ, 2000.- 90 с.

 

ISBN

В соответствии с требованиями программы по медицинской и биологической физике в учебном пособии кратко изложены основы теории колебательных и волновых процессов и представлен учебный материал, направленный на ознакомление студентов-медиков с физическими основами формирования слухового ощущения и акустических измерений, принципами анализа и количественного описания волновых процессов в организме. Рассмотрены физические основы методов ультразвуковой диагностики и акустических воздействий на организм, на которых базируются ультразвуковая терапия и хирургия. Проанализированы физические закономерности, являющиеся основой для количественного описания физиологических процессов в системе кровообращения. Рассмотрены физические методы определения основных гемодинамических параметров.

Предназначено для студентов 1-го курса медицинских ВУЗов

Пособие может быть использовано студентами технических ВУЗов, готовящих специалистов по разработке и обслуживанию медицинской техники, и на биологических факультетах университетов.

УДК 534.7(075.8)

ББК 22.32 я 73

 

Ó Ильич Г.К., 2000

Ó Минский государственный

медицинский институт, 2000

Введение

 

Теория колебательных и волновых процессов, упрощенно рассматриваемая в I-й части пособия, представляет собой важный раздел физики, являясь основой для понимания сущности и количественного описания не только разнообразных физических явлений, но и ряда аспектов жизнедеятельности организма. Знание основ этой теории необходимо медикам для понимания механизмов формирования слухового ощущения, анализа многочисленных периодических процессов в организме и первичной обработки диагностических данных, оценки внешних воздействий на организм акустическими волнами.

Понимание законов акустики, изложению которых посвящена II-я часть, особое значение имеет для грамотного применения и полного использования возможностей широко распространенных в клинической практике методов ультразвукового диагностического исследования. Механизмы взаимодействия акустических волн с веществом и, в частности, с биологическими тканями лежат в основе методик ультразвуковой терапии и хирургии.

Важнейшая функциональная система организма – сердечно-сосудистая. Познание ее деятельности, усвоение современных методов диагностики ее состояния и лечения немыслимо без понимания сущности гемодинамических процессов, которые во многом определяются чисто физическим закономерностями, рассматриваемыми в III-ей части пособия.

Содержание и объем представленного в пособии учебного материала соответствует учебной программе по медицинской и биологической физике для студентов первых курсов медицинских ВУЗов и количеству часов, выделяемых на изучение этого раздела.

 

ЧАСТЬ I

МЕХАНИЧЕСКИЕ КОЛЕБАНИЯ И ВОЛНЫ

Колебаниями называют движения или изменения состояния, повторяющиеся через определенные промежутки времени.

Гармонические колебания

Простейшим видом колебательного движения являются гармонические колебания, когда колеблющаяся величина изменяется со временем по закону синуса или косинуса.

Дифференциальное уравнение гармонических колебаний и его решение

Покажем, что гармоническое колебание возникает под действием упругой силы.

Представим материальную точку массой m, закрепленную на пружине жесткости к и расположенную на абсолютно гладкой горизонтальной поверхности (см. рис. 1). Если растянуть пружину на расстояние х, то со стороны пружины на эту точку действует упругая сила F_y, пропорциональная смещению х по закону Гука:

F_y = - кх.

Знак “минус” указывает на противоположность направлений смещения и действия силы упругости.

Чтобы установить характер движения, т.е. зависимость
х = f(t), запишем для этого случая дифференциальное уравнение, считая что в рассматриваемой системе движение определяется только наличием силы упругости:

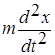= - кх. (1)

Разделим левую и правую части уравнения (1) на m и обозначим отношение положительных величин к и m через w₀² :

 

или . (2)

Решение дифференциального уравнения (2) имеет вид:

х = А₀ sin (w₀ t + j₀) (3)

и показывает, что при наличии в системе лишь силы упругости движение совершается по гармоническому закону. Величина 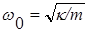, представляет собой циклическую частоту колебаний, А₀ - амплитуду, j₀ - начальную фазу, (w₀ t + j) - фазу колебаний. Период колебаний , а частота
n = 1/ Т.

Зависимость скорости (v) движения материальной точки от времени при гармоническом колебании найдем, взяв производную по времени от формулы (3):

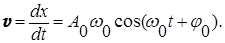(4)

Из сравнения выражений (3) и (4) видно, что смещение и скорость гармонического колебания различаются по фазе на p /2: скорость максимальна при прохождении точкой положения равновесия (смещение равно нулю), наоборот, при максимальном смещении (равном амплитуде) скорость равна нулю.

Выражение для ускорения получается дифференцированием формулы (4):

(5)

Из формулы (3) следует, что смещение и ускорение изменяются в противофазе.

12345678910Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: