Графоаналитический метод кинематического анализа

1.2.2.1 Построение плана скорости

Исходные данные:

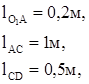
Угловая скорость ведущего звена

 

 

1. Абсолютная скорость точки А₁ на конце ведущего звена 1

 

 

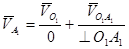
2. Масштабный коэффициент:

 

 

Длинна вектора скорости точки А:

 

 

3. Скорость средней точки первой группы Ассура – точки В определяем через скорости крайних точек этой группы А и О₂.

Скорость точки В относительно точки А:

 

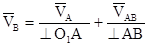
Скорость точки В относительно точки О₂:

 

 

Отрезок  представляет собой вектор скорости точки B, решаем графически.

4. По свойству подобия находим на плане скоростей точку С, которая принадлежит звену 2 и 4, то есть является крайней точкой второй группы Ассура.

Длину вектора 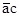 определяем из соотношения:

 

 

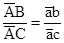
откуда:

 

 

Отрезок  представляет собой вектор скорости точки С.

5. Скорость средней точки второй группы Ассура D₄ определяем через скорости крайних точек этой группы С и О₃.

Скорость точки D₄ относительно точки С:

 

Скорость точки D₄ относительно точки О₃:

 

 

Отрезок  представляет собой вектор скорости точки D₄, решаем графически.

Центры тяжести весомых звеньев определяем по свойству подобия.

6. Пользуясь планом скорости, определяем истинные (абсолютные) значения скоростей точек механизма:

 

 

7. Определяем абсолютные величины угловых скоростей звеньев:

 

 

где lАВ = lАВ∙μ_l =89,38· 0,005 = 0,4469 м

1.2.2.2 Построение плана ускорения

Исходные данные: 1. Кинематическая схема механизма (1 лист)

2. Угловая скорость ведущего звена

3. План скоростей для заданного положения.

1. Абсолютное ускорение точки А на конце ведущего звена:

 

 

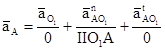
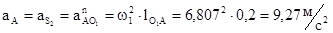
2. Масштабный коэффициент:

 

 

Длина вектора ускорения точки А₁:

 

 

3. Ускорение средней точки первой группы Ассура – точки В₂ определяем через ускорения крайних точек этой группы А и О₂.

Ускорение точки В₂ относительно точки А:

 

 

Ускорение точки В относительно точки О₂:

 

Величина ускорения Кориолиса определяется по модулю формулой:

 

 

Длина вектора, изображающего ускорение Кориолиса на плане ускорений равна:

 

 

Для определения направления ускорения Кориолиса вектор относительной скорости  поворачиваем на 90^о по направлению угловой скорости .

Из конца вектора 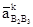 проводим линию действия релятивного ускорения  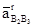параллельную звену АВ.

Решаем графически.

4. По свойству подобия находим на плане ускорения точку С, которая принадлежит звеньям 2 и 4, то есть является крайней точкой второй группы Ассура.

 

 

откуда:

 

5. Ускорение средней точки второй группы Ассура – точки D₄ определяем через ускорения крайних точек этой группы C и О₃, причем точка D₄ принадлежит звену 4 и совпадает с точкой D₅.

Ускорение точки D₄ относительно точки С:

 

 

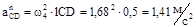
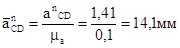
Ускорение точки D₄ относительно точки О₃:

 

 

Решаем графически.

Центры тяжести весомых звеньев определяем по свойству подобия

6. Пользуясь планом ускорений, определяем истинные (абсолютные) значения ускорений точек механизма:

 

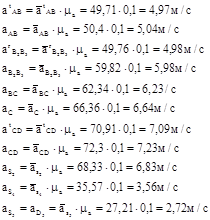
7. Определяем абсолютные величины угловых ускорений звеньев:

 

 

На этом кинематическое исследование кривошипно-ползунного механизма завершено.

 

Силовой анализ плоско-рычажного механизма

 

Определение внешних сил

 

К звену 5 приложена сила полезного сопротивления F_ПС, направление которой указано на схеме.

Величина F_ПС = 1200 Н.

Масса звеньев:

 

 

где q = 10 – вес 1 метра длины звена, кг/м

l_i – максимальная длина звена, м.

Определяем массы звеньев:

 

 

Собственные моменты инерции звеньев относительно оси, проходящей через центр тяжести:

 

 

где - масса звена, кг.

 – длинна звена, м.

Определяем моменты инерции:

 

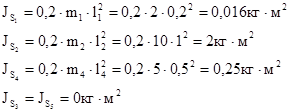
Определяем силы веса по формуле:

 

 

(Принимаем g=10 м/с² – ускорение свободного падения)

 

 

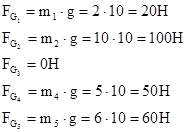
Определяем силы инерции по формуле:

 

 

 

Определяем моменты пар сил инерции по формуле:

 

 

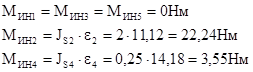
Определяем плечи переноса сил по формуле:

 

 

Направление внешних сил проставлено на кинематической схеме механизма (лист №1 графической части курсового проекта)

 

123456

Поделиться:

Воспользуйтесь поиском по сайту: