 |
Момент сопротивления движению
|
|
|
|
Приведенный к валу кривошипа момент сопротивления движению определяем по формуле:
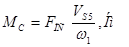
где: 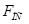 = 1200 Н – сила полезного сопротивления, действует только на рабочем ходу. На холостом ходу
= 1200 Н – сила полезного сопротивления, действует только на рабочем ходу. На холостом ходу 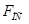 = 0.
= 0.
w1 = 6,81м/с – угловая скорость ведущего звена (кривошипа).
VS5 –скорость выходного звена (ползуна), определенная для 12 положений в первой части курсового проекта.
Значения  для 12 положений механизма сводим в таблицу 5.1.
для 12 положений механизма сводим в таблицу 5.1.
Таблица 5.1.
| № | w 1 1/с | VS 5 м/с |  Н Н
| 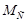 Нм Нм
| 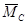 мм мм
|
| 0 | 6,81 | 0,000 | 0 | 0,00 | 0,0 |
| 1 | 6,81 | 1,022 | 1200 | 180,13 | 72,1 |
| 2 | 6,81 | 0,985 | 1200 | 173,67 | 69,5 |
| 3 | 6,81 | 0,876 | 1200 | 154,35 | 61,7 |
| 4 | 6,81 | 0,917 | 1200 | 161,71 | 64,7 |
| 5 | 6,81 | 1,111 | 1200 | 195,81 | 78,3 |
| 6 | 6,81 | 1,332 | 1200 | 234,79 | 93,9 |
| 7 | 6,81 | 1,344 | 1200 | 236,85 | 94,7 |
| 8 | 6,81 | 0,592 | 1200 | 104,37 | 41,7 |
| 9 | 6,81 | -2,691 | 0 | 0,00 | 0,0 |
| 10 | 6,81 | -4,533 | 0 | 0,00 | 0,0 |
| 11 | 6,81 | -1,202 | 0 | 0,00 | 0,0 |
Приведенный момент инерции рычажного механизма
Приведенный момент инерции определяем по формуле:
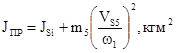
где:  = 0,016кгм2 – момент инерции звена 1;
= 0,016кгм2 – момент инерции звена 1;
m5 = 6 кг – масса пятого звена;
Значения 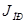 для 12 положений механизма сводим в таблицу 5.2.
для 12 положений механизма сводим в таблицу 5.2.
Таблица 5.2.
| № |  , кгм2 , кгм2
| m 5, кг | w 1 1/с | VS 5, м/с | 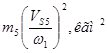
| 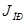 , кгм2 , кгм2
|  , мм , мм
|
| 0 | 0,016 | 6 | 6,81 | 0,000 | 0,0000 | 0,0160 | 1,60 |
| 1 | 0,016 | 6 | 6,81 | 1,022 | 0,1352 | 0,1512 | 15,12 |
| 2 | 0,016 | 6 | 6,81 | 0,985 | 0,1257 | 0,1417 | 14,17 |
| 3 | 0,016 | 6 | 6,81 | 0,876 | 0,0993 | 0,1153 | 11,53 |
| 4 | 0,016 | 6 | 6,81 | 0,917 | 0,1090 | 0,1250 | 12,50 |
| 5 | 0,016 | 6 | 6,81 | 1,111 | 0,1598 | 0,1758 | 17,58 |
| 6 | 0,016 | 6 | 6,81 | 1,332 | 0,2297 | 0,2457 | 24,57 |
| 7 | 0,016 | 6 | 6,81 | 1,344 | 0,2337 | 0,2497 | 24,97 |
| 8 | 0,016 | 6 | 6,81 | 0,592 | 0,0454 | 0,0614 | 6,14 |
| 9 | 0,016 | 6 | 6,81 | -2,691 | 0,9380 | 0,9540 | 95,40 |
| 10 | 0,016 | 6 | 6,81 | -4,533 | 2,6608 | 2,6768 | 267,68 |
| 11 | 0,016 | 6 | 6,81 | -1,202 | 0,1870 | 0,2030 | 20,30 |
Построение графиков (метод Виттенбауэра)
По данным таблицы 5.1. строим диаграмму изменения момента сопротивления в функции от угла поворота кривошипа МС=МС(φ1).
По оси абсцисс откладываем отрезок произвольной длинны, соответствующий полному обороту кривошипа, и делим его на 12 частей, соответствующих 12 положениям механизма.
|
|
|
Масштабный коэффициент угла поворота:
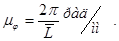
Примем  = 360 мм.
= 360 мм.
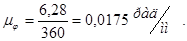
По оси ординат откладываем значение МС для каждого положения механизма в определенном масштабе.
Примем μм = 2,5 Нм/мм.
Графически интегрируя график МС=МС(φ1), строим график работы сил сопротивления в зависимости от угла поворота кривошипа АС=АС(φ1).
Примем Н = 60 мм.
Масштабный коэффициент графика работы:
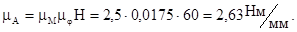
Работа сил сопротивления за один оборот кривошипа равна работе движущих сил. Соединяя прямой линией начало и конец графика работы сил сопротивления, строим график работы движущих сил АД=АД(φ1).
Графически дифференцируя график АД=АД(φ1) на графике МС=МС(φ1) строим график МДМД(φ1) = const (горизонтальная прямая линия).
Величина движущего момента, Нм.

Строим график ΔТ= ΔТ(φ1) в масштабе μТ= μА=2,63Нм/мм.
По данным таблице 5.2. строим график изменения приведенного момента инерции в функции от угла поворота JПР=JПР(φ1). Ось угла поворота направляем вертикально вниз, откладываем на ней отрезок  и делим его на 12 частей
и делим его на 12 частей
Значение JПР откладываем по горизонтальной оси для каждого положения
Примем μ J = 0,01 кгм2/мм.
Имея диаграммы ΔТ= ΔТ(φ1) и JПР=JПР(φ1) строим диаграмму энергомасс ΔТ= ΔТ(JПР), для этого сводим одноименные точки и соединяем их плавной линией.
Определение момента инерции маховика
Для определения момента инерции маховика определяем углы наклона касательных к диаграмме Виттенбауэра Ψmax и Ψmin.

где: wСР = w1 = 6,811/с – угловая скорость кривошипа,
δ=0,04 – коэффициент неравномерности хода.
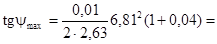 0,0916
0,0916
Ψ max=5,23 o
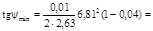 0,0846
0,0846
Ψ min=4,83 o
К Диаграмме Виттенбауэра проводим касательные под найденными углами к горизонтальной оси JПР. Эти касательные пересекают ось ординат в точках а и в. замеряем отрезок ав.
|
|
|
Момент инерции маховика:

По найденному моменту инерции маховика определяем его размеры. Маховик конструктивно выполняем в виде сплошного чугунного диска диаметром – d и шириной – в. Момент инерции сплошного диска относительно его оси равен:
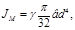
где: g = 7200 кг/м2 – удельная плотность чугуна,
d – диаметр диска,
в - ширина диска.
Примем 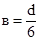 , тогда:
, тогда:

Откуда:
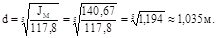
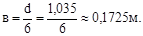
dо = в = 0,17256 м – диаметр отверстия под вал.
Синтез зубчатого механизма
Геометрический синтез зубчатого зацепления
Задачей геометрического синтеза зубчатого зацепления является определение его геометрических размеров и качественных характеристик (коэффициентов перекрытия, относительного скольжения и удельного давления), зависящих от геометрии зацепления.
|
|
|


