 |
Определение внутренних сил
|
|
|
|
Вторая группа Ассура
Структурная группа 2 класса, 2 порядка, 2 модификации.
Изображаем эту группу отдельно. Действие отброшенных звеньев 3 и 0 заменяем силами реакций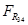 
и 
.
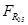В точке О3 на звено 5 действует сила реакции со стороны стойки – 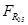, которая перпендикулярна СО3, но неизвестна по модулю и направлению.
В точке С на звено 4 действует сила реакции со стороны звена 2 – 
, тк величина и направление не известно, раскладываем её на тангенсальную и нормальную.
Линия действия тангенсальной составляющей силы реакции перпендикулярна СD. Величину и направление находим из уравнения моментов сил относительно точки D.
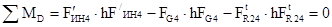
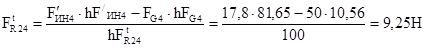
При расчете величина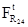 
получилась со знаком (+), т.е. Направление силы выбрано верно.
Векторное уравнение сил, действующих на звенья 4 и 5:
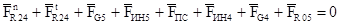
Это векторное уравнение решаем графически, т.е. строим план сил.
Принимаем масштабный коэффициент:
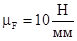
Вектора сил будут равны:
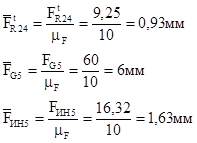
Из плана сил находим:
Первая группа Ассура
Структурная группа 2 класса, 2 порядка, 3 модификации.
Изображаем эту группу отдельно. Действие отброшенных звеньев заменяем силами реакций.
В точке С на звено 2 действует сила реакции со стороны звена 4 – 
, которая равна по модулю и противоположно направлена найденной ранее силе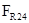 
, т.е. 
.
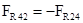В точке О2 на звено 3 действует сила реакции со стороны стойки –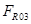 
, которая известна по точке приложения, перпендикулярна звену АВ и неизвестна по модулю и направлению.
В точке А на звено 2 действует сила реакции со стороны звена 1 – 
.
Линия действия этой силы неизвестна, поэтому раскладываем её на нормальную и тангенсальную. Величину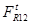 
находим из уравнения моментов сил относительно точки В.
|
|
|
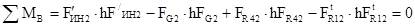
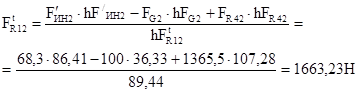
При расчете величина 
получилась со знаком (+), т.е. Направление силы выбрано верно.
Векторное уравнение сил, действующих на звенья 2 и 3:
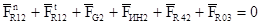
Это векторное уравнение решаем графически, т.е. строим план сил.
Принимаем масштабный коэффициент:
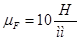
Вектора сил будут равны:
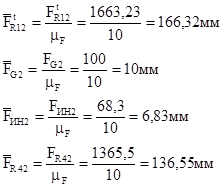
Из плана сил находим:
Определение уравновешивающей силы
Изображаем ведущее звено и прикладываем к нему все действующие силы. Действие отброшенных звеньев заменяем силами реакций.
В точке А на звено 1 действует сила реакции со стороны звена 2 -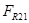 
, которая равна по величине и противоположна по направлению найденной ранее силе реакции 
, т.е. 
.
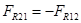В точке О1 на звено 1 действует сила со стороны звена 0 – 
, которую необходимо определить.
Для определения 
составим векторное уравнение сил звена 1:
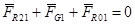
Это векторное уравнение решаем графически, т.е. строим план сил.
Вектора сил будут равны:
Из плана сил находим:
Для уравновешивания звена 1 в точках А и О1 прикладываем уравновешивающие силы –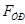 
перпендикулярно звену.
Сумма моментов относительно точки О1:
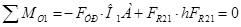
Знак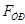 
– положительный, следовательно, направление силы выбрано, верно.
Уравновешивающий момент:
Построенный силовой анализ кривошипно-ползунного механизма изображен на листе №1 графической части курсового проекта.
Определение уравновешивающей силы методом Н.Е. Жуковского
Для определения уравновешивающей силы методом Н.Е. Жуковского строим повернутый в любую сторону план скоростей. Силы, действующие на звенья механизма, переносим в соответствующие точки рычага Жуковского без изменения их направления.
Плечи переноса сил 
и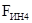 
на рычаге находим из свойства подобия:
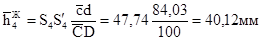
Направление плеча переноса от точки S2 за точку А.
Направление плеча переноса 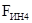от точки S4 к точке С.
|
|
|
Уравнение моментов сил, действующих на рычаг относительно полюса:
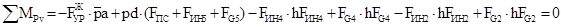
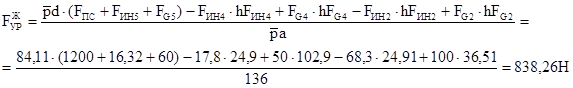
Уравновешивающий момент:
Определение погрешности.
Сравниваем полученные значения уравновешивающего момента, используя формулу:
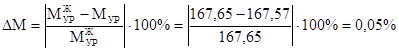
Допустимые значения погрешности менее 3% следовательно, расчеты произведены верно.
На этом силовой анализ кривошипно-ползунного механизма закончен.
Расчет маховика
|
|
|
