 |
3 Моменттер теориясы.
|
|
|
|
Статиканың негізгі ұ ғ ымдары. Статика денеге тү сірілген кү штер жү йесін қ арапайым тү рге келтіретін жә не олардың тепе-тең дік шарттарын тағ айындайтын теориялық механиканың бө лімі.
|
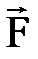
| A |
| M |
| N |
Кү ш алынғ ан масштабта ұ зындығ ы кү штің шамасын анық тайтын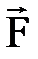 
векторымен бейнеленеді, вектордың басы кү штің тү су нү ктесімен дә л келеді (А нү ктесі), вектордың бағ ыты кү ш бағ ытын анық тайды. Бойымен кү ш векторы бағ ытталғ ан MN тү зуі кү штің ә сер ету сызығ ы деп аталады (1. 1 сурет).
Денеге ә сер ететін ( 
) кү штер жиынтығ ы кү штер жү йесі деп аталады. Егер дененің кү йін ө згертпей оғ ан ә сер ететін ( ) кү штер
1. 1 сурет жү йесін басқ а бір (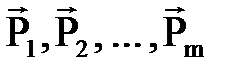 
) кү штер жү йесімен алмастыруғ а болатын болса, мұ ндай екі жү йе пара пар жү йелер деп аталады: ( 
)∾ ( ).
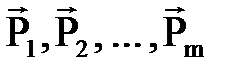Егер дененің кү йін ө згертпей оғ ан ә сер ететін ( ) кү штер жү йесін бір 
кү шпен алмастыруғ а болатын болса, онда бұ л кү ш тең ә серлі кү ш деп аталады: ( )∾ .
Егер дене кү штер жү йесінің ә серінен тепе-тең дікте болса, мұ ндай жү йе тең естірілген немесе нө лге пара пар жү йе деп аталады: ( ) ∾ 0.
|
|
|
1. 1. 2 Статиканың аксиомалары. Статика аксиомаларғ а сү йенеді. Математикалық дә лелсіз қ абылданатын тең деулер мен теоремалар аксиома деп аталады. Олардың шындығ ы адамзаттың, адам қ оғ амының тә жіребесінен туғ ан.
1– аксиома. Екі кү ш ә сер ететін қ атты дене тепе-тең дікте болу ү шін олардың модульдері тең болып, бір тү зудін бойымен қ арама-қ арсы бағ ытталуы қ ажет жә не жеткілікті.
2 – аксиома. Дененің кү йін ө згертпей оғ ан нө лге пара-пар кү штер жү йесін қ осуғ а немесе алып тастауғ а болады.
1 жә не 2 аксиомалардың салдары. Кү шті оның ә сер ету сызығ ының бойымен кез келген басқ а нү ктеге кө шіруге болады, одан кү штің денеге ә сері ө згермейді. Сол себептен кү шті жылжымалы вектор дейді.
| А |
|
|
|
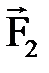
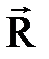
Дене нү ктесіне тү сірілген 
кү штерден параллелограмм тұ рғ ызамыз. Сонда: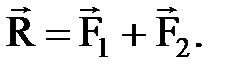 
4 – аксиома. Екі дене бір-біріне шамалары тең, бір тү зудің бойымен қ арама-қ арсы бағ ытталғ ан кү штермен ә сер етеді.
5 – аксиома. Кү штер жү йесі ә сер ететін кез келген деформацияланатын денені тепе-тең діктегі абсолют қ атты дене ретінде қ арастыруғ а болады.
1. 1. 3 Байланыстар жә не олардың реакциялары. Қ озғ алыс еркіндігі басқ а денелермен шектелмеген дене еркін дене деп, ал шектелген дене еркін емес дене деп аталады. Берілген дененің қ озғ алысын шектейтін жә не онымен жанасатын дене байланыс деп аталады. Берілген дене байланысқ а бір кү шпен ә сер етеді. Бұ л кү ш қ ысым кү ші деп аталады. Байланыс та берілген денеге бір кү шпен ә сер етіп, оның қ озғ алысын шектейді. Бұ л кү ш байланыс кү ші (реакция кү ші) немесе байланыс реакциясы деп аталады. Тө ртінші аксиома бойынша қ ысым кү ші мен реакция кү шінің шамалары тең, бір тү зудің бойымен қ арама қ арсы бағ ытталғ ан. Реакция кү штерінің мә ндері денеге ә сер ететін актив кү штерге тә уелді жә не алдын ала белгісіз. Реакция кү штері дененің мү мкін қ озғ алысына қ арсы бағ ытталады. Байланыс дене қ озғ алысын бірнеше бағ ытта шектейтін жағ дайларда реакция кү шінің бағ ыты белгісіз болады. Кейбір байланыстардың реакция кү штерінің бағ ыттарын актив кү штерге тә уелсіз кө рсетуге болады. Осындай байланыстарды қ арастырайық.
|
|
|
Қ озғ алмайтын жылтыр бет (жазық тық ). Егер дене жылтыр беттің ү стінде жатса, мұ ндай байланыстың реакциясы жанасу нү ктесіне тү сіп, жанасушы беттерге ортақ нормаль бойымен бағ ытталады (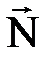 
- нормаль реакция, 1. 2 а) сурет). Егер байланыс денемен ө зінің бір бұ рышымен тү йіссе, реакция денеге перпендикуляр, керісінше жағ дайда реакция байланысқ а перпендикуляр бағ ытталады (1. 2 ә ) сурет).
| ~ |
|
| ~ |
|
| А |
| В |
|
|
|
|
|
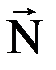
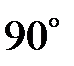
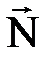
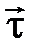
а) ә )
1. 2 сурет 1. 3 сурет
Созылмайтын иілгіш байланыс (жіп, арқ ан, сым арқ ан, шынжыр жә не т. б. ). Реакциясы байланыстың бойымен оның іліну нү ктесіне қ арай бағ ытталады (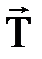 
-керілу кү ші, 1. 3 сурет).
| A |
| B |
|
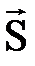
- АВ стерженінің реакциясы, 1. 4 а) суретте стержень сығ ылады, 1. 4 ә ) суретте стержень созылады). |
|
|
| A |
| B |
|
|
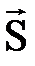
а) 1. 4 сурет ә )
1.
2.
|
| A |
|
| B |
|
|
|
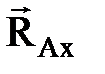
1. 5 сурет
1. 5 суретте жә не кү штері ә сер ететін, А ұ шы цилиндрлік топсамен бекітілген, ал В ұ шы жылтыр бетке сү йенген АВ балкасы келтірілген. Цилиндрлік топсаның белгісіз реакциясының 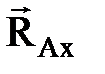жә не екі қ ұ раушысы болады, ал жылтыр беттің реакциясы бетке нормаль бойымен бағ ытталады.
3.
|
|
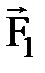
| B |
| A |
|
|
|
|
|
| B |
|
|
|
|
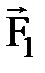
| A |
|
|
|
|
|
|
- цилиндрлік жылжымалы топсаның реакциясы, 1. 6 сурет)
1. 6 сурет
4. Сфералық топса. Мұ ндай топса дененің бір нү ктесін қ озғ алмайтын етеді, бірақ дене сол нү ктені айнала алады. Сол себептен байланыс реакциясы кең істікте кез келген бағ ытта болуы мү мкін. Сфералық топсаның реакциясы 
(1. 7 а) сурет) кең істікте кез келген бағ ытта болуы мү мкін, сондық тан x, y жә не z ө стерімен бағ ытталғ ан ү ш қ ұ раушығ а жіктеледі (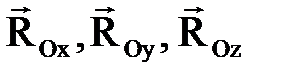 
- сфералық топса реакцияларының қ ұ раушылары, 1. 7 ә ) жә не б) суреттер).
|
|
|
| x |
| y |
| z |
| O |
|
|
|
| x |
| y |
| z |
| O |
|
|
|
|
|
|
а) ә ) б)
1. 7 сурет
Есеп шығ арғ анда байланыстар аксиомасын қ олдану керек.
6 аксиома (байланыстан арылу аксиомасы). Кез келген еркін емес денені еркін дене деп қ арастыруғ а болады. Ол ү шін денеге ә сер ететін байланыстарды алып тастап, олардың ә серін реакция кү штерімен алмастыру керек.
1. 2 Жинақ талатын кү штер жү йесі. Ә сер ету сызық тары бір нү ктеде қ иылысатын кү штер жинақ талатын кү штер деп аталады.
1. 2. 1 Жинақ талатын кү штер жү йесінің тең ә серлі кү ші. Теорема. Жинақ тала- тын кү штер жү йесін осы кү штердің геометриялық қ осындысына тең жә не олар- дың ә сер ету сызық тарының қ иылысу нү ктесіне тү сірілген тең ә серлі кү шпен алмастыруғ а болады (дә лелдеуі дә ріс оқ ығ анда):
. (1. 2. 1)
Жинақ талатын кү штер жү йесінің тең ә серлі кү шін кү штер кө пбұ рышының ә дісімен де анық тауғ а болады. Кө пбұ рышты тұ рғ ызу мысалы дә ріс оқ ығ анда қ арастырылады.
Жинақ талатын кү штер жү йесінің тең ә серлі кү шін кү штің координата ө стеріне проекциялары арқ ылы аналитикалық тү рде анық тауғ а болады. Бұ л жерде векторлардың геометриялық қ осындысының кез келген ө ске проекциясы қ осылғ ыш векторлардың осы ө стерге проекцияларының қ осындысына тең екенін ескереміз. Осығ ан сә йкес, жинақ талатын кү штер жү йесін қ ұ ратын кү штердің декарттық координата ө стеріне проекцияларын біле отырып тең ә серлі кү штің осы ө стерге проекцияларын анық тауғ а болады
. (1. 2. 2)
Сонда тең ә серлі кү штің модулі 
. (1. 2. 3)
Оның бағ ыты бағ ыттаушы косинустармен анық талады
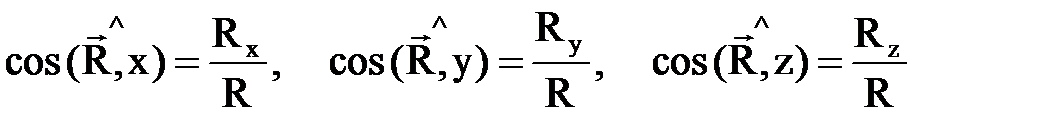. (1. 2. 4)
1. 2. 2 Жинақ талатын кү штер жү йесінің тепе-тең дік шарттары. Теорема. Жинақ талатын кү штер жү йесі тепе-тең дікте болу ү шін оның тең ә серлі кү ші (немесе барлық кү штердің геометриялық қ осындысы) нө лге тең болуы қ ажет жә не жеткілікті (дә лелдеусіз): 
(1. 2. 5)
|
|
|
Геометриялық тұ рғ ыдан бұ л осы кү штерден тұ рғ ызылғ ан кө пбұ рыштың тұ йық болатынын білдіреді, яғ ни соң ғ ы кү штің ұ шы бірінші кү штің басымен дә л келуі керек.
Кең істіктегі жинақ талатын кү штер жү йесінің аналитикалық тепе-тең дік шарттары осы кү штердің координата ө стеріне проекцияларының қ осындысының нө лге тең екендігін білдіреді. Сондық тан, кең істіктегі жинақ талатын кү штер жү йесінің қ ажет жә не жеткілікті тепе-тең дік шарттары былай жазылады:
(1. 2. 6)
Тең деулерге берілген кү штермен қ атар дененің қ озғ алыс еркіндігін шектейтін байланыстардың реакциялары да кіреді.
Сонымен, қ атты денеге ә сер ететін кең істіктегі жинақ талатын кү штер жү йесітепе-тең дікте болу ү шін кү штердің декарттық координата ө стерінің ү шеуінің ә рқ айсысына проекцияларының қ осындысының нө лге тең болуы қ ажет жә не жеткілікті
Сонда, қ атты денеге ә сер ететін жазық тық тағ ы жинақ талатын кү штер жү йесітепе-тең дікте болу ү шін кү штердің декарттық координата ө стерінің екеуіне проекцияларының қ осындысының нө лге тең болуы қ ажет жә не жеткілікті:
(1. 2. 7)
1. 2. 3 Ү ш кү ш туралы теорема. Теорема. Егер параллель емес ү ш кү ш ә сер ететін дене тепе-тең дікте болып, екі кү штің ә сер ету сызық тары қ иылысса, онда кү штердің ү шеуі де бір жазық тық та жатады жә не олардың ә сер ету сызық тары бір нү ктеде қ иылысады (дә лелдеусіз).
3 Моменттер теориясы.
| z |
| 1. 8 сурет |
|
|
|
| A |
| B |
| O |
| x |
| y |
|
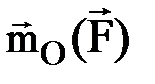
| a |
|
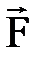
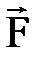кү шінің О нү ктесіне қ атысты моменті деп осы нү к- теге тү скен 
векторды айта- ды. Бұ л вектордың модулі кү ш модулі мен кү штің нү ктеге қ атыс- ты иінінің кө бейтіндісіне тең, ал бағ ыты кү ш пен нү кте арқ ылы ө тетін кү ш жазық тығ ына перпен- дикуляр, оның ұ шынан қ арағ анда кү ш денені сағ ат тіліне қ арсы бағ ытта бұ ратындай болып кө рінеді (1. 8 сурет).
Кү штің О нү ктесіне қ атысты моментінің шамасы немесе модулі:
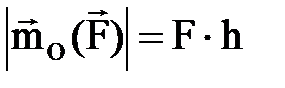. (1. 3. 1)
Кү штің нү ктеге қ атысты иіні деп нү ктеден кү штің ә сер ету сызы- ғ ына дейінгі ең жақ ын ара қ ашық - тық ты(перпендикулярды) айтады.
Кү штің О нү ктесіне қ атыс- ты моментінің векторын кү штің тү су нү ктесінің радиус-векторы мен кү ш векторының векторлық кө бей- тіндісі ретінде жазуғ а болады: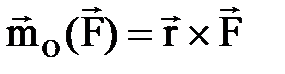 
. (1. 3. 2)
1. 3. 2 Қ ос кү ш жә не оның моменті. Қ ос кү ш деп модульдері тең, бір біріне қ арсы бағ ытталғ ан екі параллель кү штің жү йесін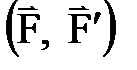 
айтады. Қ ос кү штің ә серінен дене айналмалы қ озғ алыс жасайды, демек, қ ос кү штің моменті болады. Қ ос кү ш жатқ ан 
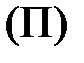жазық тық қ ос кү штің ә сер ету жазық тығ ы деп аталады. Қ ос кү шті қ ұ райтын кү штердің ә сер ету сызық тарының арасындағ ы ең жақ ын ара қ ашық тық (перпендикуляр) қ ос кү штің иіні (d) деп аталады (1. 9 сурет).
екенін ескеріп, кез келген О нү ктеге қ атысты бұ л екі кү штің моменттерінің геометриялық қ осындысын алуғ а болады:
.
Бұ л ө рнек қ ос кү ш моментінің векторы деп аталады, ол О нү ктесіне тә уелсіз:
. (1. 3. 3)
Қ ос кү ш моментінің шамасы оны қ ұ рай-тын кү штердің біреуінің модулі мен қ ос кү ш иінінің кө бейтіндісіне тең:
.
Қ ос кү ш моменті векторының бағ ытық ос кү штің ә сер ету жазық тығ ына перпенди- куляр, ұ шынан қ арағ анда қ ос кү ш денені сағ ат тіліне қ арсы бағ ытта бұ ратындай болып кө рінеді. Оны кез келген нү ктеге тү сіруге болады, себебі ол О нү ктесіне тә уелсіз, демек қ ос кү ш моментінің век- торы жылжымалы вектор екен.
1. 3. 3 Қ ос кү ш туралы теоремалар (дә лелдеусіз). 1-теорема. Бір жазық тық та жатқ ан екі қ ос кү шті моменті осы қ ос кү штер моменттерінің геометриялық қ осындысына тең бір қ ос кү шпен алмастыруғ а болады.
|
|
|
| А |
| В |
| О |
| d |
| П |
| 1. 9 сурет |
2-теорема. Моменттері тең екі қ ос кү ш ө зара пара-пар болады.
1-салдар. Дененің кү йін ө згертпейқ ос кү шті параллель жазық тық қ а кө шіруге болады.
2-салдар. Қ ос кү штің моменті мен айналу бағ ытын сақ тай отырып, оның шамасы мен иінін ө згертуге болады. Одан дененің кү йі ө згермейді.
3-теорема. Қ иылысатын жазық тық тарда жатқ анекі қ ос кү шті осы қ ос кү штер моменттерінің геометриялық қ осындысына тең бір қ ос кү шпен алмастыруғ а болады.
1, 2, 3 теоремалардың салдары. Тү рлі жазық тық тарда жатқ ан қ ос кү штер- дің кез келген санын моменті барлық қ ос кү штер моменттерінің геометриялық қ осындысына тең бір қ ос кү шпен алмастыруғ а болады. Сонымен, денеге ә сер ететін қ ос кү штер жү йесі бір қ ос кү шке пара-пар екен. Тең ә серлі қ ос кү штің 
моменті қ ұ раушы қ ос кү штердің 
моменттерінің геометриялық қ осындысына тең: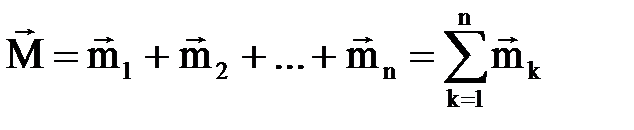 
.
Қ ос кү штер жү йесінің тепе-тең дік шарты. Моменттері қ ос кү штердің ә серіндегі дене тепе-тең дікте болу ү шін барлық қ ос кү штердің моменттерінің геометриялық қ осындысының нө лге тең болуы қ ажет жә не жеткілікті: 
|
|
|
