 |
Жазық қиманың берілген уақытта жылдамдығы нөлге тең нүктесін жылдамдықтардың лездік центрі (ЖЛЦ) деп атайды.
|
|
|
|
Егер жазық қ иманың бұ рыштық жылдамдығ ы нө лге тең болмаса  , жылдамдық тардың лездік центрі болады.
, жылдамдық тардың лездік центрі болады.
Р нү ктесіжылдамдық тардың лездік центрі болсын (2. 9 сурет). Жылдамдық - тардың лездік центрінің жылдамдығ ы нө лге тең болғ андық тан оны полюс етіп алғ ан ың ғ айлы. Сонда В нү ктесі ү шін  , бірақ
, бірақ  , демек,
, демек, 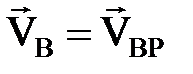 .
.
| А |
| Р |

|
| w |
| В |
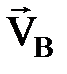
|
| А |
| Р |

|
| w |
| В |
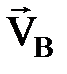
|
| С |
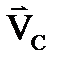
|
2. 9сурет 2. 10 сурет
Сонымен, В нү ктісінің жылдамдығ ының модулі  , (2. 4. 6)
, (2. 4. 6)
векторы ВР-ғ а перпендикуляр w-ның бағ ытымен бағ ытталғ ан ( 2. 9 сурет).
Дә л осылай етсек С нү ктесі ү шін  , яғ ни
, яғ ни 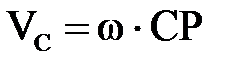 (2. 4. 7)
(2. 4. 7)
бұ л вектор СР-ғ а перпендикуляр w-ның бағ ытымен бағ ытталғ ан ( 2. 9 сурет). Нә тижесінде: 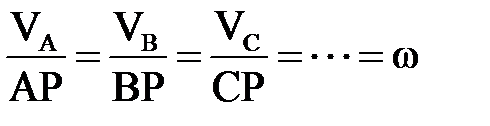 . (2. 4. 8)
. (2. 4. 8)
Сонымен, жазық қ иманың барлық нү ктесінің жылдамдығ ы олардың ЖЛЦ-іне дейінгі ара қ ашық тығ ына пропорционал, ал нү кте жылдамдығ ының векторы осы нү ктені ЖЛЦ-імен қ осатын кесіндіге перпендикуляр бағ ытталғ ан.
ТАҚ ЫРЫБЫ Қ атты дененің жазық -параллель қ озғ алысы (жалғ асы).
Дә ріс конспектісі
2. 4. 5 Жылдамдық тардың лездік центрінің орнын анық таудың дербес жағ дай- лары. ЖЛЦ-інің негізгі қ асиеттерін қ олданып, жазық қ има нү ктелері жылдамдық - тарының ә ртү рлі бағ ыттары ү шін ЖЛЦ-інің орнын анық тауғ а болады.
|
|
|
1. Жазық қ иманың бір нү ктесінің (А нү ктесі) жылдамдығ ының шамасы мен бағ ыты, ал екінші нү ктесінің (В нү ктесі) жылдамдығ ының бағ ыты белгілі (2. 10 сурет). ЖЛЦ. (Р нү ктесі) А жә не В нү ктелерінен олардың жылдамдық тары векторларының бағ ыттарына жү ргізілген перпендикулярлардың қ иылысу нү кте- сінде жатады.  векторының бағ ытымен
векторының бағ ытымен  векторы жә не w бұ рыштық жылдамдық тың бағ ыты анық талады. (2. 4. 8) ө рнегінен жазық қ иманың барлық нү ктесінің жылдамдығ ын жә не қ иманың бұ рыштық жылдамдығ ын табуғ а болады.
векторы жә не w бұ рыштық жылдамдық тың бағ ыты анық талады. (2. 4. 8) ө рнегінен жазық қ иманың барлық нү ктесінің жылдамдығ ын жә не қ иманың бұ рыштық жылдамдығ ын табуғ а болады.
| А |
| Р |

|
| w |
| В |
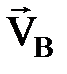
|
| Р |
| А |
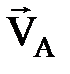
|
| А |

|
| В |
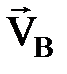
|
| a |
| a |
| Р |

|
| w |
| В |
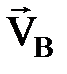
|
а) б) 2. 13 сурет
2. 11 сурет 2. 12 сурет
2. Екі нү ктенің (А жә не В нү ктелері) жылдамдық тарының векторлары парал- лель, шамалары белгілі жә не осы нү ктелерді қ осатын тү зуге перпендикуляр бағ ытталғ ан (2. 11 сурет). ЖЛЦ. (Р нү ктесі) жылдамдық тар векторларының басы мен ұ шы арқ ылы жү ргізілген тү зулердің қ иылысу нү ктесінде жатады. Қ иманың w бұ рыштық жылдамдығ ының бағ ыты нү кте жылдамдық тарының бағ ытымен анық - талады, ал оның шамасын жә не қ иманың басқ а нү ктесінің жылдамдығ ын (2. 4. 8) ө рнегінен табуғ а болады.
3. Екі нү ктенің (А жә не В нү ктелері) жылдамдығ ының векторлары параллель, бірақ осы нү ктелерді қ осатын тү зуге перпендикуляр емес (2. 12 сурет).  жә не
жә не  векторларына перпендикуляр тү зулер қ иылыспайды, демек ЖЛЦ шесіздікте жатыр, яғ ни ЖЛЦ жоқ. Жылдамдық тардың проекциялары туралы теорема бойын- ша
векторларына перпендикуляр тү зулер қ иылыспайды, демек ЖЛЦ шесіздікте жатыр, яғ ни ЖЛЦ жоқ. Жылдамдық тардың проекциялары туралы теорема бойын- ша  . Осыдан
. Осыдан 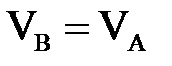 жә не
жә не 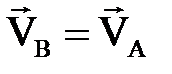 ; басқ а нү ктелер ү шін де осылай болады. Сондық тан (2. 4. 8) ө рнегінен,
; басқ а нү ктелер ү шін де осылай болады. Сондық тан (2. 4. 8) ө рнегінен, 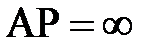 болғ андық тан, бұ рыштық жылдамдық w = 0 болады.
болғ андық тан, бұ рыштық жылдамдық w = 0 болады.
|
|
|
Бұ л жағ дайда дене лездік ілгерілемелі қ озғ алыс жасайды,
4. Дене қ озғ алмайтын бетпен сырғ анамай домалайды (2. 13 сурет). ЖЛЦ (Р нү ктесі) денелердің жанасу нү ктесінде жатады.
Жазық -параллель қ озғ алыстың айналмалы қ озғ алыстан айырмашылығ ы – ЖЛЦ ө зінің жазық тық тағ ы орнын ө згертіп отырады.
2. 4. 6 Жазық -параллель қ озғ алыстағ ы дене нү ктелерінің ү деуі. Жазық қ има- ның кез келген нү ктесінің ү деуін анық тау ү шін (2. 4. 4) ескеріп, (2. 4. 3) ө рнегін дифференциалдайық:  . (2. 4. 9)
. (2. 4. 9)
Соң ғ ы екі қ осылғ ыш А нү ктесі бекітулі болғ ан кездегі В нү ктесінің ү деуін анық тайды, сондық тан олардың қ осындысы А нү ктесінен қ има жазық тығ ына перпендикуляр ө тетін қ озғ алмайтын ө сті айналғ андағ ы В нү ктесінің ү деуін береді : 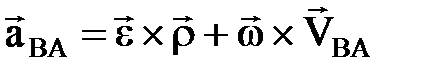 . (2. 4. 10)
. (2. 4. 10)
Біз нү кте ү деуінің бұ л қ ұ раушыларымен қ атты дененің айналмалы қ озғ алы- сында кездескенбіз. Оларды сондағ ы атаулармен қ алдырып, В нү ктесінің А нү ктесін а йналғ андағ ы ү деуінің центрге тартқ ыш жә не айналмалы қ ұ раушылары деп атаймыз. Бұ л ү деулердің модульдеріВ нү ктесінің А нү ктесін айналғ андағ ы ү деуінің центрге тартқ ыш
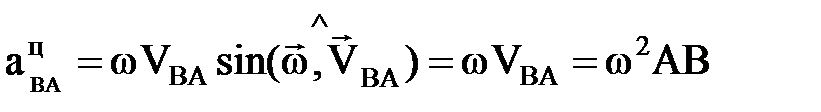 (2. 4. 11)
(2. 4. 11)
жә не айналмалы ү деулері деп аталады:
 (2. 4. 12)
(2. 4. 12)
Айналмалы қ озғ алыстың ережелеріне сә йкес,  векторы В нү ктесінен А нү ктесіне қ арай, ал
векторы В нү ктесінен А нү ктесіне қ арай, ал  векторы
векторы  -ғ а перпендикуляр e бағ ытымен бағ ытталады (2. 14 сурет).
-ғ а перпендикуляр e бағ ытымен бағ ытталады (2. 14 сурет).
|
|
|
| А |
В 
|
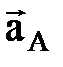
|
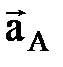
|
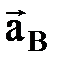
|

|

|

|
| e |
| А |
В 
|
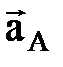
|
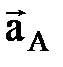
|
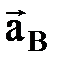
|

|

|

|
| e |
2. 14 сурет
Жоғ арыда айтылғ андарды ескерсек, (2. 4. 9) тең деуін былай жазуғ а болады:
 , (2. 4. 13)
, (2. 4. 13)
бұ л – жазық -параллель қ озғ алыстағ ы дене нү ктелерінің ү деулерін қ осу тура- лы теорема. Сонымен, жазық -параллель қ озғ алыстағ ы дененің кез келген нү кте- сінің ү деуі полюстің (А нү ктесі) ү деуі мен осы нү ктенің (В нү ктесі) полюсті айналғ андағ ы центрге тартқ ыш жә не айналмалы ү деулерінің векторлық қ осындысынан тұ рады екен.
В нү ктесі ү деуінің модулі
3. 1 Динамикағ а кіріспе. Динамика – материялық денелердің қ озғ алысын оларғ а ә сер ететін кү штермен бірге зерттейтін теориялық механиканың бө лімі. Динамикада тек тұ рақ ты кү штер ғ ана емес, сонымен бірге уақ ытқ а (тарту кү штері), координатағ а (гравитациялық тартылыс кү штері, кулондық тартылыс кү штері, серпімділік кү штері) жә не жылдамдық қ а (ортаның кедергі кү штері) тә уелді айнымалы кү штер де қ арастырылады. Айнымалы кү штер тұ рақ ты кү штердің заң дарына бағ ынады, яғ ни оларды қ осуғ а, жіктеуге болады, олардың моменттері жә не т. б. болады.
3. 2 Материялық нү кте динамикасы. Материялық нү кте деп қ озғ алы-сын зерттегенде ө лшемдерін ескермеуге болатын материялық денені айтады.
3. 2. 1 Материялық нү кте динамикасының негізгі заң дары. Ньютонның ү ш заң ы материялық нү кте динамикасының негізгі заң дары болады.
Ньютонның бірінші заң ы. Егер материялық нү ктеге сырттан ешбір кү ш ә сер етпесе немесе ә сер ететін кү штер жү йесі нө лге пара-пар болса, онда нү кте тыныштық кү йде немесе бірқ алыпты жә не тү зу сызық ты қ озғ алыста болады. Ньютонның бірінші заң ы орындалатын санақ жү йелері инерциялық санақ жү йелері деп. аталады.
|
|
|
Ньютонның екінші заң ы (динамиканың негізгі заң ы). Материялық нү ктенің ү деуі оғ ан ә сер етуші кү шке тура пропорционал, бағ ыты кү шпен бағ ыттас. Нү кте массасы пропорционалдық коэффициенті болады.
Бұ л заң ның математикалық ө рнегі: 
 . (3. 2. 1)
. (3. 2. 1)
Егер денеге бірнеше  кү штер ә сер етсебұ л заң былай жазылады:
кү штер ә сер етсебұ л заң былай жазылады:
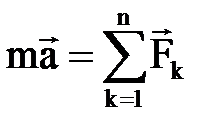 . (3. 2. 2)
. (3. 2. 2)
Ньютонның ү шінші заң ы. Екі материялық нү кте бір-біріне модульдері тең, бір тү зудің бойымен қ арама-қ арсы бағ ытталғ ан кү штермен ә сер етеді.
3. 2. 2 Нү кте динамикасының негізгі мә селелері. Материялық нү ктенің негізгі мә селелері еркін жә не еркін емес нү ктелер ү шін айтылады..
Қ озғ алысы басқ а денелермен шектелмеген нү ктені еркін материялық нү кте дейміз. Осындай нү кте ү шін динамиканың екі негізгі мә селесі қ арастырылады:
Динамиканың бірінші негізгі мә селесі: Нү ктенің массасы мен қ озғ алыс заң ын біле отырып, оғ ан ә сер ететін кү штерді анық тау.
Динамиканың екінші негізгі мә селесі: Нү ктенің массасы мен оғ ан ә сер ететін кү штерді біле отырып, оның қ озғ алыс заң ын анық тау.
Екі мә селе де Ньютонның екінші (3. 2. 2) заң ының кө мегімен шешіледі.
Қ озғ алысы басқ а денелермен шектелген нү кте еркін емес материялық нү кте деп аталады. Мұ ндай нү кте ү шін оғ ан ә сер ететін барлық актив  кү штерге реакция кү штерін қ осу қ ажет. Оларды бір кү шпен
кү штерге реакция кү штерін қ осу қ ажет. Оларды бір кү шпен  белгілейміз. Сонда Ньютонның екінші заң ы былай жазылады:
белгілейміз. Сонда Ньютонның екінші заң ы былай жазылады:
 . (3. 2. 3)
. (3. 2. 3)
(3. 2. 3) ө рнегімен еркін емес нү кте ү шін де динамиканың екі негізгі мә селесі шешіледі:
Динамиканың бірінші негізгі мә селесі: Нү ктенің массасын, қ озғ алыс заң ын жә не оғ ан ә сер ететін актив кү штерді біле отырып, реакция кү штерін анық тау.
Динамиканың екінші негізгі мә селесі: Нү ктенің массасын жә не оғ ан ә сер ететін актив кү штерді біле отырып, оның қ озғ алыс заң ын жә не реакция кү штерін анық тау.
|
|
|
Нү кте динамиканың бірінші негізгі мә селесінің шешуі. Бұ л мә селені шешу ү шін Ньютонның екінші заң ын қ ұ рып, сосын оны координата ө стеріне проекциялау керек.
3. 2. 3 Материялық нү кте қ озғ алысының дифференциалдық тең деулерін интегралдау. Материялық нү ктенің инерциялық санақ жү йесіндегі орнын  радиус-векторымен анық таймыз. Нү ктеге ә сер ететін кү ш жалпы жағ дайда t уақ ытқ а, нү ктенің орнына, яғ ни
радиус-векторымен анық таймыз. Нү ктеге ә сер ететін кү ш жалпы жағ дайда t уақ ытқ а, нү ктенің орнына, яғ ни  радиус-векторғ а жә не нү ктенің
радиус-векторғ а жә не нү ктенің  жылдамды- ғ ына тә уелді бола алады, яғ ни
жылдамды- ғ ына тә уелді бола алады, яғ ни  . Егер нү ктенің ү деуі
. Егер нү ктенің ү деуі 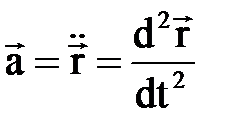 , ал жылдамдығ ы
, ал жылдамдығ ы 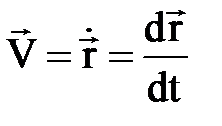 екенін ескерсек, Ньютонның екінші заң ы немесе нү кте динамикасының негізгі тең деуі былай жазылады:
екенін ескерсек, Ньютонның екінші заң ы немесе нү кте динамикасының негізгі тең деуі былай жазылады:
 . (3. 2. 4)
. (3. 2. 4)
(3. 2. 4) – векторлық тү рдегі нү кте қ озғ алысының дифференциалдық тең деуі.
(3. 2. 4) тең деуі декарттық координата жү йесінің ө стеріне проекцияланғ ан ү ш скаляр тең деуге пара-пар:  . (3. 2. 5)
. (3. 2. 5)
Нү кте динамикасының екінші мә селесінің шешуі белгісіз x, y, z функцияла- рына қ атысты екінші дә режелі ү ш дифференциалдық тең деу жү йесінен тұ ратын оның қ озғ алысының дифференциалдық тең деулерін интегралдауғ а тіреледі.
Бұ л тең деулердің жалпы шешімі С1, С2, …, С6 алты интегралдау тұ рақ тыла- рына тә уелді:
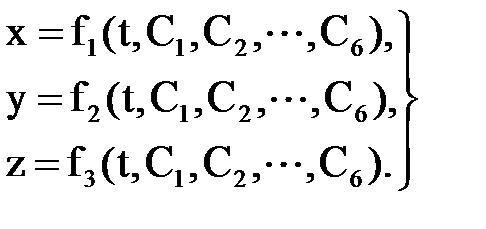 (3. 2. 6)
(3. 2. 6)
Интегралдау тұ рақ тылары ә ртү рлі мә нге ие бола алады, сондық тан бірдей кү ш ә сер ететін нү кте тү рлі қ озғ алыс жасай алады. Сонымен, нү кте қ озғ алысының нақ ты заң ын анық тау ү шін тек кү штің берілуі жеткіліксіз екен. (3. 2. 6) шешуі шығ арылып отырғ ан нақ ты мә селеге сә йкес болу ү шін қ озғ алыстың бастапқ ы шарттарын беру қ ажет, яғ ни нү ктенің
бастапқ ы орны мен бастапқ ы жылдамдығ ын беру қ ажет екен.
Декарттық координата жү йесінде сә йкес проекцияларды беру керек. Бастапқ ы шарттар:
t=0:  . (3. 2. 7)
. (3. 2. 7)
(3. 2. 7) бастапқ ы шарттар (3. 2. 6) шешулері мен олардың бірінші туындыларына қ ойылады. Осылай алынғ ан тең деулерден интегралдау тұ рақ тылары табылады
 (3. 2. 8)
(3. 2. 8)
Табылғ ан тұ рақ тыларды (3. 2. 6) жалпы шешімге қ ойып, берілген бастапқ ы шарттарғ а сә йкес келетін есептің шешуін аламыз.
3. 4 Нү кте динамикасының жалпы теоремалары. Нү кте динамикасының есептерін шығ арғ анда нү кте қ озғ алысының дифференциалдық тең деулерін интег- ралдау қ ажет. Кө п жағ дайда бұ л тең деулерді интегралдау оң ай емес. Сондық тан нү кте динамикасының жалпы теоремаларын пайдаланады. Есеп шығ арғ анда дифференциалдық тең деулерді интегралдамай, аталмыш теоремалардың қ оры- тынды ө рнектерін пайдаланады. Ал дифференциалдық тең деулер теоремаларды дєлелдегенде интегралданады.
3. 4. 1 Нү ктенің қ озғ алыс мө лшері. Кү ш импульсі. Нү кте қ озғ алысының негізгі динамикалық сипаттамаларының бірі – қ озғ алыс мө лшері.
Нү ктенің қ озғ алыс мө лшері деп оның массасы мен жылдамдық векторының кө бейтіндісіне тең ( 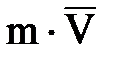 ) векторлық шаманы айтады: Қ озғ алыс мө лшерінің векторы ә рқ ашан нү ктенің жылдамдығ ымен бағ ыттас болады (3. 3 сурет).
) векторлық шаманы айтады: Қ озғ алыс мө лшерінің векторы ә рқ ашан нү ктенің жылдамдығ ымен бағ ыттас болады (3. 3 сурет).
Белгілі уақ ыт аралығ ындағ ы кү штің нү ктеге ә серін кү ш импульсі дейді.
Кү штің элементар импульсі деп кү ш векторының элементар уақ ытқ а кө бейтіндісіне тең векторлық шаманы айтады:
 . (3. 4. 1)
. (3. 4. 1)
Бұ л вектор кү штің ә сер ету сызығ ының бойымен бағ ытталады.
Шекті уақ ыт аралығ ындағ ы кү ш импульсі 0-ден t1-ге дейінгі аралық тағ ы элементар импульстен алынғ ан интегралғ а тең:
 . (3. 4. 2)
. (3. 4. 2)
Кү ш импульсін екі жағ дайда санауғ а болады:
1. Егер кү штің сан шамасы мен бағ ыты тұ рақ ты болса ( 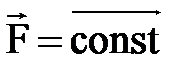 ), онда
), онда  .
.
2. Егер кү ш уақ ытқ а тә уелді функция болса.
Егер кү ш нү ктенің орнына немесе жылдамдығ ына тә уелді болса, кү ш импульсін санау ү шін нү ктенің қ озғ алыс заң ын білу қ ажет.
Есеп шығ арғ анда кү ш импульсін координата ө стеріне проекциялайды, декарттық координата жү йесі ү шін бұ л проекциялар былай жазылады:
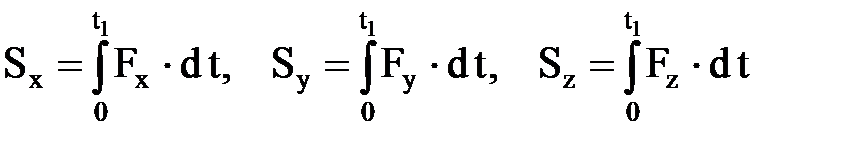 . (3. 4. 3)
. (3. 4. 3)
3. 4. 2 Нү ктенің қ озғ алыс мө лшерінің ө згеруі туралы теорема. Нү кте ү деуінің векторы жылдамдық векторынан уақ ыт бойынша алынғ ан бірінші туындығ а тең  екенін ескерсек, нү кте динамикасының негізгі заң ын (
екенін ескерсек, нү кте динамикасының негізгі заң ын (  ) былай жазуғ а болады:
) былай жазуғ а болады:
 . (3. 4. 4)
. (3. 4. 4)
(3. 4. 4) – нү ктенің қ озғ алыс мө лшерінің ө згеруі туралы теореманың диффе ренциалдық тү рі: нү ктенің қ озғ алыс мө лшерінен уақ ыт бойынша алынғ ан туынды нү ктеге ә сер ететін барлық кү штердің геометриялық қ осындысына тең.
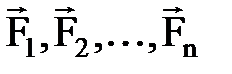 кү штері ә сер ететін М нү ктенің
кү штері ә сер ететін М нү ктенің 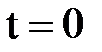 ден
ден 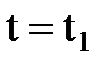 –ге дейінгі шекті уақ ыт аралығ ында М0-ден М1-ге орын ауыстыруын қ арастырайық. Оның жылдам- дығ ы
–ге дейінгі шекті уақ ыт аралығ ында М0-ден М1-ге орын ауыстыруын қ арастырайық. Оның жылдам- дығ ы  -ден
-ден  -ге дейін ө згерсін. (3. 4. 4) тең деуінің екі жағ ын да dt-ғ а кө бейтіп, екі жағ ынан да интеграл алайық:
-ге дейін ө згерсін. (3. 4. 4) тең деуінің екі жағ ын да dt-ғ а кө бейтіп, екі жағ ынан да интеграл алайық:
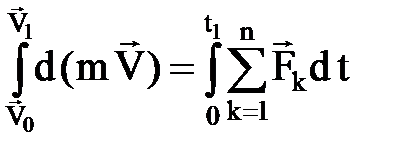 немесе
немесе  .
.
Егер (3. 4. 2) ө рнегін ескеретін болсақ:
 . (3. 4. 5)
. (3. 4. 5)
(3. 4. 5) – нү ктенің қ озғ алыс мө лшерінің ө згеруі туралы теореманың интег- ралдық (шекті) тү рі: шекті уақ ыт аралығ ындағ ы нү ктенің қ озғ алыс мө лшерінің ө згеруі осы уақ ыт аралығ ында нү ктеге ә сер ететін барлық кү ш импульстерінің геометриялық қ осындысына тең.
Есеп шығ арғ анда (3. 4. 5) теореманы координата ө стеріне проекциялау керек. Декарттық координата жү йесінің ө стеріне проекцияласақ:
 (3. 4. 6)
(3. 4. 6)
3. 4. 3 Нү ктенің қ озғ алыс мө лшерінің моменті жә не оның ө згеруі туралы теорема. Кейбір есептерде динамикалық сипаттамалар ретінде нү ктенің центрге немесе ө ске қ атысты қ озғ алыс мө лшерінің моменті қ арастырылады.
Нү ктенің О центріне қ атысты қ озғ алыс мө лшерінің моменті деп
 (3. 4. 7)
(3. 4. 7)
ө рнекпен анық талатын 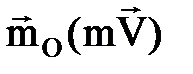 векторлық шаманы айтады, мұ ндағ ы
векторлық шаманы айтады, мұ ндағ ы  - нү кте- нің О центріне қ атыстырадиус-векторы. Бұ л вектор
- нү кте- нің О центріне қ атыстырадиус-векторы. Бұ л вектор  векторы мен О центрі арқ ылы ө тетін жазық тық қ а перпендикуляр, ұ шынан қ арағ анда
векторы мен О центрі арқ ылы ө тетін жазық тық қ а перпендикуляр, ұ шынан қ арағ анда  векторынан
векторынан  векторына қ арай ең жақ ын бұ рылу сағ ат тіліне қ арсы болып кө рінетіндей бағ ыт- талғ ан. Оның сан шамасы
векторына қ арай ең жақ ын бұ рылу сағ ат тіліне қ арсы болып кө рінетіндей бағ ыт- талғ ан. Оның сан шамасы  , бұ л жердегі h – О центрінен М нү ктеден траекторияғ а жү ргізілен жанама арасындағ ы ең жақ ын ара қ ашық тық (перпендикуляр).
, бұ л жердегі h – О центрінен М нү ктеден траекторияғ а жү ргізілен жанама арасындағ ы ең жақ ын ара қ ашық тық (перпендикуляр).
(3. 4. 7) векторының ө ске проекциясы нү ктенің ө ске қ атыстық озғ алыс мө лшерінің моментін анық тайды. Декарттық координата жү йесінің ө стері ү шін, кү штердің моменттері сияқ ты, нү ктенің x, y жә не z ө стеріне қ атысты қ озғ алыс мө лшерінің моменттерінің аналитикалық ө рнектерін жазуғ а болады:
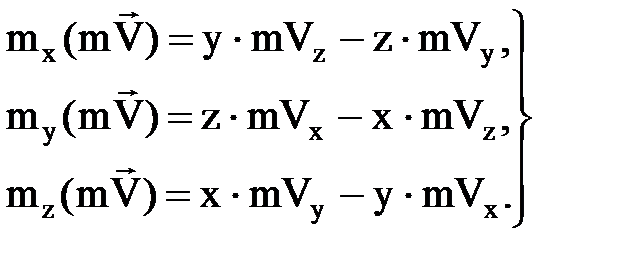 . (3. 4. 8)
. (3. 4. 8)
Бұ л тең деулердегі x, y, z – нү кте координаталары, Vx, Vy, Vz – нү кте жылдам- дығ ының координата ө стеріне проекциялары.
Нү ктенің қ озғ алыс мө лшері моментінің ө згеруі туралы теорема уақ ыт ө ткен сайынғ ы 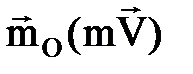 векторының ө згеруін анық тайды. Оны дә ріс оқ ығ анда дә лелдейміз.
векторының ө згеруін анық тайды. Оны дә ріс оқ ығ анда дә лелдейміз.
 . (3. 4. 9)
. (3. 4. 9)
Бұ л тең деу нү ктенің центрге қ атысты қ озғ алыс мө лшері моментінің ө згеруі туралытеореманы білдіреді: нү ктенің кез келген О центріне қ атысты қ озғ алыс мө лшері моментінен уақ ыт бойынша алынғ ан туынды нү ктеге ә сер ететін кү штің осы центрге қ атысты моментіне тең.
(3. 4. 9) векторлық тең деу ү ш скалярлық тең деуге пара-пар.
 . (3. 4. 10)
. (3. 4. 10)
(3. 4. 10) тең деулері нү ктенің x, y, z координата ө стеріне қ атысты қ озғ а- лыс мө лшері моменттерінің ө згеруі туралы теорема болады: нү ктенің кез келген ө ске қ атысты қ озғ алыс мө лшері моментінен уақ ыт бойынша алынғ ан туынды нү ктеге ә сер ететін кү штің осы ө ске қ атысты моментіне тең.
Қ озғ алыс мө лшерінің моменті ү шін екі сақ талу заң ы орындалады:
1. Егер ә сер ететін кү штің бір центрге қ атысты моменті нө лге тең болса, онда нү ктенің осы центрге қ атысты қ озғ алыс мө лшері моментінің сан шамасы мен бағ ыты тұ рақ ты болады.
Егер ә сер ететін кү штің бір ө ске қ атысты моменті нө лге тең болса, онда нү ктенің осы ө ске қ атысты қ озғ алыс мө лшерінің моменті тұ рақ ты болады. Бұ л тұ жырымды (3. 4. 10) ө рнегі береді
3. 4. 4 Кү ш жұ мысы. Қ уат. Нү кте орын ауыстырғ андағ ы кү ш ә серін сипаттау ү шін жұ мыс ұ ғ ымын қ олданады. М нү ктесіне ә сер ететін  кү шінің (3. 3 сурет) элементар жұ мысы деп мына скаляр шаманы айтады
кү шінің (3. 3 сурет) элементар жұ мысы деп мына скаляр шаманы айтады
 , (3. 4. 11)
, (3. 4. 11)
мұ ндағ ы  -
-  кү шінің Мt жанама ө ске проекциясы (немесе
кү шінің Мt жанама ө ске проекциясы (немесе  кү шінің М нү ктесінің
кү шінің М нү ктесінің  жылдамдығ ы бағ ытына проекциясы); ds – М нү ктесінің элементар орын ауыстыру модулі.
жылдамдығ ы бағ ытына проекциясы); ds – М нү ктесінің элементар орын ауыстыру модулі.
 (a -
(a -  жә не Мt арасындағ ы бұ рыш) болғ андық тан, (3. 4. 11) ө рнегінен кү штің элементар жұ мысының тағ ы бір ө рнегін аламыз:
жә не Мt арасындағ ы бұ рыш) болғ андық тан, (3. 4. 11) ө рнегінен кү штің элементар жұ мысының тағ ы бір ө рнегін аламыз:
 . (3. 4. 12)
. (3. 4. 12)
(3. 4. 12) ө рнегінен мынаны тұ жырымдаймыз:
1. Егер a бұ рышы сү йір болса (0< a< 900), жұ мыс оң таң балы болады. Ал a = 0 болғ анда элементар жұ мыс  .
.
2. Егер a бұ рышы доғ ал болса (900 < a < 1800), жұ мыс теріс таң балы болады. Ал a = 1800 болғ анда элементар жұ мыс  .
.
3. Егер a = 900 болса, яғ ни егер кү ш векторы жү ріп ө ткен жолғ а немесе жылдамдық қ а перпендикуляр бағ ытталса, кү штің элементар жұ мысы нө лге тең болады.
Бізге кинематикадан  екені белгілі (бұ л жердегі
екені белгілі (бұ л жердегі  - нү ктенің элемен- тар орын ауыстыру векторы), сондық тан элементар жұ мысты мына тү рде жазуғ а болады:
- нү ктенің элемен- тар орын ауыстыру векторы), сондық тан элементар жұ мысты мына тү рде жазуғ а болады:  ,
,
бұ л –  жә не
жә не  векторларының скалярлық кө бейтіндісі, яғ ни
векторларының скалярлық кө бейтіндісі, яғ ни
 . (3. 4. 13)
. (3. 4. 13)
(3. 4. 13) ө рнегін векторлардың проекциялары арқ ылы да жазуғ а болады:
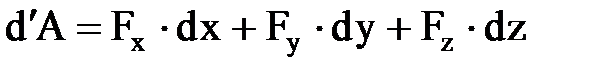 , (3. 4. 14)
, (3. 4. 14)
мұ ндағ ы x, y, z –  кү шінің тү су нү ктесінің координаталары.
кү шінің тү су нү ктесінің координаталары.
(3. 4. 11), (3. 4. 12), (3. 4. 13) жә не (3. 4. 14) ө рнектерінің бә рі кү штің элементар жұ мысы.
|
|
|


