 |
1.4 Статиканың негізгі теоремасы.
|
|
|
|
1. 4. 1 Кү шті параллель кө шіру туралы лемма.
Лемма. Дененің бірнү ктесіне тү скен кү шті ө зіне параллель етіп басқ а нү ктеге кө шіруге болады. Кү штің денеге ә сері ө згермеу ү шін кө шірілген кү шке моменті берілген кү штің жаң а нү ктеге қ атысты моментіне тең қ ос кү ш қ осу керек (дә лелдеуі дә ріс оқ ығ анда).
1. 4. 2 Статиканың негізгі теоремасы. Денеге  кү штер жү йесі ә сер етсін. Осы кү штердің геометриялық қ осындысы жү йенің бас векторы деп аталады:
кү штер жү йесі ә сер етсін. Осы кү штердің геометриялық қ осындысы жү йенің бас векторы деп аталады:
 (1. 4. 1)
(1. 4. 1)
Барлық кү штердің О нү ктесіне қ атысты моменттерінің геометриялық қ осындысы жү йенің О нү ктесіне қ атысты бас моменті деп аталады:
 . (1. 4. 2)
. (1. 4. 2)
Теорема. Абсолют қ атты денеге ә сер ететін кез келген кү штер жү йесін берілген О центріне келтіргенде жү йенің бас векторына тең, келтіру центріне тү скен бір кү шпен жә не моменті жү йенің бас моментіне тең бір қ ос кү шпен алмастыруғ а болады (дә лелдеуі дә ріс оқ ығ анда).
1. 4. 3 Тепе-тең дік шарттары. Теорема. Кез келген кү штер жү йесі тепе-тең дікте болу ү шін оның бас векторы мен бас моментінің нө лге тең болуы қ ажет жә не жеткілікті (дә лелдеусіз):  ,
,  . (1. 4. 3)
. (1. 4. 3)
1. 4. 4 Вариньон теоремасы. Теорема. Жинақ талатын кү штер жү йесінің тең ә серлікү шінің кез келген нү ктеге қ атысты моменті жү йе кү штерінің сол нү ктеге қ атысты моменттерінің геометриялық қ осындысына тең (дә лелдеусіз)
|
|
|
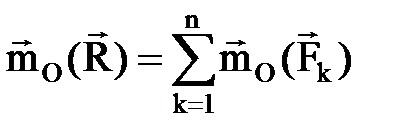 .
.
ТАҚ ЫРЫБЫ Жазық тық тағ ы кез келген кү штер жү йесі.
Дә ріс конспектісі
1. 5 Ә сер ету сызық тары бір жазық тық та жатып, кез келген тә ртіппен бағ ытталғ ан кү штер жазық тық тағ ы кез келген кү штер деп аталады. Мұ ндай кү штердің жазық тық тың кез келген нү ктесіне қ атысты моменттерінің векторлары осы жазық тық қ а перпендикуляр болып, бір біріне параллель бағ ытталады. Бұ л моменттерді бір бірінен таң басымен айыруғ а болады. Осығ ан байланысты жазық тық тағ ы кез келген кү штер жү йесі ү шін момент векторларының орнына олардың алгебралық шамалары қ арастырылады.
1. 5. 1
| А |
| В |
| С |
| О |

|

|

|
| h1 |
| h2 |
| 1. 10 сурет |
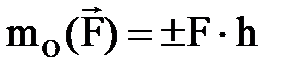 . (1. 5. 1)
. (1. 5. 1)
Егер кү ш денені сағ ат тіліне қ арсы бағ ытта бұ руғ а тырысса плюс таң басы алынады, сағ ат тілімен бағ ыттас бұ руғ а тырысса минус таң басы алынады. Егер кү штің ә сер ету сызығ ы нү ктеден ө тсе оның бұ л нү ктеге қ атысты моменті нө лге тең болады (1. 10 сурет):
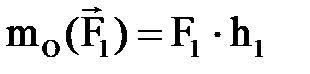 ,
,  ,
, 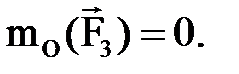
Қ ос кү штің алгебралық моменті депплюс немесе минус таң басымен алынғ ан оны қ ұ райтын кү штердің біреуінің модулі мен қ ос кү штің иінінің кө бейтіндісін айтады: 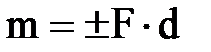 . (1. 5. 2)
. (1. 5. 2)
|
|
|
Егер қ ос кү ш денені сағ ат тіліне қ арсы бағ ытта бұ руғ а тырысса плюс таң басы алынады, ал сағ ат тілімен бағ ыттас бұ руғ а тырысса минус таң басы алынады (1. 11 а жә не ә суреттер):  ,
, 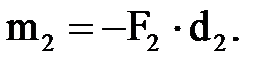
Қ ос кү штің моменті қ ос кү штің ә серін толық сипаттайтындық тан, кейде қ ос кү шті оның моментінің бағ ытын кө рсететін доғ аның тілімен бейнелейді (  ) (1. 11 б сурет).
) (1. 11 б сурет).

|

|
| d1 |
| m1 |
| m2 |

|
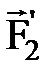
|
| d2 |
а) ә ) б)
1. 11 сурет
1. 5. 2 Жазық тық тағ ы кез келген кү штер жү йесінің бас векторы мен бас моменті. Жазық тық тағ ы кез келген кү штер жү йесі ү шін бас вектор барлық кү штердің геометриялық қ осындысы болады жә не декарттық координата жү йесінің екі ө сіне проекцияланады:  . (1. 5. 3)
. (1. 5. 3)
Бас вектордың шамасы (модулі) мына ө рнекпен: 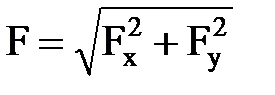 , (1. 5. 4)
, (1. 5. 4)
ал бағ ыты бағ ыттаушы косинустардың кө мегімен анық талады:
 (1. 5. 5)
(1. 5. 5)
Бұ л жағ дайда О нү ктесіне қ атысты бас момент барлық кү штердің О нү ктесіне қ атысты моменттерінің алгебралық қ осындысы болады: 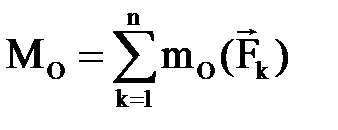 . (1. 5. 6)
. (1. 5. 6)
Егер денеге кү штермен қ атар қ ос кү штер ә сер етсе, олардың моменттері жү йенің бас моментіне қ осылады.
Кинематикағ а кіріспе. Нү кте кинематикасы.
Дә ріс конспектісі
2. 1 Кинематикағ а кіріспе. Кинематикада денелердің қ озғ алысы оғ ан ә сер ететін кү штерсіз, тек геометриялық тұ рғ ыдан зерттеледі. Дененің қ озғ алысы деп оның басқ а бір қ озғ алмайтын денеге қ атысты орын ауыстыруын айтады. Осы қ озғ алмайтын денеге координата жү йесі мен сағ атты байланыстырса, олар бірігіп санақ жү йесін қ ұ райды.
Теориялық механикада уақ ыт ү здіксіз ө згеріп отыратын шама болып есептеледі. Ол денелердің қ озғ алысына тә уелсіз жә не кез келген санақ жү йесі мен кең істіктің кез келген нү ктесінде бірдей, сондық тан, қ озғ алмайтын дененің жә не координата жү йесінің берілуімен шектелуге болады.
|
|
|
Жалпы жағ дайда қ озғ алатын дененің нү ктелері ә ртү рлі қ озғ алыс жасайды. Сондық тан алдымен нү кте қ озғ алысын қ арастырамыз.
2. 2 Нү кте кинематикасы. Кинематикада жү ріп ө ткен жолымен салыстырғ анда ө лшемі ә лде қ айда кіші денені нү кте деп атайды. Нү кте қ озғ алысының негізгі кинематикалық сипаттамаларына оның жылдамдығ ы мен ү деуі жатады. Нү кте кинематикасының негізгі мә селелері: 1) нү кте қ озғ алысының берілу ә дістерін анық тау, 2) нү ктенің қ озғ алыс заң ын біле отырып, оның жылдамдығ ы мен ү деуін анық тау.
2. 2. 1 Нү кте қ озғ алысының берілу ә дістері. Нү кте қ озғ алысы ү ш тү рлі ә діспен беріледі.
1. Векторлық ә діс. Бұ л ә дісте нү ктенің радиус-векторы 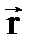 уақ ытқ а тә уелді функция ретінде беріледі (2. 1 сурет), яғ ни
уақ ытқ а тә уелді функция ретінде беріледі (2. 1 сурет), яғ ни
 (2. 2. 1)
(2. 2. 1)
Нү ктенің радиус-векторы координата жү йесінің бас нү ктесі болатын бір О нү ктесінен жү ргізіледі, бірақ координата жү йесінің берілуі нақ тыланбайды.
Уақ ыт ө згерген кездегі радиус-вектор ұ шының кең істіктегі геометриялық орындары нү ктенің траекториясы немесе радиус-вектордың годографы деп аталады. Егер нү ктенің траекториясы тү зу болса оның қ озғ алысы тү зу сызық ты қ озғ алыс, ал қ исық болса – қ исық сызық ты қ озғ алыс деп аталады.
2. Координаталық ә діс. Бұ л ә діс міндетті тү рдекоордината жү йесінің бері- луін талап етеді.  жү йесіндегі кез келген М нү ктенің орны оның
жү йесіндегі кез келген М нү ктенің орны оның 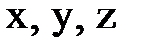 координаталарымен анық талады. Нү кте қ озғ алғ ан кезде оның координаталары ө згереді де уақ ытқ а тә уелді функциялар болады:
координаталарымен анық талады. Нү кте қ озғ алғ ан кезде оның координаталары ө згереді де уақ ытқ а тә уелді функциялар болады:
|
|
|


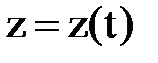 . (2. 2. 2)
. (2. 2. 2)
(2. 2. 2) – нү ктенің декарттық координата жү йесіндегі қ озғ алыс тең деулері. Нү кте траекториясын координаталық тү рде жазу ү шін (2. 2. 2) тең деулерінен уақ ытты жою қ ажет.
3. Табиғ и ә діс. Табиғ и ә дісті нү кте траекториясы алдын ала белгілі болғ ан жағ дайда пайдаланады. Бұ л ә дісте нү ктенің траекториясы, траектория бойындағ ы доғ аның бастапқ ы орны, қ озғ алыстың оң бағ ыты мен  доғ алық координатасы уақ ытқ а тә уелді функция ретінде беріледі, демек:
доғ алық координатасы уақ ытқ а тә уелді функция ретінде беріледі, демек:  (2. 2. 3)
(2. 2. 3)
Бұ л – қ озғ алысы табиғ и ә діспен берілген нү кте қ озғ алысының заң ы (тең деуі).
Сонымен, нү ктенің қ озғ алысын табиғ и ә діспен анық тау ү шін оның траекториясы, бас нү ктесі, траектория бойымен (2. 2. 3) тү рінде қ озғ алыс заң ы берілуіқ ажет екен.
Егер нү кте оң бағ ытта қ озғ алса доғ а дифференциалы 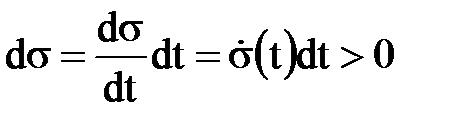 , ал теріс бағ ытта қ озғ алса бұ л дифференциал нө лден кіші болатынын айта кетейік.
, ал теріс бағ ытта қ озғ алса бұ л дифференциал нө лден кіші болатынын айта кетейік.
Нү ктенің жү ріп ө ткен жолы ә рқ ашан оң болдады, яғ ни  .
.
2. 2. 2 Нү ктенің жылдамдығ ы мен ү деуі. Нү кте қ озғ алысы ә ртү рлі ә діспен берілген кезде оның негізгі кинематикалық сипаттамалары қ алай анық талатынын қ арастырайық.
1. Векторлық ә діс. Нү ктенің t уақ ыттағ ы орны  радиус-векторымен, ал
радиус-векторымен, ал  уақ ыттағ ы орны
уақ ыттағ ы орны  радиус-векторымен анық талсын (2. 1 сурет). Осы векторлардың айырмасын
радиус-векторымен анық талсын (2. 1 сурет). Осы векторлардың айырмасын  арқ ылы белгілейік, яғ ни
арқ ылы белгілейік, яғ ни
| О |
| М |
| М1 |
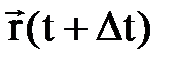
|

|

|
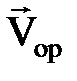
|

|
| 2. 1 сурет |
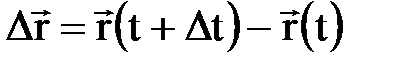 . (2. 2. 4)
. (2. 2. 4)
Бұ л вектор нү ктенің элементар  уақ ыттағ ы элементар орын ауыстыруы деп аталады.
уақ ыттағ ы элементар орын ауыстыруы деп аталады.
Элементар  орын ауыстыру векторы- ның элементар
орын ауыстыру векторы- ның элементар  уақ ытқ а қ атынасы нү ктенің орташа жылдамдығ ы деп аталады
уақ ытқ а қ атынасы нү ктенің орташа жылдамдығ ы деп аталады
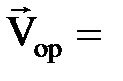
 (2. 2. 5)
(2. 2. 5)
Орташа жылдамдық векторы  векторы сияқ ты бағ ытталады.
векторы сияқ ты бағ ытталады.  нө лге ұ мтылғ ан кездегі
нө лге ұ мтылғ ан кездегі  мен
мен  қ атынасы шегі нү кте жылдамдығ ы деп аталады, яғ ни
қ атынасы шегі нү кте жылдамдығ ы деп аталады, яғ ни  (2. 2. 6)
(2. 2. 6)
|
|
|
Демек, нү кте жылдамдығ ының векторы оның радиус-векторынан уақ ыт бойынша алынғ ан бірінші туындығ а тең екен:  (2. 2. 7)
(2. 2. 7)
Жылдамдық векторы нү кте траекториясына жанама бойымен бағ ытталады (2. 1 сурет).
Дә л осындай  уақ ыттағ ы нү ктенің орташа ү деуінің:
уақ ыттағ ы нү ктенің орташа ү деуінің: 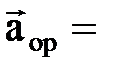
 (2. 2. 8)
(2. 2. 8)
жә не берілген уақ ыттағ ы нү кте ү деуінің ө рнектерін аламыз:
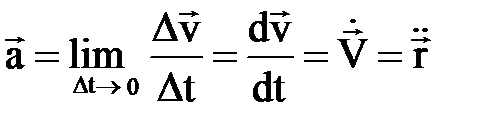 . (2. 2. 9)
. (2. 2. 9)
Демек, нү кте ү деуінің векторы оның жылдамдығ ының векторынан уақ ыт бойынша алынғ ан бірінші туындығ а немесе радиус-векторынан уақ ыт бойынша алынғ ан екінші туындығ а тең екен.
Нү кте ү деуінің векторы ә қ ашан нү кте траекториясының ойыс жағ ына қ арай бағ ытталады.
2. Координаталық ә діс. Нү кте қ озғ алысы координаталық ә діспен берілсе оның радиус-векторын декарттық координата жү йесінің тұ рақ ты  вектолары арқ ылы жазуғ а болады:
вектолары арқ ылы жазуғ а болады:  .
.
Осы радиус-вектордан (2. 2. 7) ө рнегін ескере отырып, нү кте жылдамдығ ы векторының декарттық координата ө стеріне проекцияларын аламыз:
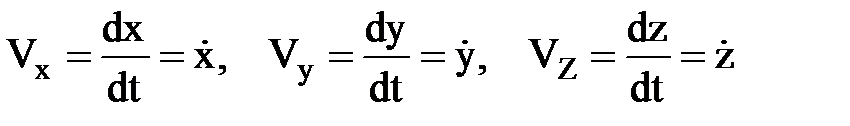 . (2. 2. 10)
. (2. 2. 10)
Жылдамдық тың сан шамасы мына ө рнекпен:  (2. 2. 11)
(2. 2. 11)
ал бағ ыты мына бағ ыттаушы косинустармен анық талады:
 . (2. 2. 12)
. (2. 2. 12)
Дә л осылай нү кте ү деуінің декарттық координата ө стеріне проекцияларын:
 , (2. 2. 13)
, (2. 2. 13)
нү кте ү деуінің сан шамасын:  (2. 2. 14)
(2. 2. 14)
жә не ү деу векторының бағ ыттаушы косинустарын аламыз:
 . (2. 2. 15)
. (2. 2. 15)
3. Табиғ и ә діс. Бұ л ә діспен берілген нү кте ү шін жылдамдық тың жалпы анық тамасына сә йкес тү рлендірулер жасағ аннан кейін, қ озғ алысы табиғ и ә діспен берілген нү кте жылдамдығ ы векторының ө рнегін аламыз:
 . (2. 2. 16)
. (2. 2. 16)
Нү кте жылдамдығ ы векторының жанама ө ске проекциясын анық тайтын  белгілеу ендірсек, онда жылдамдық векторы былай ө рнектеледі:
белгілеу ендірсек, онда жылдамдық векторы былай ө рнектеледі:
 . (2. 2. 17)
. (2. 2. 17)
Егер  > 0 болса жылдамдық векторы нү кте траекториясына жанама бойынша қ озғ алыстың оң бағ ытына қ арай (2. 5 а) сурет), ал
> 0 болса жылдамдық векторы нү кте траекториясына жанама бойынша қ озғ алыстың оң бағ ытына қ арай (2. 5 а) сурет), ал  < 0 болса – теріс бағ ытына қ арай бағ ытталады. Жылдамдық тың сан шамасы:
< 0 болса – теріс бағ ытына қ арай бағ ытталады. Жылдамдық тың сан шамасы:
 . (2. 2. 18)
. (2. 2. 18)
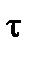
|

|
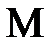
|

|
| - |
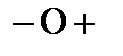
|
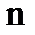
|
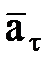
|
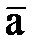
|

|
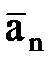
|
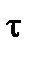
|
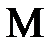 ә )
ә )
|

|
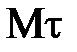 деп, бас нормаль ө сті
деп, бас нормаль ө сті 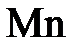 деп белгілейміз. Мtn жазық тығ ына нормаль ө сті
деп белгілейміз. Мtn жазық тығ ына нормаль ө сті  деп белгілеп, бинормаль ө сі деп атаймыз.
деп белгілеп, бинормаль ө сі деп атаймыз.
а)
2. 2 сурет
Нү кте ү деуін анық тау ү шін қ озғ алыс барысында 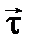 векторының бағ ытының ө згеретінін ескере отырып, оның жылдамдығ ы векторынан (2. 2. 17) бірінші туынды аламыз:
векторының бағ ытының ө згеретінін ескере отырып, оның жылдамдығ ы векторынан (2. 2. 17) бірінші туынды аламыз:
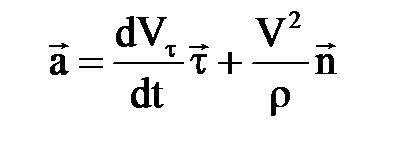 . (2. 2. 19)
. (2. 2. 19)
(2. 2. 19) - дан нү кте ү деуі векторының жанасушы жазық тық та жататынын жә не екі қ ұ раушыдан (жанама жә не нормаль) тұ ратынын кө реміз. Ү деудің жана- ма қ ұ раушысы траекторияғ а жанама бойынша, ал нормаль қ ұ раушысы – бас нор- маль бойымен траекторияның ойыс жағ ына қ арай бағ ытталғ ан (2. 2 ә ) сурет). Сонымен, нү ктенің толық ү деуінің векторы ү деудің жанама жә не нормаль қ ұ раушыларының геометриялық қ осындысына тең екен:  . (2. 2. 20)
. (2. 2. 20)
Ү деудің жанама ө ске проекциясы:  (2. 2. 21)
(2. 2. 21)
нү ктенің жанама (тангенциальдық ) ү деуі деп, ал бас нормальғ а проекциясы:
 , (2. 2. 22)
, (2. 2. 22)
нормальү деуі деп аталады, мұ ндағ ы r – траекторияның қ исық тық радиусы.
Нү ктенің толық ү деуінің сан шамасы (модулі):  . (2. 2. 23)
. (2. 2. 23)
2. 2. 3 Нү кте қ озғ алысының кейбір дербес жағ дайлары. Нү кте қ озғ алысының бірнеше дербес жағ дайларын қ арастырып, оның негізгі кинематикалық сипаттамаларын анық тайық..
1. Нү ктенің тү зу сызық ты қ озғ алысы. Тү зу сызық ты қ озғ алыстағ ы нү ктенің қ исық тық радиусы шексіздікке тең. Мұ ндай қ озғ алыста (2. 2. 22) ө рнегінен нормаль ү деудің нө лге айналатынын, ал толық ү деудің жанама ү деуге тең екенін кө реміз: 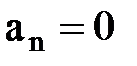 , демек
, демек 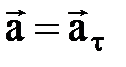 .
.
Бұ л жағ дайда жылдамдық тың тек шамасы ғ ана ө згереді, демек жанама ү деужылдамдық шамасының ө згеруін сипаттайды.
2. Бірқ алыпты қ озғ алыс. Қ озғ алыс барысында жылдамдық шамасы ә рқ ашан тұ рақ ты болатын қ озғ алыс бірқ алыпты қ озғ алыс деп аталады. Мұ ндай қ озғ алыс кезінде (2. 2. 21) ө рнегіне сә йкес жанама ү деунө лге тең , ал толық ү деу тек нормаль ү деуге тең болады: 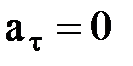 , демек
, демек 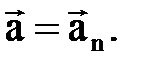
Мұ ндай қ озғ алыста жылдамдық тың тек бағ ыты ғ ана ө згереді, сондық тан нормаль ү деужылдамдық бағ ытының ө згеруін сипаттайды.
3. Нү ктенің бірқ алыпты тү зу сызық ты қ озғ алысы. Нү кте бір мезгілде бірқ алыпты жә не тү зу сызық ты қ озғ алыс жасағ андық тан оның жанама жә не нормаль ү деулері бір мезгілде нө лге айналады. Демек, мұ ндай қ озғ алыста нү ктенің толық ү деуі де нө лге тең болады:  жә не
жә не  , демек
, демек 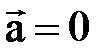 .
.
Бірқ алыпты жә не тү зу сызық ты қ озғ алыстағ ы нү кте жылдамдығ ының шамасы да, бағ ыты да тұ рақ ты болады.
4. Бірқ алыпты айнымалы қ озғ алыс. Қ озғ алыс барысында жанама ү деу ә рқ ашан тұ рақ ты болатын қ озғ алыс ( 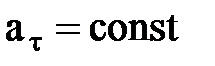 ) бірқ алыпты айнымалық озғ а- лыс деп аталады. Бірқ алыпты айнымалы қ озғ алыс кезіндегі жылдамдық тың ө згеру заң ы:
) бірқ алыпты айнымалық озғ а- лыс деп аталады. Бірқ алыпты айнымалы қ озғ алыс кезіндегі жылдамдық тың ө згеру заң ы:  , ал нү ктенің бірқ алыпты айнымалы қ озғ алы- сының заң ы:
, ал нү ктенің бірқ алыпты айнымалы қ озғ алы- сының заң ы:  .
.
Егер 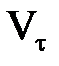 мен
мен 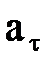 таң балары бірдей болса, қ озғ алыс бірқ алыпты ү демелі, ал ә ртү рлі болса – бірқ алыпты кемімелі болады.
таң балары бірдей болса, қ озғ алыс бірқ алыпты ү демелі, ал ә ртү рлі болса – бірқ алыпты кемімелі болады.
Қ атты дененің қ арапайым қ озғ алыстары. Қ атты дене кинематикасы- ның мә селелерін екіге бө луге болады: 1) бү кіл дененің қ озғ алыс заң ын алу мен оның кинематикалық сипаттамаларын анық тау; 2) дененің жеке нү ктелерінің қ озғ алысының кинематикалық сипаттамаларын анық тау. Қ атты дененің ілгері- лемелі қ озғ алысы мен тұ рақ ты ө сті айналуы дененің қ арапайым қ озғ алыстарына жатады.
2. 3. 1 Қ атты дененің ілгерілемелі қ озғ алысы. Дене қ озғ алғ анда оның бойындағ ы бір тү зу кесінді ө зіне ө зі параллель болып отырса, дененің қ озғ алы- сы ілгерілемелі қ озғ алыс деп аталады. Мұ ндай жағ дайда дене нү ктелерінің қ озғ алысы келесі теоремамен анық талады: ілгерілемелі қ озғ алыстағ ы дененің барлық нү ктелері бірдей траекториялар сызады, берілген уақ ытта барлық нү ктелерінің жылдамдық тары мен ү деулері бірдей болады.
 ,
,  . (2. 3. 1)
. (2. 3. 1)
Сонымен, ілгерілемелі қ озғ алыстағ ы дененің тек бір нү ктесінің қ озғ алысын ғ ана қ арастыруғ а болады, ал басқ а нү ктелері дә л осы нү кте сияқ ты қ озғ алады да, дене кинематикасының мә селесі нү кте кинематикасының мә селесіне тіреледі.
2. 3. 2 Қ атты дененің тұ рақ ты ө сті айкала қ озғ алуы. Қ озғ алыстағ ы дененің кем дегенде екі нү ктесі (А жә не В) қ озғ алмайтын болса, онда қ озғ алыс қ атты дене- нің тұ рақ ты ө сті айнала қ озғ алуы деп аталады (2. 3 сурет). Қ озғ алмайтын екі нү ктені қ осатын тү зу айналу ө сі деп аталады. Айналу ө сінде жататын нү ктелердің барлығ ы қ озғ алмайды. Ал айналу ө сінде жатпайтын нү ктелер центрлері осы ө сте жататын, жазық тық тары айналу ө сіне перпендикуляр шең берлер сызады.
Дененің мұ ндай қ озғ алысын оның j айкалу бұ рышымен сипаттауғ а болады (2. 4 сурет): 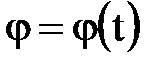 , (2. 3. 2)
, (2. 3. 2)
бұ л - дененің тұ рақ ты ө сті айкалу заң ы, мұ ндағ ы j - радианмен ө лшене- тін дененің айналу бұ рышы.
Қ атты дененің айналмалы қ озғ алысының негізгі кинематикалық сипаттамала- рына бұ рыштық жылдамдық пен бұ рыштық ү деу жатады. Дененің бұ рыштық жылдамдығ ының алгебралық шамасы айналу бұ рышынан уақ ыт бойынша алынғ ан бірінші туындығ а тең. Осы шаманың модулі д ененің бұ рыштық жыл-
U AAYACAAAACEAiI1RtuAAAAAIAQAADwAAAGRycy9kb3ducmV2LnhtbEyPQUvDQBCF74L/YRnBm90k NrXETEop6qkItkLpbZudJqHZ3ZDdJum/dzzpZZjhPd58L19NphUD9b5xFiGeRSDIlk43tkL43r8/ LUH4oKxWrbOEcCMPq+L+LleZdqP9omEXKsEh1mcKoQ6hy6T0ZU1G+ZnryLJ2dr1Rgc++krpXI4eb ViZRtJBGNZY/1KqjTU3lZXc1CB+jGtfP8duwvZw3t+M+/TxsY0J8fJjWryACTeHPDL/4jA4FM53c 1WovWoQkTbhLQODJcvqy4OWEMJ8vY5BFLv8XKH4AAAD//wMAUEsBAi0AFAAGAAgAAAAhALaDOJL+ AAAA4QEAABMAAAAAAAAAAAAAAAAAAAAAAFtDb250ZW50X1R5cGVzXS54bWxQSwECLQAUAAYACAAA ACEAOP0h/9YAAACUAQAACwAAAAAAAAAAAAAAAAAvAQAAX3JlbHMvLnJlbHNQSwECLQAUAAYACAAA ACEAmyICZRoMAAC9igAADgAAAAAAAAAAAAAAAAAuAgAAZHJzL2Uyb0RvYy54bWxQSwECLQAUAAYA CAAAACEAiI1RtuAAAAAIAQAADwAAAAAAAAAAAAAAAAB0DgAAZHJzL2Rvd25yZXYueG1sUEsFBgAA AAAEAAQA8wAAAIEPAAAAAA== ">
| j |
| Dj |
| z |
| O |
| 2. 4 сурет |
| А |
| В |
| айналу ө сі |
| 2. 3 сурет |
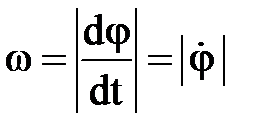 . (2. 3. 3)
. (2. 3. 3)
Бұ рыштық жылдамдық тың ө л- шем бірлігі: [рад/с, 1/с,  ].
].
Дененің бұ рыштық ү деуі- нің алгебралық шамасы бұ рыш- тық жылдамдық тың алгебралық шамасынан уақ ыт бойынша алынғ ан бірінші туындығ а неме- се айналу бұ рышынан алынғ ан екінші туындығ а тең. Осы шама- ның модулі дененің бұ рыштық ү деуі деп аталады:
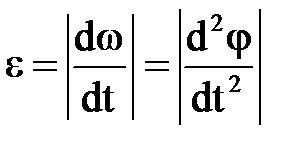 немесе
немесе  (2. 3. 4)
(2. 3. 4)
Бұ рыштық ү деудің ө лшем бірлігі: [рад/с2 ] немесе [1/с2,  ].
].
2. 3. 3 Қ атты дененің айналмалы қ озғ алысының дербес жағ дайлары. Қ атты дененің айналмалы қ озғ алысының екі дербес жағ дайын қ арастырамыз.
Бірқ алыпты айналу кезінде дененің бұ рыштық жылдамдығ ы тұ рақ ты болады (w = const). Бұ рыштық жылдамдық тың алгебралық шамасы тек таң бамен ерекшеленетіндіктен  =const болады. Кө п жағ дайда дене бірқ алыпты айналғ ан- да бұ рыштық жылдамдық тың орнына
=const болады. Кө п жағ дайда дене бірқ алыпты айналғ ан- да бұ рыштық жылдамдық тың орнына  минуттік айналым саны қ арастырылады. Минуттік айналым саны мен бұ рыштық жылдамдық тың арасындағ ы байланыс:
минуттік айналым саны қ арастырылады. Минуттік айналым саны мен бұ рыштық жылдамдық тың арасындағ ы байланыс:
 .
.
Қ атты дененің бірқ алыпты айналу заң ы: 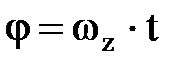 . (2. 3. 5)
. (2. 3. 5)
Бірқ алыпты айнымалы айналу кезінде дененің бұ рыштық ү деуі тұ рақ ты болады (  =const). Бұ л жағ дайда бұ рыштық ү деудің алгебралық шамасы да тұ рақ ты
=const). Бұ л жағ дайда бұ рыштық ү деудің алгебралық шамасы да тұ рақ ты  =const.
=const.
Бірқ алыпты айнымалы айналуда бұ рыштық жылдамдық тың ө згеру заң ы:
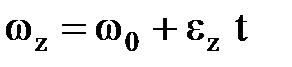 , (2. 3. 6)
, (2. 3. 6)
бірқ алыпты айнымалы айналу заң ы:  . (2. 3. 7)
. (2. 3. 7)
Егер  пен
пен 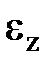 бір таң балы болса, айналу бірқ алыпты ү демелі, ал қ арсы болса – бірқ алыпты кемімелі деп аталады.
бір таң балы болса, айналу бірқ алыпты ү демелі, ал қ арсы болса – бірқ алыпты кемімелі деп аталады.
2. 3. 4 Айналмалы қ озғ алыстағ ы қ атты дене нү ктелерінің жылдамдық тары мен ү деулері. 2. 5-суретте Oz ө сін айналатын дененің М нү ктесі сызатын шең бер бейнеленген. Осы нү кте жылдамдығ ының жанама ө ске проекциясын былай жазуғ а болады:  , (2. 3. 8)
, (2. 3. 8)
мұ ндағ ы h - М нү ктесі сызатын шең бердің радиусы. Сонда нү кте жылдамды- ғ ының шамасы (сызық тық жылдамдық ) мына ө рнекпен анық талады:
 . (2. 3. 9)
. (2. 3. 9)
Нү кте жылдамдығ ының векторы осы шең берге жанама бойымен (2. 5 сурет) бұ рыштық жылдамдық тың бағ ытына қ арай бағ ытталғ ан.
М нү ктесінің жылдамдығ ының векторын бұ рыштық жылдамдық тың векторы мен нү ктенің радиус-векторының векторлық кө бейтіндісі арқ ылы да жазуғ а болады (2. 5 а) сурет): 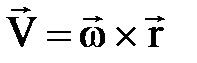 . (2. 3. 10)
. (2. 3. 10)
М нү ктесінің ү деуін анық тау ү шін оның жылдамдығ ының векторынан (1. 3. 10) уақ ыт бойынша туынды алу керек, сонда:
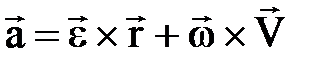 . (2. 3. 11)
. (2. 3. 11)
(2. 3. 11) ө рнектің бірінші қ осылғ ышы нү кте ү деуі векторының айналмалы, ал екіншісі – центрге тартқ ыш қ ұ раушысы деп аталады. Сонымен, айналмалы қ озғ алыстағ ы дененің Мнү ктесінің ү деуінің векторы оның айналмалы жә не центрге тартқ ыш қ ұ раушыларының геометриялық қ осындысына тең:
| М |
| e |
| w |

|
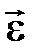
|

|

|
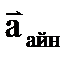
|
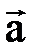
|
| x |
| y |
| z |
| O |
| a |
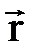
|
| h |
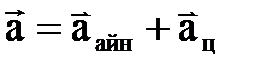 . (2. 3. 12)
. (2. 3. 12)
| M |
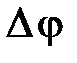
|
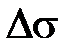
|
| h |
| e |
| w |

|

|
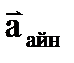
|
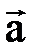
|
ә ) а)
2. 5 сурет
М нү ктесі ү деуінің қ ұ раушыларының абсолют шамалары нү ктенің айналмалы жә не центрге тартқ ыш ү деулері деп аталады жә не мына ө рнектермен анық талады:
|
|
|


