 |
Күштің кез келген М0М1 орын ауыстырудағы жұмысы элементар жұмыс- тан осы орын ауыстыру бойынша алынған интегралға тең.
|
|
|
|
(3. 4. 11) – (3. 4. 14) ө рнектеріне сә йкес кү ш жұ мысының тө рт тү рлі ө рнегі:
 , (3. 4. 15)
, (3. 4. 15)
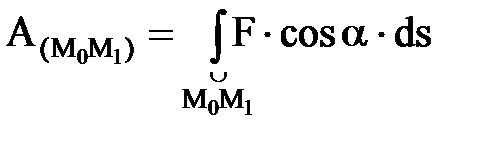 , (3. 4. 16)
, (3. 4. 16)
 , (3. 4. 17)
, (3. 4. 17)
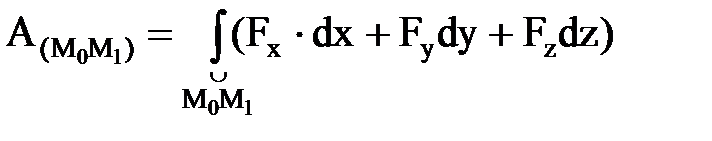 . (3. 4. 18)
. (3. 4. 18)
Барлық жағ дайларда интеграл М0М1 қ исығ ы бойымен алынады.
Уақ ыт бірлігі аралығ ында орындалатын кү штің жұ мысын анық тайтын шама қ уат деп аталады. Егер жұ мыс бірқ алыпты орындалса, қ уат
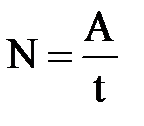 ,
,
мұ ндағ ы t – жұ мыс жасалатын уақ ыт. Жалпы жағ дайда
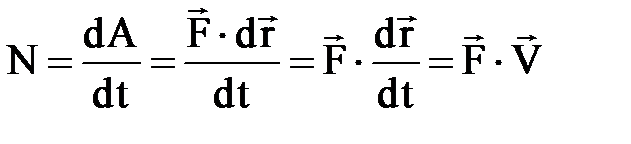 , (3. 4. 19)
, (3. 4. 19)
демек, кү ш қ уаты  кү ші мен нү кте жылдамдығ ының
кү ші мен нү кте жылдамдығ ының  скалярлық кө бейтіндісіне тең.
скалярлық кө бейтіндісіне тең.
3. 4. 5 Жұ мысты есептеу мысалдары. Есеп шығ арғ анда қ олданатын кү ш жұ мысын санау ө рнектерін алайық.
1. Ауырлық кү шінің жұ мысы. Ауырлық кү ші 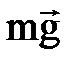 ә сер ететін нү кте бастап- қ ы М0 (x0, y0, z0) орнынан М1 (x1, y1, z1)-ге орын ауыстырсын. Ауырлық кү шінің жұ мысын (3. 4. 18) ө рнегімен есептейік, сонда
ә сер ететін нү кте бастап- қ ы М0 (x0, y0, z0) орнынан М1 (x1, y1, z1)-ге орын ауыстырсын. Ауырлық кү шінің жұ мысын (3. 4. 18) ө рнегімен есептейік, сонда
 , (3. 4. 20)
, (3. 4. 20)
 - нү ктенің орын ауыстыру биіктігі.
- нү ктенің орын ауыстыру биіктігі.
Демек, ауырлық кү шінің жұ мысы плюс не минус таң бамен алынғ ан ауырлық кү ші модулі мен вертикаль орын ауыстырудың кө бейтіндісіне тең екен. Плюс таң басы нү кте тө мен орын ауыстырғ анда, ал минус таң басы нү кте жоғ ары қ арай орын ауыстырғ анда алынады.
2.
| x |

|
| М |
| O |

|

|
| М1 |
| М0 |
| 3. 4сурет |
 –деформацияланбағ ан серіппенің ұ зындығ ы). Егер жү кті О тепе-тең дік орнынан серіппенің ұ зындығ ы
–деформацияланбағ ан серіппенің ұ зындығ ы). Егер жү кті О тепе-тең дік орнынан серіппенің ұ зындығ ы  болатындай етіп созсақ, серіппе
болатындай етіп созсақ, серіппе 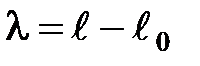 -ге созылады да, жү кке О нү ктесіне бағ ытталғ ан
-ге созылады да, жү кке О нү ктесіне бағ ытталғ ан 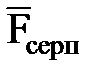 серпімділік кү ші ә сер етеді. 3. 5 суретінен
серпімділік кү ші ә сер етеді. 3. 5 суретінен  екенін кө реміз, сондық тан серпімділік кү шін былай жазуғ а болады:
екенін кө реміз, сондық тан серпімділік кү шін былай жазуғ а болады: |
|
|
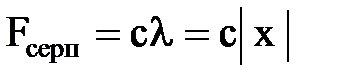 жә не
жә не 
мұ ндағ ы с – серіппенің серпімділік коэффициенті.
Жү к бастапқ ы М0(х0) орнынан М1(х1)-ге орын ауыстырғ андағ ы серпімділік кү шінің жұ мысын,  деп алып, (3. 4. 18) тең деуінен анық таймыз:
деп алып, (3. 4. 18) тең деуінен анық таймыз:
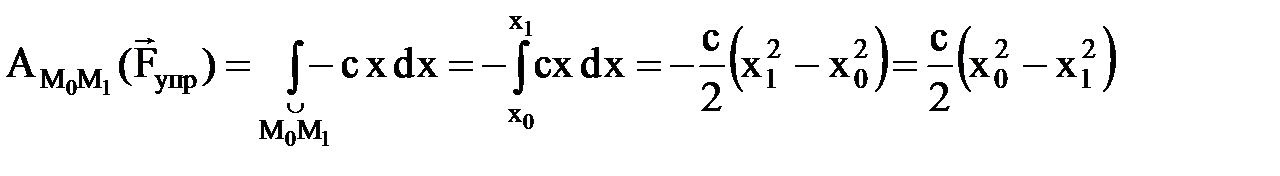 .
.
Бұ л ө рнектегі х0 серіппенің бастапқ ы деформациясы l0, ал х1 – соң ғ ы деформациюсы l1. Сондық тан серпімділік кү шінің жұ мысын мына тү рде жазуғ а болады:
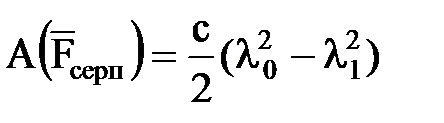 . (3. 4. 21)
. (3. 4. 21)
Демек, серпімділік кү шінің жұ мысы серіппенің серпімділік коэффициенті мен бастапқ ы жә не соң ғ ы деформациялар айырмасы квадратының кө бейтіндісінің жартысына тең.
(3. 4. 21) ө рнегі М нү ктесінің орын ауыстыруы тү зу сызық ты болмаса да орын алады. Бұ лсерпімділік кү шінің жұ мысы нү кте траекториясының тү ріне тә уелді емес екендігін кө рсетеді.
3. Ү йкеліс кү шінің жұ мысы. Егер нү кте кедір-бұ дырлы жазық тық пен қ озғ алса, оғ ан ә сер ететін ү йкеліс кү шінің модулі f N болады. Бұ л жерде f – ү йкеліс коэффициенті, ал N – жазық тық тың нормаль реакциясы. Ү йкеліс кү ші қ озғ алысқ а қ арсы бағ ытталғ андық тан  жә не (3. 4. 15) ө рнегі бойынша
жә не (3. 4. 15) ө рнегі бойынша
 . (3. 4. 22)
. (3. 4. 22)
Егер ү йкеліс кү ші тұ рақ ты болса, онда
 , (3. 4. 23)
, (3. 4. 23)
|
|
|
s – нү кте қ озғ алатын М0М1 қ исығ ы доғ асының ұ зындығ ы.
Сонымен, сырғ анау ү йкелісі кү шінің жұ мысы ә рқ ашан таң балы жә не нү ктенің жү ріп ө ткен жолына тә уелді екен.
4. Тартылыс кү шінің жұ мысы. Жер беті маң ындағ ы нү ктеге ә сер ететін  тартылыс кү шінің жұ мысы мына ө рнекпен анық талады:
тартылыс кү шінің жұ мысы мына ө рнекпен анық талады:
 . (3. 4. 24)
. (3. 4. 24)
Егер 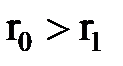 болса бұ л жұ мыс оң таң балы, ал
болса бұ л жұ мыс оң таң балы, ал  болса бұ л жұ мыс теріс таң балы болады. Тартылыс кү шінің жұ мысы нү ктенің траекториясына тә уелді емес.
болса бұ л жұ мыс теріс таң балы болады. Тартылыс кү шінің жұ мысы нү ктенің траекториясына тә уелді емес.
3. 4. 6 Нү ктенің кинетикалық энергиясы жә не оның ө згеруі туралы теорема. Нү кте қ озғ алысының келесі динамикалық сипаттамасы – кинетикалық энергия.
Нү ктенің кинетикалық энергиясы деп оның массасы мен жылдамдығ ының квадратының кө бейтіндісінің жартысына тең скаляр шаманы айтады – 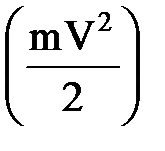 .
.
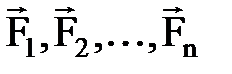 кү штер ә сер ететін М материялық нү ктені қ арастырайық. Ол қ исық бойымен
кү штер ә сер ететін М материялық нү ктені қ арастырайық. Ол қ исық бойымен  жылдамдық пен бастапқ ы М0 орнынан,
жылдамдық пен бастапқ ы М0 орнынан,  жылдамдық пен М1-ге орын ауыстырсын.
жылдамдық пен М1-ге орын ауыстырсын.
Нү кте динамикасының негізгі тең деуін (Ньютонның екінші заң ы) қ олданып, келесі тең деуді алуғ а болады: 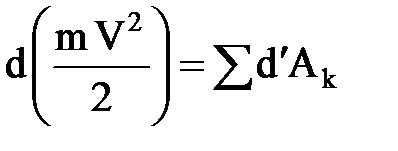 , (3. 4. 25)
, (3. 4. 25)
бұ л тең деу нү ктенің кинетикалық энергиясының ө згеруі туралы теореманың дифференциалдық тү рі деп аталады: нү ктенің кинетикалық энергиясының толық дифферен- циалы нү ктеге ә сер ететін барлық кү штердің элементар жұ мыстарының қ осындысына тең.
Бұ л теоремадан 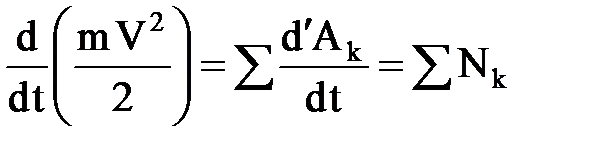 (3. 4. 26)
(3. 4. 26)
екенін кө реміз, яғ ни нү ктенің кинетикалық энергиясының толық дифференциалы нү ктеге ә сер ететін барлық кү штердің қ уаттарының қ осындысына тең.
Нү кте бастапқ ы М0 орыннан М1-ге орын ауыстырғ анда оның бастапқ ы жылдамдығ ы  -ден
-ден  -ге дейін ө згеретінін ескеріп, (3. 4. 25) тең деуін интегралдаймыз, сонда:
-ге дейін ө згеретінін ескеріп, (3. 4. 25) тең деуін интегралдаймыз, сонда:
 . (3. 4. 27)
. (3. 4. 27)
(3. 4. 27) тең деуі нү ктенің кинетикалық энергиясының ө згеруі туралы теореманың интералдық (шекті) тү рін береді: нү кте шекті орын ауыстырғ андағ ы оның кинетикалық энергиясының ө згеруіосы орын ауыстыруда нү ктеге ә сер ететін барлық кү штердің жұ мыстарының алгебралық қ осындысына тең.
|
|
|
3. 5 Материялық нү кте ү шін Даламбер принципі. Материялық нү кте ү шін Даламбер принципі нү кте динамикасының есептерін статиканың қ арапайым ә дістерімен шығ аруғ а мү мкіндік береді.
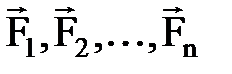 актив кү штері мен
актив кү штері мен 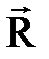 реакция кү ші ә сер ететін материялық нү ктені қ арастырайық. Бұ л нү кте ү шін динамиканың негізгі заң ы:
реакция кү ші ә сер ететін материялық нү ктені қ арастырайық. Бұ л нү кте ү шін динамиканың негізгі заң ы:  .
.
Осы заң ды былай жазайық:
 . (3. 5. 1)
. (3. 5. 1)
Мынадай белгілеу енгізейік:
 . (3. 5. 2)
. (3. 5. 2)
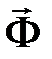 векторы материялық нү ктенің инерция кү ші деп аталады. Оның модулі нү ктенің массасы мен ү деуінің кө бейтіндісіне тең, ал бағ ыты ү деу векторына қ арсы.
векторы материялық нү ктенің инерция кү ші деп аталады. Оның модулі нү ктенің массасы мен ү деуінің кө бейтіндісіне тең, ал бағ ыты ү деу векторына қ арсы.
(3. 5. 2) ескерсек (3. 5. 1) тең деуі мынадай тү рге келеді:
 . (3. 5. 3)
. (3. 5. 3)
(3. 5. 3) ө рнегі материялық нү кте ү шін Даламбер принципі болады: қ озғ а- лыстағ ы материялық нү ктеге ә сер ететін актив кү штер, реакция кү ші жә не инерция кү ші тең естірілген кү штер жү йесін қ ұ райды. Бірақ материялық нү ктеге тек актив кү штер мен реакция кү ші ғ ана ә сер ететін ескеру керек, ал инерция кү ші нү ктеге ә сер етпейді, сондық тан да ол жасанды кү ш.
|
|
|


