2.4 . Нүктенің күрделі қозғалысы.

2. 5. 1  Нү ктенің кү рделі қ озғ алысының негізгі анық тамалары. Кө птеген есептерде нү ктенің (дененің ) қ озғ алысын екі немесе одан да кө п координата жү йелеріне қ атысты қ арастыруғ а тура келеді. Бұ л жағ дайда нү кте қ озғ алысы кү рделі қ озғ алыс деп аталады. Негізгі жү йені (О₁x₁y₁z₁) шартты тү рде қ озғ алмай- ды, ал екінші жү йені (Oxyz) оғ ан қ атысты еркін қ озғ алады деп алып, нү ктенің екі жү йеге қ атысты қ озғ алысын қ арастырайық.

Келесі анық тамаларды ендіреміз.

1. М нү ктесінің қ озғ алмайтын О₁x₁y₁z₁ координата жү йесіне қ атысты қ озғ алысы нү ктенің абсолют қ озғ алысы деп аталады.

2. М нү ктесінің қ озғ алатын Oxyz координата жү йесіне қ атысты қ озғ алысы нү ктенің салыстырмалы қ озғ алысы деп аталады.

3. Қ озғ алатын Oxyz  жү йесінің қ озғ алмайтын О₁x₁y₁z₁ жү йесіне қ атысты қ озғ алысы М нү ктесі ү шін тасымал қ озғ алыс деп аталады.

Мұ ндай қ озғ алыстың кинематикалық сипаттамаларын анық тау кезінде қ озғ а- латын жү йеде берілген вектордан туынды алу қ ажет болады. Сондық тан қ озғ ала- тын жү йеде берілген  векторын қ арастырайық. Қ озғ алатын жү йеде берілген вектордың абсолют туындысы оның салыстырмалы туындысы мен қ озғ ала- тын жү йенің бұ рыштық жылдамдығ ының осы вектормен векторлық кө бейтіндісінің қ осындысына тең:

          немесе 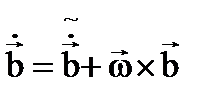           .           (2. 5. 1)

2. 5. 2 Жылдамдық тарды қ осу туралы теорема. Oxyz жү йесі негізгі қ озғ ал- майтын жү йе ретінде таң далғ ан О₁x₁y₁z₁ координата жү йесіне қ атысты еркін қ озғ алатын болсын (2. 18 сурет). Кез келген М нү ктесінің қ озғ алысын жоғ арыда айтылғ ан ә дістермен қ озғ алмайтын жү йеге де, қ озғ алатын жү йеге де қ атысты қ арастыруғ а болады. Осы координата жү йелеріне қ атысты нү кте жылдамдық тары арасындағ ы байланысты табайық. Нү ктенің кү рделі қ озғ алысында пайда болатын жылдамдық тардың анық тамаларын ендіреміз.

1.

z1

О1

О

x1

y1

z

y

x

M

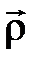
2. 15 сурет

М нү ктесінің қ озғ алмайтын О₁x₁y₁z₁ координата жү йесіне қ атысты жылдам- дығ ы абсолют жылдамдық  деп аталады.

2. М нү ктесінің қ озғ алатын Oxyz коорди- ната жү йесіне қ атысты жылдамдығ ы салыс- тырмалы жылдамдық ( 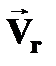) деп аталады.

3.   М нү ктесінің тасымал жылдамдығ ы ( ) деп берілген уақ ытта қ озғ алатын жү йе- нің қ озғ алыстағ ы нү ктемен сә йкес келетін нү ктесінің жылдамдығ ын айтады.

2. 15 суретте 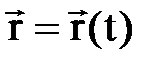 радиус-векторы М нү ктесінің О₁x₁y₁z₁ қ озғ алмайтын координа- та жү йесіндегі орнын,  радиус-векторы қ озғ алатын Oxyz координата жү йесі бас нү ктесінің О₁x₁y₁z₁ қ озғ алмай- тын координата жү йесіндегі орнын, ал  радиус-векторы М нү ктесінің қ озғ алатын Oxyz координата жү йесіндегі орнын анық тайды. Осы суреттен

                                                 ,                                               (2. 5. 2)

мұ ндағ ы  - қ озғ алатын координата жү йесінде берілген вектор.

Осы тең діктен кү рделі қ озғ алыстағ ы нү кте ү шін жылдамдық тарды қ осу тура- лы теореманы алуғ а болады: нү ктенің абсолют жылдамдығ ы оның салыстыр- малы жә не тасымал жылдамдық тарының геометриялық қ осындысына тең:  

                                                   .                                            (2. 5. 3)

Мұ ндағ ы 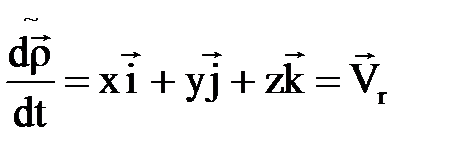                                                                  (2. 5. 4)

М нү ктесінің салыстырмалы жылдамдығ ы, ал 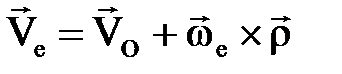              (2. 5. 5)

тасымал жылдамдығ ы.                                                         

Нү ктенің салыстырмалы жылдамдығ ын табу ү шін қ озғ алатын жү йені ойша тоқ тату керек. Нү ктенің тасымал жылдамдығ ын табу ү шін нү ктенің салыстырмалы қ озғ алысын ойша тоқ тату қ ажет.

2. 5. 3 Кориолис теоремасы (ү деулерді қ осу туралы теорема). Кориолис теоре- масы кү рделі қ озғ алыстағ ы нү кте ү деулерінің арасындағ ы байланысты береді.

Нү ктенің абсолют ү деуін табу ү шін (2. 5. 4) пен (2. 5. 5) ө рнектерін ескере отырып (2. 5. 3) тең деуін уақ ыт бойынша дифференциалдаймыз. Нә тижесінде Кориолис теоремасын аламыз: 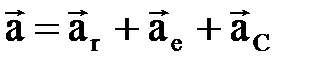                        .                 (2. 5. 6)

М

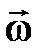
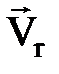
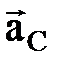
М

Теорема. Нү ктенің абсолют ү деуі салыстырмалы, тасымал жә не кориолис ү деулерінің геометриялық қ осындысына тең.

 

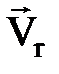
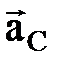
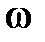
                        2. 16 сурет                                                      2. 17 сурет

Салыстырмалы ү деу:      ,                               (2. 5. 7)

тасымал ү деу:                      ,                          (2. 5. 8)

жә не кориолис ү деуі: 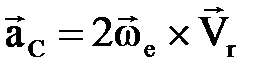                       .                                      (2. 5. 9)

Нү ктенің кориолис ү деуі. Екі вектордың векторлық кө бейтіндісі болғ ан- дық тан, бұ л ү деудің модулі мына ө рнекпен анық талады

                                       .                           (2. 5. 10)

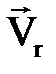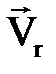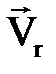Оның бағ ыты векторлық кө бейтіндінің бағ ытымен анық талады, яғ ни  векторы  мен  векторлары арқ ылы ө тетін жазық тық қ а перпендикуляр бағ ытталып, ұ шынан қ арағ анда -дан -ге қ арай қ ысқ а жолмен бұ рылу сағ ат тіліне қ арсы болып кө ріну керек (2. 16 сурет). Егер  мен  векторлары бір жазық тық та жатпаса, онда  векторын ө зіне ө зін параллель етіп 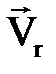 векторының басына ойша кө шіріп, жоғ арыда айтылғ ан ережені қ олданғ ан ың ғ айлы.

Кейде кориолис ү деуінің бағ ытын табуды Н. Е. Жуковский ережесі жең ілдетеді: 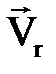 салыстырмалы жылдамдық тың векторын қ озғ алатын жү йенің  бұ рыштық жылдамдығ ына перпендикуляр жазық тық қ а проекциялап, осы жазық тық та -ның бағ ытына қ арай 90^о-қ а бұ ру керек (2. 17 сурет).

(2. 5. 10) ө рнегі бойынша кориолис ү деуі нө лге тең болатын жағ дайлар:     

· , яғ ни қ озғ алатын координата жү йесі ілгерілемелі қ озғ алғ анда;

·  қ озғ алатын координата жү йесінің  бұ рыштық жылдамдығ ы нү ктенің 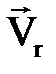 салыстырмалы жылдамдығ ына параллель болғ анда;

 нү ктенің салыстырмалы жылдамдығ ы  болғ анда

 

 

2. 5                       Қ атты дененің жазық -параллель қ озғ алысы. Қ озғ алыстағ ы дененің барлық нү ктелері қ озғ алмайтын бір (Ж) жазық тығ ына паралель жазық тық тарда орын ауыстыратын болса, дененің қ озғ алысы жазық немесе жазық -параллель қ озғ алыс деп аталады.

Техникада дененің жазық -параллель қ озғ алысының мә ні зор. Себебі кө пшілік механизмдер мен машиналардың буындары дә л осы қ озғ алысты жасайды.

2. 4. 1 Қ атты дененің жазық -параллель қ озғ алысының тең деулері. Дененің жазық -параллель қ озғ алысын қ арастырайық (2. 6 сурет). Дененің барлық нү ктеле- рі (Ж) жазық тығ ына параллель жазық тық тарда орын ауыстырсын. Сонда,  қ имасы қ озғ алмайтын (Ж) жазық тығ ына параллель қ озғ алады. Дене бойымен (Ж) жазақ тығ ына перпендикуляр жү ргізілген кез келген 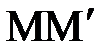 тү зуі ілгерілемелі қ озғ алыс жасайды. Бұ л кесіндінің бойындағ ы барлық нү ктелердің траекторияла- ры, жылдамдық тары жә не ү деулері бірдей болады.

 

 

                                                                                                                      

 

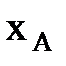
                                           2. 6 сурет                                                          2. 7 сурет

Демек, дененің жазық -параллель қ озғ алысын зерттеу ү шін 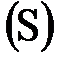 қ имасының қ озғ алысын зерттеген жеткілікті екен.

 қ имасының ө з жазық тығ ындағ ы орны оның бойындағ ы кез келген кесіндісінің орнымен анық талады. 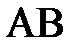 кесіндінің орны кез келген уақ ытта  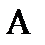нү ктесінің орнымен, яғ ни  нү ктесінің  координаталарымен жә не 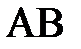 кесіндінің  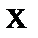ө сімен қ ұ ратын  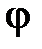бұ рышымен анық талады (1. 7 сурет). Аталғ ан  шамалар уақ ытқ а байланысты ө згеріп отырады. Демек, қ атты дененің жазық -паралель қ озғ алысы ү ш тең деумен беріледі:                                                                            

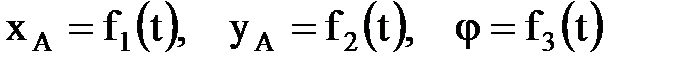                                                          (2. 4. 1)

Бұ л тең деулер дененің жазық -паралель қ озғ алысының заң ы деп аталады.

 нү ктесін полюс деп атайтын боламыз.

Қ атты дененің жазық -паралель қ озғ алысы оның полюспен бірге ілгерілемелі қ озғ алысы мен полюсті айнала қ озғ алысының қ осындысынан тұ ратынын аң ғ ару оң ай. Демек, қ атты дененің жазық -паралель қ озғ алысын екі қ озғ алыстың қ осындысы деп қ арастыруғ а болады: дененің полюспен (А нү ктесі) бірге ілгерілемелі қ озғ алысыжә не полюсті айнала қ озғ алысы. Дене нү ктелері жалпы жағ дайда ә ртү рлі қ озғ алыс жасайтын болғ андық тан, ілгерілемелі қ озғ алыс қ ай нү ктенің полюс ретінде алынғ анына тә уелді, ал айналмалы қ озғ алыс – тә уелсіз болады.

Қ атты дененің жазық -паралель қ озғ алысының негізгі кинематикалық сипаттамаларына полюстің жылдамдығ ы мен ү деуі  жә не дененің полюсті айналғ андағ ы бұ рыштық жылдамдығ ы мен бұ рыштық ү деуі  жатады. Олар дене қ озғ алысының (2. 4. 1) тең деулерінен анық талады. Бұ рыштық жылдамдық пен бұ рыштық ү деу  векторлары қ има жазық тығ ына перпендикуляр бағ ытталғ ан.

2. 4. 2 Жазық -параллель қ озғ алыстағ ы дене нү ктелерінің жылдамдық тары. Жылдамдығ ы белгілі А нү ктесін полюс ретінде алып, жазық қ иманың ө з жазық - тығ ындағ ы қ озғ алысын қ арастырайық (2. 8 сурет). А мен В нү ктелерінің  жә не   радиус-векторларын жү ргізіп, А-дан В-ғ а жү ргізілген векторды 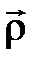 арқ ы- лы белгілейік. Сонда                              .                                      (2. 4. 2)

x

y

O

A

B

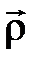
(2. 4. 2) ө рнегінен уақ ыт бойынша бірінші туынды алып,  векторының тек бағ ытының ө згеретінін ескерсек, жазық қ озғ алыстағ ы дене нү ктелерінің жылдам- дық тарын қ осу туралы теореманы алуғ а болады: жазық қ иманың кез келген (В) нү ктесінің жылдамдығ ы полюстің (А) жылдамдығ ы меносы нү ктенің полюсті айналғ анда- ғ ы  жылдамдығ ының геометриялық қ осындысына тең:           

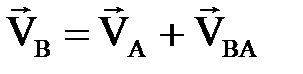                        .                              (2. 4. 3)

         2. 8 сурет              В нү ктесінің полюсті айналғ андағ ы жылдамдығ ының

векторы: 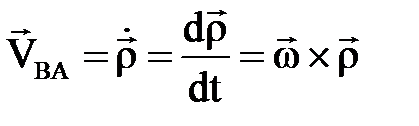                                          ,                       (2. 4. 4)

бұ л вектор АВ-ғ а перпендикуляр w-ның бағ ытымен бағ ытталғ ан, ал сандық мә ні

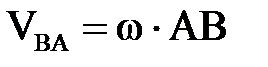                                                                   .                                (2. 4. 5)

2. 4. 3 Жазық қ иманың екі нү ктесі жылдамдық тарының проекциялары туралы теорема.

Теорема. Жазық қ иманың екі нү ктесінің жылдамдық тарының осы нү ктелер арқ ылы ө тетін тү зуге проекциялары ө зара тең (дә лелдемесі дә ріс оқ ығ анда беріледі).

2. 4. 4 Жылдамдық тардың лездік центрі (ЖЛЦ). ЖЛЦ кө мегімен жазық қ има нү ктелерінің жылдамдық тарын анық тау.

⇐ Предыдущая12345Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: