 |
Выполнению контрольных работ
|
|
|
|
Кафедра ОФиФНГП
Сборник задач по физике
И примеры их решения
ЧАСТЬ I
Самара 2015
ББК 22.5
УДК 530.1
УДК 535.(075.8)
Авторы: Т. Н. Голованова, А. М. Штеренберг
Сборник задач по физике и примеры их решения. Часть I /Голованова Т. Н., Штеренберг А. М. – Самара: Самар. гос. техн. ун-т, 2015. – 79 с. ил.
Сборник содержит основные законы и формулы, необходимые для решения задач. Даны примеры решения типовых задач и задачи для самостоятельного решения. Пособие предназначено для студентов-заочников инженерно-технических специальностей вузов. Может быть использовано студентами дневных отделений вузов.
Ил. 32. Табл.2. Библиогр.: 6 назв.
Печатается по решению редакционно-издательского совета СамГТУ
ПРЕДИСЛОВИЕ
Сборник содержит основные законы и формулы, необходимые для решения задач. Даны примеры решения типовых задач и задачи для самостоятельного решения. Числовые данные приведены с учетом точности соответствующих величин и правил действия над приближенными числами.
Учебное пособие предназначено для оказания помощи студентам-заочникам инженерно-технических специальностей вузов при изучении курса общей физики. Может быть полезным для студентов дневных отделений вузов. Пособие составлено в соответствии с действующей программой по курсу физики для технических университетов.
Даны две таблицы вариантов контрольных работ по механике (контрольная работа №1) и молекулярной физике с термодинамикой и электростатикой (контрольная работа №2). Таблицы содержат варианты для специальностей, учебными планами которых, предусмотрено по курсу физики четыре контрольных работы. Кроме того в пособии даны методические указания к решению задач и выполнению контрольных работ, а также, справочные материалы.
|
|
|
программа курса физики
для инженерно-технических специальностей
заочного отделения вуза
Часть I
Механика
Скорость и ускорение материальной точки. Тангенциальное и нормальное ускорения. Угловая скорость и угловое ускорение. Законы Ньютона. Силы в механике. Закон сохранения импульса. Работа и кинетическая энергия. Консервативные силы. Потенциальная энергия, ее связь с работой и консервативной силой. Закон сохранения механической энергии. Момент силы и момент импульса. Закон сохранения момента импульса.
Момент инерции твердого тела. Теорема Штейнера. Уравнение динамики вращения твердого тела. Кинетическая энергия вращающегося твердого тела. Принцип относительности Галилея. Постулаты специальной теории относительности (СТО). Преобразования Лоренца. Следствия из преобразований Лоренца. Релятивистский импульс. Основное уравнение релятивистской динамики. Энергия в СТО. Взаимосвязь массы и энергии.
Виды механических колебаний. Свободные незатухающие колебания. Сложение гармонических колебаний. Свободные затухающие колебания. Логарифмический декремент. Вынужденные колебания. Механические волны. Характеристики волн. Уравнение плоской волны.
Молекулярная физика и термодинамика
Основное уравнение молекулярно-кинетической теории. Средняя энергия молекул. Температура. Уравнение состояния идеального газа. Закон равномерного распределения энергии по степеням свободы. Распределения Максвелла и Больцмана. Скорости молекул. Барометрическая формула. Средняя длина свободного пробега молекул. Явления переноса. Диффузия, теплопроводность и вязкость. Работа газа. Внутренняя энергия и количество теплоты. Первое начало термодинамики. Теплоемкость идеального газа. Адиабатический процесс. Тепловые двигатели. Цикл Карно. Второе начало термодинамики. Энтропия. Закон возрастания энтропии.
|
|
|
ЭЛЕКТРОСТАТИКА
Электрический заряд. Закон Кулона. Напряженность электрического поля. Поток напряженности. Теорема Гаусса для электрического поля в вакууме. Расчет электрических полей с помощью теоремы Гаусса. Потенциал электрического поля. Связь между напряженностью и потенциалом электрического поля. Электрический диполь. Диэлектрики. Поляризация диэлектриков. Свободные и связанные заряды. Электрическое смещение. Расчет электрических полей в диэлектриках. Проводники в электрическом поле. Электроемкость. Конденсаторы. Энергия заряженного проводника и конденсатора. Энергия электрического поля.
Библиографический список
1. Савельев И. В. Курс общей физики: кн. 1: Механика: учеб. пособие / И. В. Савельев. – М.: Астрель, 2004. – 336 с.: ил.
2. Савельев И. В. Курс общей физики: кн. 2: Электричество и магнетизм: учеб. пособие / И.В. Савельев. – М.: Астрель, 2004. – 254 с. ил.
3. Иродов И. Е. Механика. Основные законы: учеб. пособие / И. Е. Иродов. – М.: Лаборатория знаний, 2005. – 309 с.: ил.
4. Иродов И. Е. Физика макросистем. Основные законы: учеб. пособие / И. Е. Иродов. – М.: Лаборатория знаний, 2004. – 207 с.: ил.
5. Детлаф А. А., Яворский Б. М. Курс физики: учеб. пособие / А. А. Детлаф, Б. М. Яворский. – М.: Академия, 2003. – 720 с.: ил.
6. Волькенштейн В. С. Сборник задач по общему курсу физики. Изд. 3-е, исп. и доп. – СПб.: Книжный мир, 2005. – 328 с.
Методические указания к решению задач и
выполнению контрольных работ
Решение задач. Систематическое решение задач обычно проводится по следующей схеме.
1. Сделать анализ условия задачи и записать числовые данные, переведя их при необходимости в одну систему единиц.
2. Определить какие законы и формулы лежат в основе решения данной задачи, дать словесную формулировку этих законов, разъяснить буквенные обозначения формул. Если при решении задачи используется формула, не выражающая какой-либо физический закон, то эту формулу следует вывести.
3. При необходимости выполнить рисунок, поясняющий содержание задачи. Аккуратно выполненный рисунок поможет не только лучше понять условие задачи, но и поможет в выборе необходимого для решения задачи уравнения.
|
|
|
4. Решение задач сопровождается краткими, но исчерпывающими пояснениями, раскрывающими физический смысл формул.
5. Все задачи надо решать в общем виде, т. е. выразить искомую величину в буквенных обозначениях величин, заданных в условии задачи. При таком решении не производятся вычисления промежуточных величин, следовательно, уменьшается вероятность возможных ошибок. Решение в общем виде позволяет так же провести анализ полученного результата.
6. Для проверки правильности полученного решения необходимо в формулу, выражающую искомую величину, подставить единицы величин, заданных в условии задачи и убедиться в том, что полученная единица соответствует искомой величине. Если такого соответствия нет, то задача решена неверно.
7. Выразить числовые значения величин, заданных в условии задачи, в одной системе единиц (преимущественно в СИ) и выписать их для наглядности столбиком. Подставить эти значения в окончательную формулу, выражающую искомую величину, и получить числовой ответ. При этом следует учесть точность числовых данных и на правила действий с приближенными числами. В числовом ответе оставляется столько значащих цифр, сколько их содержится в числовом данном задачи, содержащем наименьшее число этих цифр. Числовой ответ следует записывать в виде произведения десятичной дроби с одной значащей цифрой перед запятой на соответствующую степень десяти. Например, вместо 3250 нужно записать 3,250 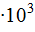 .
.
Выполнение контрольных работ. При выполнении контрольных работ необходимо руководствоваться следующим.
1. Номера задач определяются по таблице вариантов. Номер варианта соответствует последней цифре в шифре студента.
2. Контрольная работа выполняется в обычной школьной тетради, на обложке которой приводятся сведения по следующему образцу:
| Контрольная работа №1 по физике студента электротехнического факультета СамГТУ Андреева А. П. Шифр 201061 Адрес: г. Самара, ул. Тополей 4, кв. 5. |
|
|
|
3. Условия задач записываются полностью без сокращений. Для замечаний преподавателя на страницах тетради оставляются поля.
4. В конце контрольной работы надо указать учебное пособие, используемое при изучении физики (название пособия, автор, год издания). Это надо для того, чтобы рецензент мог указать студенту, что следует изучить для завершения контрольной работы.
5. Высылать одновременно на рецензию нужно не более одной работы.
6. Если контрольная работа не зачтена, то студент обязан представить ее на повторную рецензию, включив в нее те задачи, решения которых оказались неверными.
7. Зачтенная работа предъявляется экзаменатору. Студент должен дать во время экзамена пояснения по существу решения задач, входящих в контрольную работу.
КОНТРОЛЬНАЯ РАБОТА № 1
Механика
Основные формулы
Кинематика
1. Средняя скорость и среднее ускорение материальной точки
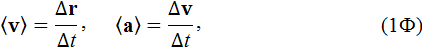
где  ,
, 
 перемещение точки и приращение скорости за время
перемещение точки и приращение скорости за время  ;
; 
 радиус-вектор точки. Используется также средняя скорость, равная отношению пройденного пути s ко времени t, за которое этот путь был пройден
радиус-вектор точки. Используется также средняя скорость, равная отношению пройденного пути s ко времени t, за которое этот путь был пройден
 (2Ф)
(2Ф)
2. Модули скорости и ускорения

где s – путь, пройденный материальной точкой.
3. Проекции скорости и ускорения на координатные оси

 (5Ф)
(5Ф)
4. Модули скорости и ускорения через их проекции на координатные оси

5. Координата точки и проекция скорости на выбранную ось координат при равноускоренном движении

где  ,
, 
 начальная координата и проекция начальной скорости.
начальная координата и проекция начальной скорости.
6. Тангенциальное и нормальное ускорения при криволинейном движении

где  – радиус кривизны траектории в данной точке, или радиус окружности.
– радиус кривизны траектории в данной точке, или радиус окружности.
7. Модули угловой скорости и углового ускорения точки, движущейся по окружности,

где 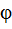
 угол поворота радиус-вектора точки.
угол поворота радиус-вектора точки.
8. Связь между модулями линейных и угловых величин, характеризующих движение точки по окружности,
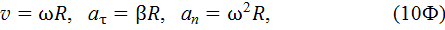
где 
 линейная скорость; R – радиус окружности.
линейная скорость; R – радиус окружности.
9. Полное ускорение точки, движущейся по окружности,

Динамика
10. Второй закон Ньютона
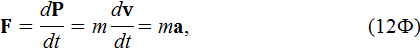
где 
 равнодействующая сила, действующая на тело (материальную точку) массой m;
равнодействующая сила, действующая на тело (материальную точку) массой m; 
 импульс тела;
импульс тела; 
 его скорость; а – ускорение тела.
его скорость; а – ускорение тела.
11. Третий закон Ньютона

Силы, с которыми взаимодействуют два тела, равны по модулю и противоположны по направлению, имеют одинаковую природу и приложены к разным телам.
12. Силы в механике:
а) гравитационная сила (закон всемирного тяготения)

где G – гравитационная постоянная (находится из таблицы); 
 массы взаимодействующих тел; R – расстояние между телами (тела рассматриваются как материальные точки или однородные шары);
массы взаимодействующих тел; R – расстояние между телами (тела рассматриваются как материальные точки или однородные шары);
|
|
|
б) сила упругости (закон Гука)

где 
 проекция силы упругости на ось Х;
проекция силы упругости на ось Х; 
 коэффициент упругости (жесткость в случае пружины);
коэффициент упругости (жесткость в случае пружины); 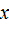
 проекция перемещения конца пружины или стержня при деформации. Знак «минус» означает, что проекции силы упругости и перемещения конца пружины (стержня) имеют противоположные знаки;
проекция перемещения конца пружины или стержня при деформации. Знак «минус» означает, что проекции силы упругости и перемещения конца пружины (стержня) имеют противоположные знаки;
в) сила трения скольжения

где 
 коэффициент трения скольжения, зависит от природы и состояния трущихся поверхностей;
коэффициент трения скольжения, зависит от природы и состояния трущихся поверхностей; 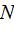
 сила нормального давления.
сила нормального давления.
Законы сохранения
13. Закон сохранения импульса

Импульс замкнутой системы тел (или частиц) остается постоянным, т. е. не меняется со временем. Для двух тел (i = 2)
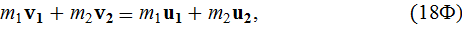
где 
 скорости тел до взаимодействия;
скорости тел до взаимодействия;  ,
, 
 скорости тел после взаимодействия.
скорости тел после взаимодействия.
14. Работа, совершаемая силой F при перемещении частицы из точки 1 в точку 2,
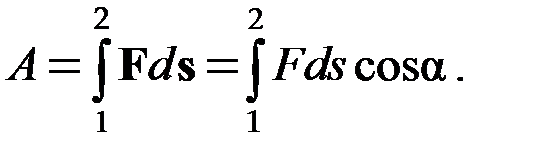 (19Ф)
(19Ф)
где 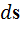
 элементарное перемещение частицы;
элементарное перемещение частицы; 
 угол между перемещением
угол между перемещением 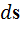 и силой
и силой  .
.
15. Кинетическая энергия частицы

16. Связь кинетической энергии с работой
А = Δ Е к = Е к2 – Е к1, (21Ф)
где 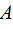
 работа всех сил, действующих на частицу;
работа всех сил, действующих на частицу; 
 приращение кинетической энергии частицы; Е к1, Е к2 – кинетическая энергия частицы в моменты времени
приращение кинетической энергии частицы; Е к1, Е к2 – кинетическая энергия частицы в моменты времени  и
и  . Выражение (21Ф) обобщается на механическую систему: работа всех сил (внутренних и внешних) равна приращению кинетической энергии системы.
. Выражение (21Ф) обобщается на механическую систему: работа всех сил (внутренних и внешних) равна приращению кинетической энергии системы.
17. Потенциальная энергия:
а) упругодеформированной пружины

б) тела, находящегося в однородном поле силы тяжести
Е п = mgh, (23Ф)
где h  высота тела над уровнем, принятым за нулевой. Формула справедлива при h
высота тела над уровнем, принятым за нулевой. Формула справедлива при h  R, где R
R, где R  радиус Земли.
радиус Земли.
18. Связь потенциальной энергии с работой консервативных сил

где 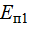 ,
, 
 потенциальная энергия в точках 1 и 2 консервативного поля (например, поля тяжести Земли). Для механической системы под
потенциальная энергия в точках 1 и 2 консервативного поля (например, поля тяжести Земли). Для механической системы под 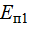 ,
, 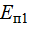 следует понимать потенциальную энергию системы в двух ее положениях или конфигурациях (начальном
следует понимать потенциальную энергию системы в двух ее положениях или конфигурациях (начальном 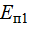 и конечном
и конечном 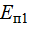 ).
).
19. Закон сохранения энергии
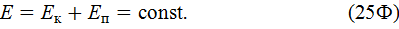
Полная механическая энергия E системы, находящейся под действием консервативных сил, сохраняется с течением времени.
Динамика твердого тела
20. Моменты инерции тел массой m относительно оси, проходящей через их центр масс:
а) обруча (и тонкостенного цилиндра) радиуса R относительно оси, перпендикулярной плоскости обруча (или оси цилиндра),
 ; (26Ф)
; (26Ф)
б) диска (и сплошного цилиндра) радиуса R относительно оси, перпендикулярной плоскости диска (или оси цилиндра),

в) стержня длиной l относительно оси, нормальной стержню,

21. Теорема Штейнера

Момент инерции тела I относительно произвольной оси равен сумме момента инерции  относительно оси, параллельной данной и проходящей через центр масс тела, и произведению массы тела m на квадрат расстояния a между осями.
относительно оси, параллельной данной и проходящей через центр масс тела, и произведению массы тела m на квадрат расстояния a между осями.
22. Момент импульса тела относительно неподвижной оси вращения Z

где 
 проекция угловой скорости тела на ось Z.
проекция угловой скорости тела на ось Z.
23. Закон сохранения момента импульса тела и системы тел

Для системы тел: I  суммарный момент инерции системы;
суммарный момент инерции системы; 
 проекция угловой скорости на ось Z.
проекция угловой скорости на ось Z.
24. Уравнение динамики твердого тела, вращающегося вокруг неподвижной оси Z,

где 
 проекция углового ускорения на ось Z;
проекция углового ускорения на ось Z; 
 результирующий момент внешних сил относительно оси Z.
результирующий момент внешних сил относительно оси Z.
25. Кинетическая энергия твердого тела, вращающегося вокруг неподвижной оси,

26. Кинетическая энергия при плоском движении твердого тела

где 
 момент инерции тела относительно оси, проходящей через его центр масс;
момент инерции тела относительно оси, проходящей через его центр масс;  скорость центра масс.
скорость центра масс.
Механические колебания
27. Дифференциальное уравнение свободных незатухающих гармонических колебаний частицы

где x  смещение частицы от положения равновесия;
смещение частицы от положения равновесия; 
 циклическая частота свободных колебаний.
циклическая частота свободных колебаний.
28. Период колебаний физического маятника

где I  момент инерции маятника относительно неподвижной горизонтальной оси (оси качания); m
момент инерции маятника относительно неподвижной горизонтальной оси (оси качания); m  масса маятника; g
масса маятника; g  ускорение свободного падения; l
ускорение свободного падения; l  расстояние от точки подвеса до центра масс маятника.
расстояние от точки подвеса до центра масс маятника.
29. Период колебаний тела массой m под действием квазиупругой силы

где k  коэффициент упругости (жесткость пружины).
коэффициент упругости (жесткость пружины).
30. Приведенная длина физического маятника, равная длине математического маятника, имеющего такой же период, что и физический
 (38Ф)
(38Ф)
31. Кинематическое уравнение гармонических колебаний
 (39Ф)
(39Ф)
где 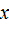 – смещение точки, равное ее координате в момент времени t; А – амплитуда колебаний;
– смещение точки, равное ее координате в момент времени t; А – амплитуда колебаний; 
 циклическая частота;
циклическая частота; 
 фаза колебаний; φ0 – начальная фаза.
фаза колебаний; φ0 – начальная фаза.
32. Амплитуда A и начальная фаза 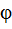 результирующего колебания
результирующего колебания
при сложении двух колебаний одного направления и одинаковой частоты:

где 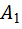 ,
, 
 амплитуды складываемых колебаний;
амплитуды складываемых колебаний;  ,
, 
 начальные фазы колебаний;
начальные фазы колебаний;

|
|
|


