 |
Специальная теория относительности
|
|
|
|
33. Линейные размеры тела (длина стержня), движущегося относительно инерциальной системы отсчета (ИСО) со скоростью 
,
где l 0 
собственные размеры тела, или собственная длина стержня; c скорость света в вакууме. Из (42Ф) видно, что линейные размеры тела уменьшаются в направлении его движения.
34. Собственный интервал времени, измеренный по часам, движущимся вместе с телом,
где 
интервал времени, измеренный по часам в ИСО, относительно которой тело движется со скоростью . Из (43Ф) видно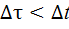 
. Это означает, что движущиеся часы идут медленнее, чем неподвижные, т. е. существует эффект замедления хода движущихся часов.
35. Релятивистское выражение для импульса тела, движущегося со скоростью v относительно ИСО,
где m масса тела, постоянная во всех ИСО, т. е. не зависящая от скорости тела. При 
релятивистский импульс переходит в классическое выражение 
.
36. Энергия покоя тела
37. Кинетическая энергия тела
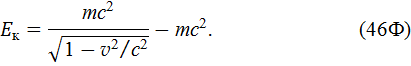
38. Полная энергия тела
39. Связь между импульсом и кинетической энергией тела
(48Ф)
Из этого соотношения при E к << mc 2 получается формула 
, которая используется в механике Ньютона.
Примеры решения задач
Пример 1. Автомобиль проехал расстояние между двумя городами за некоторое время. Половину этого времени он шел со скоростью 
В оставшееся время половину пути он шел со скоростью 
, а вторую половину со скоростью 
. Найти среднюю скорость автомобиля на всем пути между городами.
|
|
|
 .
|
  
|
| A |
| B |
|
|
|
|
|
|
|
|
| Рис. 1 |
Изобразим траекторию прямолинейного движения автомобиля и отложим на ней пути , , , проходимые автомобилем за время , , соответственно со скоростью , , (см. рис. 1). Средняя скорость автомобиля на всем пути s находится по формуле (2Ф)
|
|
|
где
, 
, 
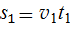. (2)
По условию задачи 
, или с учетом (2)
. (3)
Из условия задачи видно так же
. (4)
Тогда (1) запишется
Пройденные пути s 1 и s 2 берутся из уравнений (2). С учетом (4) путь s 2 = v 2 (t 1 – t 3), где t 3 = s 3/ v 3 (см. (2)). Учитывая s 3 = s 2, получим:
s 2 = v 2 (t 1 – s 2/ v 3).
Откуда
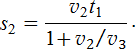
Учитывая это выражение и путь 
из уравнений (2), находим из (5) искомую среднюю скорость:
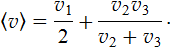
Пример 2. Жонглер бросил вертикально вверх мячик. Когда мячик достиг верхней точки своего подъема 
= 4,9 м, жонглер бросил вверх второй мячик с той же начальной скоростью 
. На какой высоте встретятся тела?
| =4,9 м.
|
|
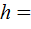
Решение
Воспользуемся формулой координаты при равноускоренном движении (см. (7Ф), где x = y). Время отсчитывается с момента броска второго тела. В этот момент начальная координата первого тела y 0 = h м (рис. 2). Проекция ускорения свободного падения на ось Y будет отрицательной, т. к. ускорение g направлено против оси Y. С учетом этого координаты первого и второго тел запишутся следующим образом:
|
|
|
| С |
| Y |
|
| Рис. 2 |
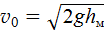. Подставляя это выражение в (2), получим:
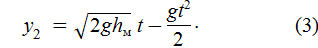
В момент встречи 
, откуда, учитывая (1) и (3), найдем время, через которое тела встретятся
. (4)
При 
координата 
. Тогда из (1) найдем
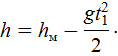
Подставляя сюда (4), получим искомую высоту:
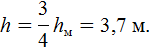
Тот же результат получится, если использовать координату (3).
Пример 3. Из одной точки одновременно бросили два тела под углами 
и 
к горизонту с начальными скоростями 
и 
. Траектории тел лежат в одной плоскости (рис. 3). На каком расстоянии l друг от друга будут находиться тела через время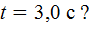 
 .
|
| l
|
Решение
|
|
|
|
| A |
|
| С |
| B |
|
|
|
|
|
|
| 2 |
| Рис. 3 |
|
|
В отсутствии сопротивления воздуха движение тел является свободным падением, происходящим по параболе. На рис. 3 показаны примерные траектории движения тел и их положение через заданное время (точки А и В). Искомое расстояние между телами l = ú АВ ú = 
, или через координаты тел (точек)
|
|
|
. (1)
Используя формулу координаты для заданных движений (см. (7Ф)), найдем:
, 
,
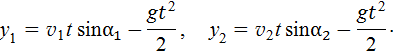
Подставляя эти координаты в (1) и, используя формулу из тригонометрии
(
) = 
+ 
,
получим:
|
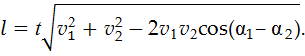(2)
|
|
| Рис. 4 |
|
|
Учитывая числовые данные, найдем: l = 30 м. Интересно отметить, что квадратный корень в выражении (2) представляет собой модуль относительной скорости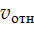 
тел (см. рис. 4). В этом легко убедиться, применяя теорему косинусов к треугольнику скоростей
(3)
Видно, что 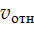не зависит от времени, т. е. при движении скорость одного тела относительно другого по модулю остается постоянной. Тогда, учитывая (3), расстояние между телами можно выразить через относительную скорость: 
.
Пример 4. Тело вращается вокруг неподвижной оси по закону φ = A + Bt + C 
, где A = 10 рад, B = 20 рад/с, C = 
2,0 рад/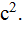 
Найти полное ускорение точки, находящейся на расстоянии R = 0,10 м от оси вращения, для момента времени t = 4,0 с.
Решение
 = A + Bt + C 
A = 10 рад,
B = 20 рад/с,
C = 2,0 рад/  ,
R = 0,10 м,
t = 4,0 с.
|
| а
|
| Рис. 5 |
|
|
|
Полное ускорение точки, движущейся по окружности, равно геометрической сумме тангенциального ускорения , направленного по касательной к траектории, и нормального ускорения , направленного к центру окружности (рис. 5)
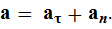
Так как векторы 
и 
взаимно перпендикулярны, то модуль ускорения (см. (11Ф))
Модули тангенциального и нормального ускорений точки вращающегося тела выражаются формулами
, 
, (2)
где β, ω 
модули углового ускорения и угловой скорости. Подставляя выражения (2) в формулу (1), получим:
(3)
Угловую скорость 
найдем, взяв первую производную угла поворота по времени (см. условие задачи). Тогда в момент времени t = 4,0 с модуль угловой скорости
= d / dt = B + 2 Ct = 4,0 рад/с.
Угловое ускорение найдем, взяв первую производную от угловой скорости по времени,
= d / dt = 2 C = 4,0 рад/ .
Подставляя числовые значения , и R в формулу (3), найдем: a =1,6 м/ .
Пример 5. На тело массой m, лежащее на гладкой горизонтальной плоскости, в момент времени t 0 = 0 начала действовать сила, зависящая от времени, F = kt, где k – постоянная величина. Направление этой силы все время составляет угол 
с горизонтом (см. рис. 6). Найти: а) скорость тела в момент отрыва от плоскости; б) путь, пройденный телом к этому моменту.
|
|
|
m,
.
|
|
Решение
|
|
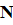
| X |
| Y |
| Рис. 6 |
|
|
|
На тело действуют: сила F; сила тяжести m g и сила реакции N (рис. 6). Сила трения отсутствует, т. к. поверхность гладкая. Под действием этих сил тело движется с ускорением а = d v / dt вдоль оси X. Применим второй закон Ньютона (см. (12Ф))
или в проекциях на оси X, Y
Учли условие задачи 
. Из уравнения (2) имеем
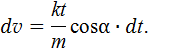
После интегрирования получим скорость тела
В момент отрыва от плоскости N = 0 и из уравнения (3) находим время отрыва
Подставляя это время в (4), найдем скорость тела в момент отрыва от плоскости:
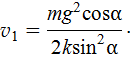
Путь, пройденный телом 
(см. (3Ф), первая формула). Учитывая (4), запишем:
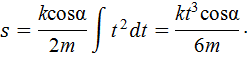
Подставляя сюда время отрыва (5), найдем путь, пройденный телом к моменту отрыва от плоскости:
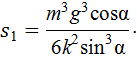
Пример 6. Частица массой m в момент t = 0 начинает двигаться под действием силы 
, где 
и 
постоянные величины. Найти путь, пройденный частицей, в зависимости от времени t.
 .
|
|
Решение
Используем второй закон Ньютона (12Ф)
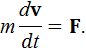
Учитывая условие задачи, запишем:
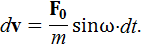
После интегрирования в пределах от 0 до t получим
Путь, пройденный частицей за время t (см. (3Ф)),
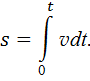
Подставим в эту формулу выражение (1) в скалярном виде
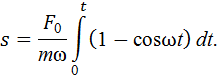
Выполняя интегрирование в указанных пределах, найдем путь
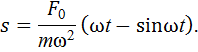
Пример 7. Искусственный спутник Земли имеет круговую орбиту, удаленную от поверхности Земли на расстояние h = 260 км. Определить период обращения спутника Т относительно центра Земли. Радиус Земли R = 6,4 
км.
Решение
R = 6,4   .
|
|
На искусственный спутник Земли (ИЗС) действует только сила притяжения (тяготения) к Земле (силой тяготения со стороны Луны и Солнца пренебрегаем), которая сообщает спутнику нормальное (центростремительное) ускорение (см. (8Ф), вторая формула)
где скорость спутника относительно центра Земли; 
радиус круговой орбиты спутника. Применим второй закон Ньютона для ИЗС
, (2)
где m масса спутника; 
сила тяготения, определяется законом всемирного тяготения (14Ф). Для данной задачи
|
|
|
где 
гравитационная постоянная; 
масса Земли. Учитывая (1) и (3), из второго закона Ньютона (2) найдем: 
(4)
Применяя второй закон Ньютона (12Ф) к свободно падающему телу, находящемуся у поверхности Земли (h = 0), получим с учетом (3):
Поделив (4) на (5), найдем скорость ИЗС
Полагая движение спутника по круговой орбите равномерным, запишем (см. (2Ф)):
Из (6) и (7) найдем период обращения спутника
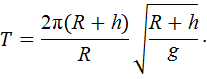
Если положить ускорение свободного падения g =9,8 м/ 
, то получим T = 90 мин.
Пример 8. Лодка массой m стоит неподвижно на поверхности озера. На корме и на носу лодки на расстоянии l друг от друга сидят два рыбака массам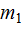и 
и 
. Для улучшения клева рыбаки меняются местами. В какую сторону и на какое расстояние переместится лодка?
| m,
,
,
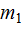l.
|
|
Решение
Система «лодка 
рыбаки» не является замкнутой, т. к. на нее действуют внешние силы: сила тяжести и сила Архимеда. Эти силы уравновешивают друг друга, а сила трения лодки о воду пренебрежимо мала по сравнению с силами взаимодействия рыбаков с лодкой (внутренние силы). Поэтому можно применить закон сохранения импульса (17Ф). Импульс системы до начала движения рыбаков равен нулю. Следовательно, после начала движения суммарный импульс также равен нулю
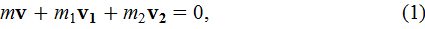
| Рис. 7 |
|
|
| l |
|
|
|
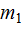
| X |
|
|
|
|
|
|
|
, 
, 
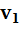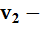скорости лодки и рыбаков относительно воды. Допустим, 
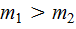и лодка движется в направлении перемещения рыбака с меньшей массой m 2 (см. рис. 7, где цифрами 1 и 2 обозначены положения рыбаков после перемещения лодки). Тогда равенство (1) в проекциях на ось X запишется
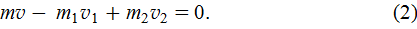
Из рис. 7 видно
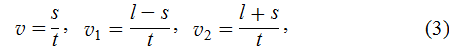
где s модуль перемещения лодки; t время движения лодки и рыбаков, которое одинаково для всех тел. Подставляя (3) в (2), найдем:
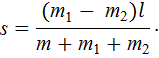
При условии 
и для выбранного направления оси X имеем
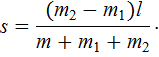
Полученные решения можно объединить в одну формулу, если ввести проекцию перемещения лодки на ось Х
При 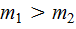проекция 
0 и лодка перемещается влево При , 
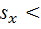0 и лодка перемещается в противоположную сторону.
Пример 9. Снаряд массой m = 10,0 кг летит горизонтально со скоростью = 200 м/с и разрывается на две части (осколки). Одна часть массой 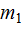= 3,00 кг полетела вперед под углом 
к горизонту со скоростью = 400 м/с. С какой скоростью и в каком направлении полетела вторая часть снаряда?
Решение
| m = 10,0 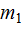кг,
= 3,00 кг,
= 200 м/с,
= 400 м/с,
.
|
β =?
|
| X |
| Рис. 8 |
|
|
| Y |
m 
|
|
|
|
|
|
|
Система «снаряд осколки» не является замкнутой, т. к. на тела
системы действует сила тяжести. Если рассматривать суммарный импульс осколков сразу после разрыва, то он будет равен импульсу снаряда непосредственно до разрыва. Это следует из того, что за время разрыва снаряда импульсы осколков практически не изменяются. Таким образом, к нашей системе можно применить закон сохранения импульса (см. (18Ф))
|
|
|
Здесь 
импульс снаряда до разрыва; 
, 
импульсы осколков. Импульсы осколков и снаряда, показаны на рис. 8 в соответствии с законом сохранения импульса системы «снаряд осколки». Спроектируем (1) на оси координат (см. рис. 8)
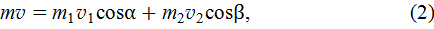
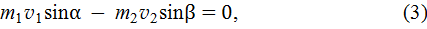
где искомый угол, под которым полетела к горизонту вторая часть снаряда, находится из уравнений (2) и (3)
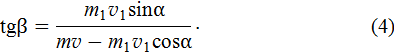
Скорость второй части находим из уравнения (3)
Подставляя числовые данные задачи в (4) найдем: 
. Тогда из формулы (5) найдем = 250 м/с.
Задачу можно решить также с использованием теоремы косинусов. Из рис. 8 видно
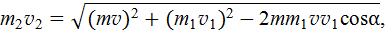
откуда находим . Угол находим также из теоремы косинусов
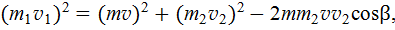
откуда
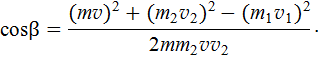
При этом закон сохранения импульса (1) используется при построении треугольников, к которым применялась теорема косинусов.
Пример 10. Тело массой соскальзывает без трения по наклонному желобу, переходящему в окружность. Тело соскальзывает с наименьшей высоты, необходимой для совершения полного оборота. Найти силу давления на желоб в точке А, радиус-вектор которой составляет угол с вертикалью. Из полученного решения определить силу давления тела на желоб в верхней В и нижней С точках петли.
|
.
|
|
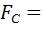
Решение
Искомая сила давления 
по третьему закону Ньютона равна по модулю силе нормальной реакции N (см. рис. 9)
Величина N находится из второго закона Ньютона (12Ф), записанного в проекциях на ось X для тела, находящегося в точке А (см. рис. 9),
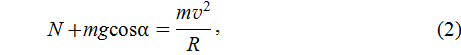
где скорость тела в точке А; R радиус окружности, по которой движется тело; v 2/ R – нормальное ускорение тела в точке А.
| D |
| X |
| Рис. 9 |
|
|
| С |
| В |
| R |
| А |
|
| h |
| О |
| N |
|
|
|
|
|
|
|
| v |
В системе «тело Земля» отсутствуют силы трения и сопротивления, следовательно, можно использовать закон сохранения энергии (25Ф). В точке D тело обладает потенциальной энергией (23Ф)
= mg , (3)
где наименьшая высота, необходимая для совершения полного оборота. В точке А полная энергия тела состоит из потенциальной (см. (23Ф)) и кинетической (20Ф) энергии
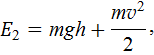
где 
(см. рис. 9). Тогда
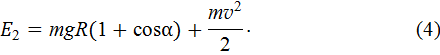
По закону сохранения энергии 
, или, учитывая (3) и (4), получим:
Тело скатывается с наименьшей высоты , необходимой для совершения полного оборота. Следовательно, в наивысшей точке траектории (точка В, рис. 9) на тело действует только сила тяжести (состояние невесомости). Применим второй закон Ньютона в этойточке
и закон сохранения энергии для положений тела в точках D и В
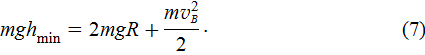
Из (6) и (7) имеем
Подставив (8) в (5), получим:
Из уравнений (2) и (9) с учетом (1) найдем искомое давление
Угол отсчитывается от вертикали по часовой стрелке. Следовательно, в верхней точке петли (точка В) =0 и 0. (см. (10)). Этот результат мы ранее использовали при нахождении (6) и получили его из физических соображений (тело скатывается с минимальной высоты , необходимой для совершения полного оборота). Для нижней точки петли (точка С) угол = 
, тогда из (10) следует
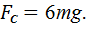
Пример 11. Тело массой M лежит на вершине гладкой полусферы радиуса R. В тело попадает пуля массой m, летящая горизонтально со скоростью , и застревает в нем. Пренебрегая смещением тела во время удара, найти высоту h, на которой оно оторвется от поверхности полусферы. Высота отсчитывается от основания полусферы. При какой скорости пули 
тело сразу оторвется от полусферы?
| M,
m,
R,
.
|
 =?
|
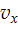Решение
Полусфера гладкая, поэтому в системе «тело Земля» сила трения отсутствует. Сила сопротивления воздуха также не учитывается. Следовательно, можно использовать закон сохранения энергии (25Ф). Полная энергия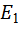 
тела вместе с пулей сразу после удара равна энергии 
тела с пулей в момент отрыва от полусферы. Энергия 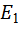находится в точке 1 на вершине полусферы (см. рис. 10)
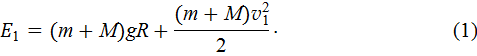
| Рис.10 |
| h |
| X |
|
|
| R |
| О |
|
| 1 |
| 2 |
|
|
|
| М |
|
|
|
