Задачи для самостоятельного решения

101. Теплоход идет по реке от одного пункта до другого со скоростью 12 км/ч относительно берега, а обратно со скоростью 20 км/ч. Найти среднюю скорость теплохода относительно берега и скорость течения реки. Скорость теплохода относительно воды считать постоянной.

102. Автомобиль прошел половину пути со скоростью . На остальной части пути он половину времени двигался со скоростью , а оставшийся участок – со скоростью . Найти среднюю скорость за все время движения автомобиля.

103. Вертикально вверх с интервалом времени τ брошены два шарика с одинаковой скоростью из одной и той же точки. Через какое время после броска второго шарика они столкнутся?

104. Под каким углом к горизонту необходимо бросить тело, чтобы: а) центр кривизны вершины его траектории находился на земной поверхности; б) радиус кривизны начала его траектории был в η = 8,0 раза больше, чем в вершине?

105. Частица движется в плоскости ХY по закону , , где и – положительные постоянные. Найти: а) уравнение траектории частицы ; б) скорость и ускорение a в зависимости от времени .

106. Два тела бросили одновременно из одной точки: одно вертикально вверх, другое под углом к горизонту. Начальная скорость каждого тела 25 м/с. Найти расстояние между телами через время t = 1,7 с.

107. Тело бросили под углом к горизонту со скоростью м/с. Найти нормальное a_n и тангенциальное ускорения через время t = 5 c после начала движения тела?

108. Две частицы движутся с ускорением свободного падения g в однородном поле тяжести. В начальный момент времени частицы на­ходились в одной точке и имели скорости 3,0 м/с и 4,0 м/с, направленные горизонтально и в противоположные стороны. Найти расстояние между частицами в момент времени, когда векторы их скоростей окажутся взаимно перпендикулярными.

109. Твердое тело начинает вращаться вокруг неподвижной оси с угловым ускорением , где . Через, сколько времени после начала вращения полное ускорение произвольной точки тела будет составлять угол с ее скоростью?

110. Колесо вращается вокруг неподвижной оси, при этом угол 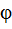его поворота зависит от времени как 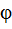= , где = 0,20 рад/ . Найти полное ускорение a точки на ободе колеса в момент t = 2,5 с, если скорость точки в этот момент = 0,65 м/с.

111. На частицу действует сила , где i, j орты осей Х, У. Найти импульс частицы в момент времени = 2,0 с.

112. Аэростат массой m = 250 кг начал опускаться с ускорением . Найти массу балласта, который надо сбросить за борт, чтобы аэростат получил такое же ускорение, но направленное вертикально вверх. Сопротивление воздуха не учитывать.

Рис. 13

113. В установке, показанной на рис. 13, массы тел равны , массы блока и нитей пренебрежимо малы. Трение в блоке не учитывать. Найти ускорение 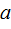, с которым опускается тело массой , и силу натяжения нити, связывающей тела массами m ₁ и m ₂, если коэффициент трения между этими телами и горизонтальной поверхностью равен .

114. Небольшое тело пустили снизу вверх по наклонной плоскости, составляющей угол с горизонтом. Найти коэффициент трения, если время подъема тела оказалось в 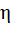= 2,0 раза меньше времени спуска.

115. Автомобиль едет по шоссе со скоростью v = 72 км/ч. Коэффициент трения между колесами автомобиля и дорогой μ = 0,30. За какое минимальное время автомобиль сможет развернуться, не снижая скорости?

116. Велосипедист едет по круговой горизонтальной площадке ра-диуса R. Коэффициент трения где μ₀ – постоянная величина; r – расстояние от велосипедиста до центра O площадки. Найти максимальный радиус окружности r _max с центром в точке О, по которой велосипедист может ехать с максимальной скоростью. Какова эта скорость?

117. На покоившуюся частицу массой m в момент t = 0 начала действовать сила, зависящая от времени по закону F = b t ( t), где b постоянная величина, время действия силы. Найти: а) импульс частицы после окончания действия силы; б) путь, пройденный частицей за время действия силы.

118. К бруску массой m, лежащему на гладкой горизонтальной плоскости, приложили постоянную по модулю силу F = mg /3. В процессе его прямолинейного движения угол между направлением этой силы и плоскостью изменяется по закону = ks, где k постоянная величина; s пройденный бруском путь (из начального положения). Найти скорость бруска как функцию угла .

119. Частица массой m в момент времени t = 0 начинает двигаться под действием силы F = sin t, где , постоянные величины. Найти путь, пройденный частицей в зависимости от времени t.

120. В момент времени t = 0 частица массой m начинает двигаться под действием силы F = F₀ cosω t, где F₀ и ω – постоянные величины. Сколько времени тело будет двигаться до первой остановки? Какой путь она пройдет за это время?

121. Найти отношение кинетической энергии спутника планеты к его потенциальной энергии. Спутник движется по круговой орбите.

122. Насколько переместиться относительно воды лодка длиной l = 3,5 м и массой = 200 кг, если человек массой = 80 кг перешел с кормы на нос лодки?

123. Тело массой 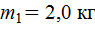упруго сталкивается с покоящимся телом, при этом его скорость уменьшилась в n = 2 раза и изменилась по направлению на угол α = . Найти массу m ₂ второго тела.

124. Граната, летит горизонтально и разрывается на два осколка. Скорость одного осколка = 30 м/с и направлена под углом 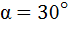к горизонту. Скорость другого осколка = 60 м/с и направлена вертикально вниз. Найти скорость гранаты до разрыва. Во сколько раз масса одного осколка больше другого?

125. Человек массой M стоит на льду и толкает в горизонтальном направлении санки массой m, сообщая им скорость , при этом он откатывается назад. Какую работу совершает при этом человек?

126. Спортсмен массой , стоя на коньках, бросает тело массой под углом к горизонту со скоростью v ₂ = 5,0 м/с. На какое расстояние откатится спортсмен после броска, если коэффициент трения коньков о лед . Перемещение спортсмена во время броска не учитывать.

127. Какую работу надо совершить, чтобы тело массой m = 10 кг втащить по наклонной плоскости высотой h = 1,5 м и основанием a = 2,5 м. Коэффициент трения .

128. Доска массой M равномерно движется по гладкой горизонтальной поверхности со скоростью . Сверху на доску осторожно кладут кирпич массой . Какое расстояние пройдет кирпич по доске за время его проскальзывания до остановки? Коэффициент трения между кирпичем и доской равен .

129. Небольшое тело соскальзывает с высоты h = 8,0 м по наклонной плоскости, плавно переходящей в «мертвую петлю» радиусом R = 4,0 м. На какой высоте, считая от нижней точки петли, тело оторвется от ее поверхности?

130. На тележку массой M, движущуюся по горизонтальной прямой с постоянной скоростью , падает с высоты h кирпич массой m. Кирпич остается на тележке. Найти количество теплоты Q, выделившейся при этом.

131. Свинцовая пуля массой m = 10 г летит горизонтально со скоростью v = 100 м/с и попадает в деревянный брусок массой М = 1,0 кг, подвешенный на длинной нити. Насколько увеличится температура пули, если η = 70 % выделенной теплоты идет на ее нагревание?

132. На сплошной однородный цилиндр радиусом R = 10 см и массой 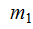= 9,0 кг плотно намотана нить, к концу которой привязан груз массой = 2,0 кг (рис. 14). Найти угловое ускорение цилиндра.

133. Однородный сплошной цилиндр массой m = 8,0 кг и радиусом R = 1,3 см (рис. 15) в момент времени t = 0 начинает опускаться под действием силы тяжести. Найти угловое ускорение β цилиндра.

R

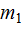
m

R

Рис. 14

Рис. 15

134. В установке (рис. 16) известны масса сплошного однородного цилиндра m, его радиус R и массы тел 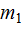и . Скольжение нити по поверхности цилиндра и трение в его оси не учитывать. Найти угловое ускорение β цилиндра.

 

R

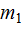
Рис. 17

Рис. 16

Рис. 17

Рис. 16

 

135. Сплошной однородный цилиндр массой m вращается под действием сил натяжения нити, к концам которой подвешены грузы массам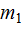и и (рис. 16). Найти отношение сил натяжения вертикальных участков 1 и 2 нити в процессе движения. Убедится, что при m → 0 = .

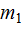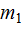136. В системе, показанной на рис. 17, известны: массы тел и коэффициент трения между телом массой и горизонтальной плоскостью, а также масса блока m, который можно считать однородным сплошным диском. Скольжение нити по блоку отсутствует. В момент t = 0 тело массой начинает опускаться. Пренебрегая массой нити и трением в оси блока, найти ускорение a тела массой .

 

R

Рис. 19

137. По горизонтальной плоскости катится диск (рис. 18) и, предоставленный самому себе, остановился, пройдя расстояние s = 16 м. Начальная скорость диска, v =8 м/с. Найти коэффициент трения.

138. Однородный цилиндр радиусом R раскрутили вокруг его оси до угловой скорости и поместили в угол (рис. 19), коэффициент трения между стенками угла и цилиндром равен . Сколько оборотов n сделает цилиндр до остановки?

139.Тонкий однородный стержень длиной l из вертикального положения падает на горизонтальную поверхность. Найти линейные скорости крайней и средней точек стержня в момент времени, когда стержень займет горизонтальное положение.

140. Сколько времени будет скатываться без скольжения обруч с наклонной плоскости длиной l = 2 м и высотой h = 10 см?

141. Человек массой 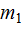стоит на краю горизонтального однородного диска массой и радиусом R. Диск может свободно вращаться вокруг вертикальной оси, проходящей через его центр. В некоторый момент человек начал двигаться по краю диска, совершил перемещение на угол относительно диска и остановился. Пренебрегая размерами человека, найти угол 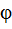, на который повернется диск к моменту остановки человека.

142. Однородный шар скатывается без скольжения по наклонной плоскости, составляющей угол α с горизонтом. Найти ускорение центра шара и коэффициент трения, при котором скольжения не будет.

143. Математический маятник длиной l = 1,5 м совершает гармонические колебания с амплитудой А = 10 см. Найти максимальную скорость грузика маятника.

144. При перемещении математического маятника с Земли на другую планету период его колебаний увеличился в n ₁ = 6 раз. Во сколько раз масса Земли больше массы планеты, если радиус Земли в n ₂ = 2 раза больше радиуса планеты?

145. Математический маятник, состоящий из шарика массой m = 260 г и нити длиной l = 2,4 м, совершает гармонические колебания с амплитудой А = 10 см. Найти скорость шарика при прохождении положения равновесия и максимальное значение силы, под действием которой совершаются колебания.

146. Математический маятник длиной l ₀ = 40 см и тонкий однородный стержень длиной l = 60 см совершают синхронно гармонические колебания вокруг горизонтальной оси. Найти расстояние от центра стержня до этой оси.

147. Обруч диаметром D = 56 см висит на гвозде и совершает гармонические колебания под действием силы тяжести. Найти период колебаний обруча, принимая его за физический маятник.

148. На стержне длиной l ₀ = 60 см укреплены два одинаковых грузика: один в середине стержня, другой – на конце. Стержень с грузиками колеблется около горизонтальной оси, проходящей через его свободный конец. Найти приведенную длину и период гармонических колебаний данного маятника. Массой стержня пренебречь.

149. Частица совершает гармонические колебания с начальной фазой α = 0. При смещении частицы от положения равновесия на х ₁ = 4 см ее скорость = 6 см/с, а при смещении на х ₂ = 3 см скорость = 8 см/с. Определить циклическую частоту колебаний ω₀.

150. Пружинный маятник вывели из положения равновесия и отпустили. Через какое время (в долях периода) кинетическая энергия колеблющегося тела будет равна потенциальной энергии пружины?. Массу пружины не учитывать.

151. Шарик, подвешенный на пружине, отвели из положения рав-новесия вертикально вниз на расстояние х = 4,0 см и сообщили ему скорость = 1,0 м/с, после чего шарик стал совершать гармонические колебания с частотой ω₀ = 25 рад/с. Найти амплитуду колебаний.

152. Стержень движется в продольном направлении с постоянной скоростью v относительно инерциальной К – системы отсчета. При каком значении скорости длина стрежня в этой системе отсчета будет на η = 0,5 % меньше его собственной длины?

153. Имеется прямоугольный треугольник с катетом a = 5,0 м и углом между этим катетом и гипотенузой . Найти в системе отсчета Кꞌ, движущейся относительно этого треугольника со скоростью = 0,866 с вдоль катета a (с – скорость света в вакууме): а) соответствующее значение угла ; б) длину гипотенузы и ее отношение к собственной длине .

154. Найти собственную длину стержня , если в К – системе отсчета (лабораторная система) его длина = 1,00 м, угол между стержнем и направлением движения α = 45^ои скорость = с /2, где с – скорость света в вакууме.

155. С какой скоростью двигались в К – системе отсчета часы, если за время t = 5,0 с (в К – системе) они отстали от неподвижных часов этой системы на = 0,10 с?

156. Собственное время жизни нестабильной частицы = 10 нс. Какой путь пролетит эта частица до распада в лабораторной системе отсчета, где ее время жизни = 20 нс?

157. В пунктах А и В на Земле, удаленных на расстояние = 10 км, произошли одновременно два события. Найти время, разделяющее эти события, с точки зрения наблюдателя на космическом корабле, удаляющегося от Земли вдоль прямой АВ со скоростью = 0,8 с (с – скорость света в вакууме).

158. Релятивистская частица с массой m и кинетической энергией Е _к налетает на покоящуюся частицу с такой же массой. Найти массу составной частицы, образовавшейся в результате соударения.

159. Релятивистская частица с массой m и кинетической энергией Е _к налетает на покоящуюся частицу с той же массой. Найти скорость составной частицы, образовавшейся в результате соударения.

160. Найти скорость частицы, кинетическая энергия которой Е _к = 500 МэВ и импульс Р = 865 МэВ/ с *, где с – скорость света.

161. При какой скорости кинетическая энергия частицы равна ее энергии покоя?

162. Найти скорость, при которой релятивисткий импульс частицы в n = 2 раза превышает ее ньютоновский импульс.

163. Сколько энергии (в расчете на единицу массы) надо затра- тить, чтобы сообщить первоначально покоившемуся космическому кораблю скорость = 0,980 с? (с – скорость света в вакууме).

164. Полная энергия мезона в n = 8 раз больше его энергии покоя. Найти скорость мезона.

165. Вычислить импульс протона с кинетической энергией Е _к = 500 МэВ.

166. На экваторе некоторой планеты тело весит в два раза меньше, чем на полюсе. Найти период обращения планеты около собственной оси. Плотность вещества планеты ρ = 3,0.10³кг/м³.

167. Телу сообщили на полюсе Земли скорость v ₀, направленную вертикально вверх. Зная радиус Земли и ускорение свободного падения на ее поверхности, найти высоту, на которую поднимется тело.

168. Найти радиус круговой орбиты стационарного спутника Земли, который остается неподвижным относительно ее поверхности. Какова скорость спутника?

169. Найти период обращения спутника, движущегося вокруг некоторой планеты вблизи ее поверхности, если средняя плотность планеты ρ = 3,3 г/см³.

КОНТРОЛЬНАЯ РАБОТА №2

⇐ Предыдущая12345Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: