 |
Единичный скачок. Единичный импульс.
|
|
|
|
Дискретное представление сигналов. Теорема отсчетов
Аналоговые сигналы в заданном диапазоне амплитуд принимают все значения и описываются непрерывными функциями времени. В соответствии с теоремой отсчетов аналоговый сигнал с ограниченным спектром полностью определяется своими дискретными значениями, взятыми через интервалы времени
, (1.13)
где 
– верхняя граничная частота в спектре сигнала.
Смысл теоремы в том, что для передачи по каналу связи непрерывного сигнала нет необходимости передавать все бесчисленное множество его значений, достаточно передать его отдельные мгновенные значения, отсчитанные через интервалы 
. По этим значениям функция может быть восстановлена на приёмном пункте единственным образом.
В соответствии с теоремой отсчетов функция s (t), описывающая аналоговый сигнал, может быть разложена в ряд вида:
, (1.14)
где:
– значения дискретных отсчётов функции в моменты времени 
;
- базисные ортогональные функции.
Представление непрерывного сигнала в соответствии с теоремой отсчетов показано на рис. 1.11.
| S (t) |
| Δ t |
| 2Δ t |
| 3Δ t |
| 4Δ t |
| 5Δ t |
| 6Δ t |
| t |
Рис. 1.11. Представление непрерывного сигнала по теореме отсчетов
В соответствии с рис. 1.11 непрерывную функцию можно представить в виде суммы дельта-импульсов, соответствующих моментам времени 
, умноженных на значения функции 
в эти моменты времени и пропущенных через идеальный фильтр нижних частот с граничной частотой 
. Напряжение на выходе такого фильтра при подаче на вход дельта-импульса в момент времени 
соответствует его импульсной характеристике
. (1.15)
Исходный непрерывный сигнал будет восстановлен после прохождения через фильтр всех дискретных отсчетов сигнала в результате суммирования функций 
.
|
|
|
На практике не существует сигналов с ограниченным спектром, так как все сигналы, ограниченные во времени, имеют бесконечную ширину спектра. Не существует также и идеальных фильтров. Поэтому исходный сигнал восстанавливается с некоторой погрешностью. При несоблюдении частоты дискретизации возможно наложение спектров дискретизированного сигнала.
В литературе эта теорема известна как теорема отсчетов Уиттакера-Найквиста -Шеннона-Котельникова.
Временной метод анализа сигналов
Суммируя по всем элементарным скачкам на интервале 
существования сигнала, и, переходя от суммы к интегралу, получим результирующее напряжение на выходе линейной цепи:
. (2.2)
Это соотношение известно как интеграл свертки или интеграл Дюамеля.
Сигналы на входе и выходе линейной цепи Таблица 2.1
| Воздействие на входе линейной цепи |
|
|
|
|
|
|
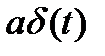
| Отклик на выходе линейной цепи |
|
|
|
|
|
|
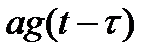
результирующее напряжение на выходе линейной цепи будет равно:
. (2.5)
Последнее выражение носит название интеграла Дюамеля в импульсной форме.
Этот интеграл является интегралом свертки двух функций 
и 
Импульсная характеристика линейной цепи связана преобразованиями Фурье с комплексным коэффициентом передачи линейной цепи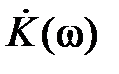 
следующим образом:
, (2.6)
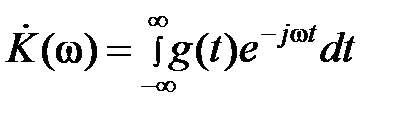. (2.7)
3
Единичный скачок. Единичный импульс.
Одной из задач радиоэлектроники является анализ прохождения электрических сигналов через линейные цепи. Зная форму входного и выходного сигналов, можно оценить свойства линейной цепи.
Линейной называется электрическая цепь, к которой применим принцип суперпозиции. В теоретическом курсе радиоэлектроники часто для упрощения анализа используют различного рода идеализации. В частности, для теоретического анализа воздействия детерминированных сигналов на линейные цепи используют математические модели идеальных электрических сигналов. Одним из таких сигналов является единичный скачок(рис.1.8).
|
|
|
Рис. 1.8. Единичный скачок
Единичный скачок, описывается функцией вида:
(1.7) Эту функцию называют функцией включения. Впервые эту функцию ввел английский физик Оливер Хевисайд (1850 - 1925). Реальный аналоговый сигнал можно приближенно представить некоторой суммой единичных скачков, возникающих в последовательные моменты времени. Устремив к нулю длительность интервала времени между единичными скачками, в пределе будет получена точная огибающая реального исходного сигнала. Такой способ представления сигналов называется динамическим (рис. 1.9).
Рис. 1.9. Динамическое представление сигнала с помощью единичных скачков
Если на вход линейной цепи подать напряжение в виде единичного скачка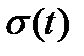 
, то изменение напряжения во времени на выходе цепи будет представлять ее переходную характеристику 
Единичный скачок является хорошим тестовым сигналом для исследования переходных характеристик линейных цепей. Поскольку единичный скачок является лишь математической моделью, которую экспериментально реализовать не представляется возможным, то при практическом исследовании линейных цепей используют периодические прямоугольные импульсы, анализируя реакцию линейной цепи на фронты и спады импульсов, которые условно можно считать единичными скачками противоположных знаков.
Другой способ представления реального сигнала использует математическую модель идеализированного сигнала в виде единичного импульса или дельта-импульса (d-импульса ) (рис. 1.10). В математической физике его еще называют функцией Дирака.
Рис. 1.10. Единичный импульс
Аналитически эта функция записывается следующим образом:
(1.8)
Кроме того:
. (1.9)
Отсюда следует связь между единичным скачком и единичным импульсом:
. (1.10)
Если на вход линейной цепи подать напряжение в виде единичного импульса, то изменение напряжения во времени на выходе цепи будет представлять собой импульсную характеристику 
Понятие 
импульса используется в радиоэлектронике при исследовании воздействия очень коротких импульсов напряжения на линейные цепи. При этом не обязательно, чтобы длительность реального сигнала была бесконечно мала, а амплитуда бесконечно велика. Достаточным является условие, чтобы длительность импульса была много меньше постоянной времени цепи.
|
|
|
Реальный сигнал можно представить некоторой суммой единичных импульсов, возникающих в последовательные моменты времени. Эти импульсы примыкают непосредственно друг к другу и вписываются в огибающую исходного сигнала.
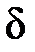-импульс обладает стробирующим свойством. Стробирование – получение значения сигнала в заданный момент времени.
Рассмотрим 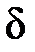- импульс, сдвинутый по оси времени на 
:
(1.11)
Для некоторой непрерывной функции можно записать:
. (1.12)
Последнее выражение получено, исходя из того, что функция 
равна нулю везде, кроме точки 
. Стробирующее свойство 
функции используется в аналого-цифровых преобразователях при дискретизации сигналов.
4
|
|
|
