 |
Использование t-статистики для проверки статистических гипотез о параметрах регрессии.
|
|
|
|
Вопрос 1
Множественная линейная регрессия является обобщением парной линейной регрессии на несколько объясняющих переменных. При выполнении предпосылок Гаусса-Маркова оценки параметров уравнения множественной линейной регрессии, полученные методом наименьших квадратов, обладают свойствами несмещенности, эффективности и состоятельности. Статистическая значимость коэффициентов и качество подбора уравнения проверяются с помощью распределений Стьюдента и Фишера. Коэффициент при объясняющей переменной показывает, на сколько единиц изменится зависимая переменная, если объясняющая вырастет на одну единицу при фиксированном значении остальных объясняющих переменных. В случае множественной регрессии дополнительно предполагается отсутствие мультиколлинеарности объясняющих переменных.
Вопрос 2
В основе метода наименьших квадратов (МНК) лежит поиск таких значений коэффициентов регрессии, при которых сумма квадратов отклонений теоретического распределения от эмпирического была бы наименьшей.
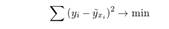
Оценки коэффициентов моделей, полученные на основе МНК, не зависят от фактического закона распределения.
В отношении свойств ошибки модели выдвигаются следующие предположения:
– ошибка имеет нулевое математическое ожидание;
– ее дисперсия конечна и постоянна;
– автокорреляционные связи в ряду ошибки отсутствуют
– ряд значений ошибки статистически не связан с рядами значений независимых переменных модели.
Геометрическая интерпретация МНК
Геометрически задача МНК состоит в том, чтобы найти такой вектор у^ из £(Х), чтобы евклидово расстояние между у и у^ было минимальным. Иными словами, мы ищем среди всех линейных комбинаций регрессоров наиболее близкую к y. 
|
|
|
Теорема Гаусса-Маркова
Если предпосылки метода наименьших квадратов, то оценки, полученные по МНК, обладают следующими свойствами:
1. Оценки параметров являются несмещенными, т. е. M(b1) = β1, M(b0) = β0 (математические ожидания оценок параметров равны их теоретическим значениям). Это вытекает из того, что M(εi) = 0, и говорит об отсутствии систематической ошибки в определении положения линии регрессии.
2. Оценки параметров состоятельны, так как дисперсия оценок параметров при возрастании числа n наблюдений стремится к нулю D(b0) → 0, D(b1) → 0 при n → ∞. По другому говоря, при увеличении объема выборки надежность оценок увеличивается (b1 наверняка близко к β1, b0 — близко к β0).
3. Оценки параметров эффективны, т. е. они имеют наименьшую дисперсию по сравнению с другими оценками данных параметров, линейными относительно величин yi.
Предпосылки МНК (Условия Гаусса-Маркова):
1. Математическое ожидание случайного отклонения еi равно нулю: M(еi) = 0 для всех наблюдений.
2. Дисперсия случайных отклонений epsiloni постоянна: D(εi) = D (εj) = σ2 = const для любых наблюдений i и j.
3. Случайные отклонения εi и εj являются независимыми друг от друга для i ≠ j.
4. Случайное отклонение должно быть независимо от объясняющих переменных.
5. Модель является линейной относительно параметров.
6. Отсутствие мультиколлинеарности.
7. Случайные отклонения εi, i = 1, 2,..., n, имеют нормальное распределение.
Использование t-статистики для проверки статистических гипотез о параметрах регрессии.
Для проверки нулевой гипотезы Н0 о равенстве нулю некоторого коэффициента регрессионного уравнения (Н0: β=0) необходимо сравнить фактическое значение статистики, которое указывается в колонке t-Statistic, с критическим значением t-статистики Стьюдента для выбранного уровня значимости ε, то есть со значением двусторонней (1-ε) квантили t-статистики Стьюдента с n-k степенями свободы. Двусторонняя квантиль может быть найдена с использованием команды show@qtdist(v,p).
|
|
|
Если фактическое значение t -статистики Стьюдента больше критического значения статистики, то нулевая гипотеза отвергается для данного уровня значимости ε, иначе нулевая гипотеза не может быть отвергнута для данного уровня значимости ε.
В случае отклонения нулевой гипотезы для уровня значимости ε говорят, что коэффициент β i регрессионного уравнения значим на уровне значимости ε (или, говорят, что оценка коэффициента β i значимо отличается от нуля), и соответствующий ему регрессор объясняет вариацию зависимой переменной. В противном случае говорят, что коэффициент незначим на уровне значимости ε.
6. Использование коэффициента детерминации R2 и F–критерия для проверки статистических гипотез о параметрах регрессии.
Коэффициент детерминации даёт количественную оценку меры анализируемой связи. Он показывает часть вариации результативного признака, который находится под влиянием факторов, которые изучаются, то есть определяет, какая частица вариации признака Y учитывается в модели и обусловлена влиянием на неё независимых факторов.
Величина 0<R2<2. Чем ближе R2 к 1, тем точнее модель. Если R2>0,8, то модель считается точной, если R2<0,5, то модель надо улучшить, либо выбрав другие факторы, либо увеличив количество наблюдений.
Чаще всего, давая интерпретацию коэффициента детерминации, его выражают в процентах. R2=0.982=0.9596, т.е. в 95,96% случаев изменения х приводят к изменению у. Другими словами – точность подбора уравнения регрессии – высокая. Остальные 4.04% изменения Y объясняются факторами, не уточнёнными в модели.
Скорректированный коэффициент детерминации применяется для решения двух задач: оценки реальной тесноты связи между результатом и факторами и сравнения моделей с разным числом параметров. В первом случае обращают внимание на близость скорректированного и нескорректированного коэффициентов детерминации. Если эти показатели велики и различаются незначительно, модель считается хорошей. При сравнении разных моделей предпочтение при прочих равных условиях отдаётся той, у которой больше скорректированный коэффициент детерминации.
|
|
|
Для проверки нулевой гипотезы о значимости уравнения в целом используют статистику Фишера F. В этом случае нулевая гипотеза имеет вид Н0: (β1=β2=…=0). Необходимо сравнить фактическое значение статистики Фишера F и сравнить его с критическим значением статистики Фишера F для выбранного уровня значимости ε, то есть со значением (1-ε) квантили статистики Фишера с (n-k, k-1) степенями свободы, которую можно найти с помощью команды show @qfdist(v,p1,p2), где v =1-ε, p1 = n*k, p2 = k -1.
Если фактическое значение статистики Фишера F больше критического значения, то нулевая гипотеза отвергается для данного уровня значимости ε, иначе нулевая гипотеза не может быть отвергнута для данного уровня значимости ε.
В случае отклонения нулевой гипотезы для уровня значимости ε говорят, что регрессионное уравнение значимо в целом на уровне значимости ε и вариация независимых переменных объясняет вариацию зависимой переменной в регрессионном уравнении. В противном случае говорят, что уравнение в целом незначимо на уровне значимости ε и включенные в регрессию факторы не улучшают прогноз для зависимой переменной по сравнению с ее средним значением.
|
|
|


