 |
Режимы работы линейной электрической цепи: короткого замыкания (КЗ) и холостого хода (ХХ)
|
|
|
|
Введение
Материал, изложенный в рассматриваемом методическом пособии, посвящен аналитическому анализу линейной электрической цепи, работающей на непрерывно изменяющуюся линейную нагрузку.
В данном пособии рассматриваются: граничные режимы данной цепи, а так же режим согласования, и их энергетические параметры. Особое место в данном пособии уделено рассмотрению пожароопасного режима – режиму короткого замыкания.
Анализ граничных режимов исходной линейной электрической цепи, выполненный с применением соответствующего математического аппарата, позволяет обосновать «существование» идеализированных источников: источника ЭДС, источника тока.
Идеализированные источники нашли широкое применение в курсе дисциплины «Электроника» и служат базисом при проведении расчетов электронных схем с использованием пакетов прикладных программ для персональных вычислительных машин – персональных компьютеров (ПК).
В данном пособии показана взаимосвязь методов высшей математики и физики, применяющихся при аналитическом анализе линейной электрической цепи, и на этой основе получены обоснованные закономерности: энергетических режимов функционирования линейной электрической цепи.
Коллектив авторов, излагая материал, представленный в данном пособии, исходил из того, что читатель в полной мере владеет математическим аппаратом в объеме первого курса «Высшей математики» и творчески освоил следующие разделы курса общей физики: “Механика. Электричество и магнетизм“.
В данном пособии методами математического анализа исследуется функция 
, которая возникает в процессе изучения линейной электрической цепи. Подробное исследование указанной функции выполнено впервые. Это исследование, выполненное А. Г. Степановым, позволяет обосновать инженерно – физический подход, направленный на достижение максимального значения коэффициента полезного действия цепи: в практическом плане достаточно близкого к его максимальному значению. Это же исследование позволяет наметить дальнейший путь теоретических исследований с целью обоснования существования критерия, необходимого для инженерного моделирования режима холостого хода, без использования режима “обрыва“ ветви, содержащей пассивный приемник электрической энергии.
|
|
|
Творческое освоение слушателями, магистрами, курсантами, студентами дисциплины «Электротехника и электроника», позволит им в дальнейшем учебном процессе успешно изучить целый ряд дисциплин специального профиля.
Особую благодарность А. Г. Степанов выражает д.т.н., профессору
С.В.Пузач - начальнику кафедры инженерной теплофизики и гидравлики, полковнику внутренней службы А Г ПС МЧС России, за конструктивные научные рекомендации и творческое сотрудничество.
Режимы работы линейной электрической цепи, состоящей из реального источника электродвижущей силы ЭДС и
Изменяющейся во времени линейной нагрузки.
Энергетические характеристики режимов цепи
Режимы работы линейной электрической цепи: короткого замыкания (КЗ) и холостого хода (ХХ)
Рассмотрим следующую линейную цепь, схема которой приведена на рис. 1.
Рис. 1. Схема линейной электрической цепи:
Е - электродвижущая сила (ЭДС), [В]; r 0 – внутреннее сопротивление источника ЭДС, [Ом];
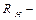- сопротивление нагрузки, [Ом]; (1), (2), (3) – положения движка переменного резистора.
Запишем исходные данные для данной линейной электрической цепи:
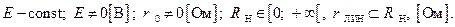
Предположим, что в начальный момент времени движок (3) переменного нагрузочного резистора находится в среднем состоянии между двумя предельными состояниями (1) и (2).
|
|
|
Каждое из возможных состояний характеризует собой определенный режим функционирования всей цепи, обусловленный величиной нагрузочного резистора с сопротивлением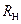 
.
Необходимо определить каждый из возможных режимов цепи и соответствующие им энергетические характеристики (параметры).
Следует внести несколько дополнительных пояснений, касающихся граничных режимов функционирования анализируемой цепи.
Если движок находится в состоянии (1), то это фактически соответствует исключению нагрузки, т.е. ее закорачиванию. Отсюда, название режима – «короткое замыкание» (КЗ).
Если движок находится в состоянии (2), то при большой величине сопротивления нагрузки это эмиттирует другой возможный граничный режим – “ холостого хода” (ХХ).
Если переменный резистор, как элемент электрической цепи, используется с целью изменения величины тока, протекающего в данной ветви, то говорят, что переменный резистор включен, как реостат.
Если переменный резистор, предназначен для изменения величины разности потенциалов между данной точкой электрической цепи и точкой, потенциал которой равен нулю, то считается, что переменный резистор включен как потенциометр.
Необходимо сделать дополнение: в некоторой точке электрической цепи ее потенциал либо фактически равен нулю, т.е., эта точка “заземлена“, либо ее потенциал условно принимается равным нулю.
Если движок переменного резистора находится в состоянии (3) - среднее значение величины переменного резистора, то по закону Ома, можно записать следующее выражение для тока, протекающего в рассматриваемой цепи:
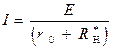
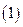
Выбор структуры анализируемой цепи, представленной на рисунке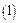 
, можно объяснить следующим образом.
В состав современных технических систем, входят, как правило, в виде элементов этих систем, например, линии проводной связи, компьютерные сети, которые построены без использования волоконно-оптических линий связи (ВОЛС). В силу воздействия на эти элементы систем, ряда специальных факторов: таких, например, как электромагнитное, создаваемое грозовой активностью, температурным фронтом, возникающим при пожаре и целым рядом других факторов, отмечается изменение величин сопротивлений изоляции у данных элементов.
|
|
|
Поэтому величина тока, протекающего через эти элементы, в ряде случаев, зависит не только от величины приемника электрической энергии, но и величины сопротивления их изоляции. При этом величина сопротивления изоляции в каждом конкретном случае, способна уклоняться от своего номинального значения, в силу специальных факторов, в общем, по нелинейному закону. Линейный закон изменения величины сопротивления изоляции наблюдается лишь, как частный случай, при достаточном числе ограничений, дополнительно вводимых, а поэтому его следует рассматривать лишь как самое первое приближение при изучении этого явления.
В проводимом ниже аналитическом исследовании линейной электрической цепи, предполагается, что величина сопротивления изоляции линии передачи учитывается в величине потребителя (приемника) электрической энергии.
В действительности, изменение величины сопротивления изоляции у потребителя (приемника) вероятно должно происходить по линейному закону, если в качестве ограничений, изначально вводимых, принять: постоянство температуры окружающей среды, постоянство величины ее давления, постоянство ее влажности, отсутствие механической деформации изоляции и кроме того отсутствие воздействия специальных факторов.
Определим для каждого из указанных выше режимов линейной электрической цепи энергетические параметры (характеристики) цепи и построим графики, соответствующие этим параметрам.
Режим короткого замыкания
Режимом короткого замыкания (КЗ) электрической цепи, называется такой режим, при котором величина сопротивления нагрузки стремиться к нулю, а величина тока, протекающего через нагрузку, стремиться к максимально возможному значению.
В приведенном определении по существу содержатся необходимое и достаточное условие, характеризующее собой режим короткого замыкания. При нашем дальнейшем изложении материала, в некоторых математических соотношениях, над знаком равенства будет записано сокращение 
, - указывающее на то, что данное соотношение записано в силу определения.
|
|
|
Опираясь на определение режима КЗ, и используя соотношение (1), получим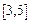 
аналитическое выражение для тока в цепи для рассматриваемого режима:
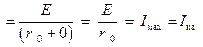
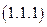
Прежде чем получать аналитические выражения для различных мощностей в рассматриваемой цепи, с учетом режима КЗ, укажем, как определяется мощность источника электрической энергии – источника ЭДС в линейной электрической цепи.
Мощность источника электродвижущей силы определяется как произведение величины источника ЭДС на величину тока, протекающего через этот источник.
Запишем выражение для мощности PE источника ЭДС, с учетом данного выше определения, применительно к режиму короткого замыкания (КЗ):
, 
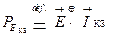где графический символ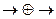 
означает, что условно выбранное положительное направление тока в рассматриваемой цепи, совпадающее с направлением тока КЗ, сонаправлено ЭДС источника.
Осуществив подстановку выражения (1.1.1) в выражение (1.1.2), мы получим соотношение для мощности источника в режиме КЗ и учитывающее параметры исследуемой (анализируемой) цепи:
Из полученного соотношения (1.1.3) следует, что в режиме КЗ значение мощности источника ЭДС определяется по квадратичному закону.
В дальнейшем изложении будет использоваться выражение (1.1.3) для построения графика зависимости мощность источника ЭДС от изменяющей величины резистора нагрузки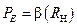 
(рис. 3).
Найдем аналитическое выражение для P 0 КЗ - мощности потерь на внутреннем (r 0) сопротивлении источника ЭДС в режиме короткого замыкания.
С этой целью, целесообразно воспользоваться законом Джоуля – Ленца, для рассматриваемого режима. Выражение закона Джоуля – Ленца для данного случая принимает следующий вид:
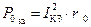
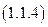
Подставив, в соотношение (1.1.4) выражение для тока короткого замыкания, взятое из соотношения (1.1.1), находим:
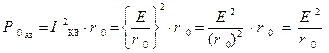
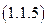
Полученное выражение (1.1.5) указывает, что значение мощности потерь, представляющей скорость преобразования электрической энергии в тепловую энергию, и выделяющуюся на внутреннем сопротивлении источника ЭДС в режиме КЗ, также подчиняется квадратичному закону 
.
Следующий пункт нашего исследования состоит в определении аналитического выражения для мощности, выделяющейся на сопротивлении нагрузки (Р нКЗ) в рассматриваемом режиме, и нахождении ее значения.
Аналитическое выражение закона Джоуля – Ленца для данного режима имеет следующий вид:
.
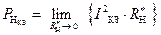
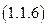Учитывая, определение режима КЗ, и принимая во внимание соотношение (1.1.1), из соотношения (1.1.6) находим :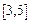
.
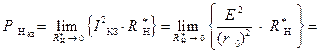
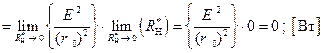
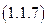Из выражения (1.1.7) следует, что значение мощности потерь на резистивном элементе, обладающего сопротивлением, в режиме КЗ равно нулю. Отметим, что этот результат, можно так же получить и чисто качественно, используя для этой цели, лишь определение режима КЗ.
|
|
|
Определим наиважнейший из энергетических параметров цепи в режиме КЗ - коэффициент полезного действия (КПД) 
.
Напомним соотношение, определяющее коэффициент полезного действия, взятое нами из курса “Механика“:
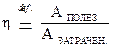
В одном основополагающем разделе линейных электрических цепей, а именно – разделе, посвященном “Электростатике”, важнейшее физическое понятие - понятие работы, связано с энергетической характеристикой электростатического поля – потенциалом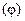 
, следующим соотношением 
:
. 
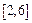Из соотношения (1.1.9), находим
.
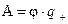
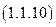Выполнив, почленное деление левой и правой частей соотношения (1.1.10) на время (t), отличное от нуля, находим самое общее выражение для мощности:
.
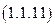В классической механике для понятия мощности существуют два аналитических выражения:
а) в одном из этих выражений, мощность трактуется как физическая величина, которая определяется значением постоянства работы, совершенной в единицу времени:
; 
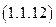
б) в другом из этих выражений, мощность трактуется как физическая величина, характеризующая собой скорость совершаемой работы во времени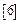 
:
. 
Следует отметить, что в электрических цепях постоянного тока используется лишь соотношение (1.1.12), в то время, как в цепях переменного тока, в общем случае, применяются оба этих соотношения, а соотношение (1.1.3) используется лишь в цепях переменного синусоидального тока, представляющих собой частный случай.
Если к цепи постоянного тока применить соотношения (1.1.11, 1.1.12), то можно аналитически выразить мощность через работу:
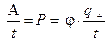
Используя базисную форму записи для постоянного тока:
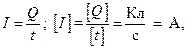
и выражение 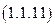, найдем аналитическое выражение мощности, содержащее наиглавнейшие параметры цепи постоянного тока:
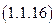
Используя выражение закона Ома, записанного для пассивного участка цепи, найдем :
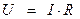
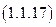
Подставив соотношение (1.1.17) в соотношение (1.1.16), получим аналитическое выражение для закона Джоуля - Ленца:
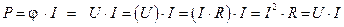
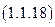
Соотношения 
, приведенные выше, позволили осуществить вывод закона Джоуля – Ленца, основываясь при этом на интегральную форму записи следующих физических понятий: мощности, тока и на применение закона Ома для участка цепи.
Применение выражения (1.1.18), позволяет записать в общем виде математическое соотношение для коэффициента полезного действия (КПД) в режиме короткого замыкания:
.
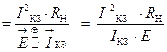
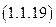Опираясь на соотношение 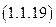, можно провести физическое истолкование понятия коэффициента полезного действия для рассматриваемой линейной электрической цепи, вне зависимости от режима ее функционирования.
Под коэффициентом полезного действия в рассматриваемой линейной электрической цепи следует понимать отношение величины мощности, выделяющейся на нагрузке, к мощности, развиваемой источником энергии.
Учитывая, что величина тока короткого замыкания, и величина источника ЭДС отличны от нуля, и выполняя последовательно процедуру деления числителя и знаменателя выражения (1.1.19), на эти величины, найдем другое соотношение для 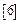коэффициента полезного действия данного режима, выражающее его через исходные параметры самой цепи:
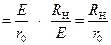
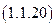
Осуществив процедуру предельного перехода в соотношении (1.1.20), найдем значение КПД для режима КЗ:
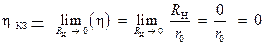
Вывод:
Режим короткого замыкания является критически опасным: при этом режиме вся мощность, поставляемая источником в цепь, выделяется на внутреннем омическом сопротивлении самого источника.
При такой внештатной ситуации происходит преобразование электрической энергии в тепловую энергию исключительно на внутреннем сопротивлении источника энергии. Физически такое явление характеризует разрушение источника энергии и является основной причиной возникновения пожароопасной обстановки.
Необходимо, отметить, что уже существуют разработанные и внедренные в инженерную практику устройства, которые в значительной мере успевают отреагировать на тепловое воздействие, возрастающего в цепи тока.
Эти устройства и их конструктивные особенности, и важнейшие параметры будут подробно рассмотрены в курсе “Пожарная безопасность электроустановок “.
Режим холостого хода
Режимом холостого хода (ХХ) электрической цепи, называется такой ее режим функционирования, при котором величина сопротивления нагрузки стремиться к бесконечности, а величина тока, протекающего через нагрузку, стремиться к нулю.
В приведенном определении по существу содержатся необходимое и достаточное условия, характеризующие собой режим холостого хода.
Используя определение режима холостого хода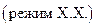 
, и применяя закон Ома для полной цепи (1), напишем аналитическое выражение 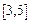для тока в анализируемом режиме 
:
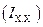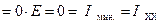
Проводя аналогию с раннее рассмотренным режимом короткого замыкания, можем записать аналитическое выражение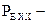 
для мощности источника ЭДС в режиме холостого хода:
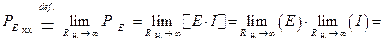
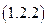
Применение такой методики позволяет составить аналитическое выражение для мощности, выделяющейся на нагрузке в рассматриваемом режиме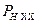 
:
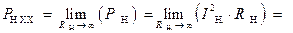
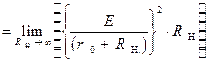
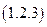
Аналитическое выражение для мощности потерь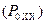 
- мощности, выделяющейся на внутреннем сопротивлении 
источника ЭДС, имеет вид:
.
Применяя соотношения (1.2.2) и (1.2.3), находим значение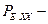 
мощности источника ЭДС в режиме холостого хода:
.
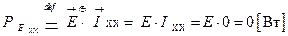
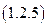Физическое содержание полученного значения соотношения (1.2.5) состоит в следующем: если в режиме ХХ величина сопротивления нагрузки бесконечно большая, что соответствует разомкнутой (обрыву) ветви, содержащей нагрузку, то ток в рассматриваемой цепи, равен нулю, а поэтому равна нулю и мощность, вырабатываемая источником электродвижущей силы.
Определим значение 
мощности потерь на внутреннем сопротивлении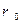 
самого источника ЭДС:
.
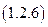Применение закона Джоуля – Ленца, позволяет записать аналитическое выражение для мощности, выделяющейся на нагрузке в режиме холостого хода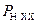 
:
.
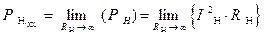
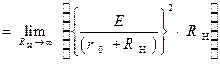
Для анализа соотношения (1.2.7) целесообразно воспользовавшись следующими теоремами, известными читателю из курса дифференциального исчисления, вот эти теоремы: о нахождении предела произведения, вычислении предела дроби, онахождении предела степени:
.
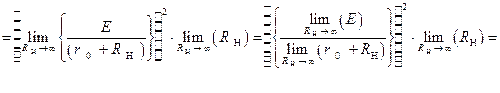
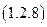Итак, в соотношении (1.2.8) получается неопределенность следующего вида: 0·∞.
Раскроем эту неопределенность двумя способами. Первый способ раскрытия неопределенности вида 0·∞ математический. Из курса математического анализа известно, что неопределенность указанного вида, раскрывается с помощью метода сведения этой неопределенности к неопределенностям 
следующих видов: 
.
Другими словами, необходимо, свести к одному из указанных видов неопределенностей, неопределенность, полученную нами в соотношении (1.2.8):
.
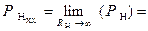
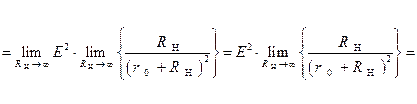
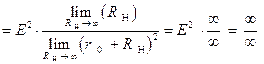
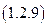Полученное соотношение (1.2.9) представляет собой неопределенность требуемого нам вида, а именно вида: 
.
Полученную неопределенность можно так же раскрыть следующими двумя методами.
Оба этих метода относятся к математическим методам. Первый метод 
это метод раскрытия неопределенности видов: с использованием правила Иоганна Бернулли – Лопиталя .
Напомним кратко математическую сущность правила Иоганна Бернулли - Лопиталя. При определении предела непрерывной функции часто, в результате подстановки предельного значения аргумента этой функции, приходят к неопределенностям следующих видов:
.
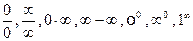Нахождение предела функции в таких случаях называют раскрытием неопределенности. Теорема, которая приводится ниже, исторически известная под правилом Лопиталя, представляет собой математический базис, позволяющий раскрывать указанные выше две первые неопределенности, т. е, неопределенности вида: 
. Справедливости ради, необходимо отметить, что маркиз де Лопиталь был единственным учеником у выдающегося швейцарского математика Иоганна Бернулли. Именно благодаря Иоганну Бернулли, маркиз де Лопиталь получил систематические сведения о тогда еще новом направлении в математике – анализе бесконечно малых.
В последствие, из этого ученья возникло стройное, логичное, гармоничное направление математики, получившие название – математический анализ. Математический анализ объединяет в себе два направления: дифференциальное и интегральное исчисление.
Следует отметить, что маркиз де Лопиталь тщательно законспектировал лекции и в последствие издал их отдельной книгой, в виде первого учебника по дифференциальному исчислению в Европе: это историческое событие произошло в 1696 году, когда маркиз Лопиталь выпускает в Париже под своим именем первый в истории учебник под названием: «Анализ бесконечно малых для исследования кривых линий» (на французском языке), в основу этой книги была положена первая часть конспекта Иоганна Бернулли.
Именно в силу того обстоятельства, что Лопиталь был учеником Иоганна Бернулли, историки математики, стали правило Лопиталя называть правилом И. Бернулли – Лопиталя. Ниже 
приводится формулировка теоремы, которая иллюстрирует собой правило И. Бернулли – Лопиталя.
Теорема.
Если существуют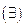 
две функции 
, такие, что для них выполняются следующие условия:
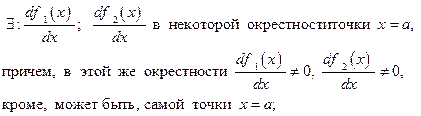
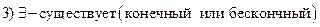
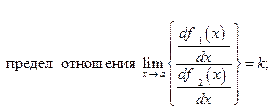
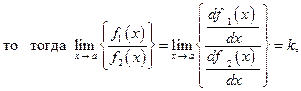
т.е., когда обе рассматриваемые функции непрерывны и дифференцируемые,
то предельные значения этих функции соответственно равны:
,
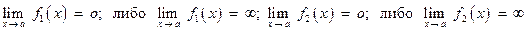а отношения этих функций имеют следующий вид:
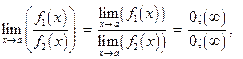
то тогда указанные неопределенности можно раскрывать по правилу И.Бернулли - Лопиталя:
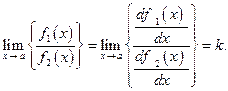
Приведенная нами выше теорема остается в силе и в том случае, если ее условие 
, будет заменено на условие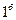 
:
т.е., теорему можно применять к раскрытию неопределенностей вида .
Во всех условиях этой теоремы предел можно понимать как односторонний. Эта теорема справедлива так - же для односторонних пределов и в случае, когда предельное значение варианты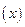 
, т.е.,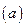 
обозначает собой также и бесконечность.
Применим к выражению 
, взятому из ранее полученного соотношения (1.2.7), правило И.Бернулли - Лопиталя, в результате этого, найдем:
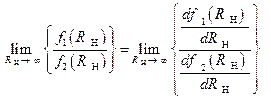
В записанном соотношении , соответствующие функции 
,
равны:
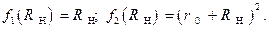
Выполнив процедуру дифференцирования каждой из указанных функций,
получим:
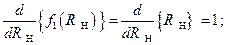
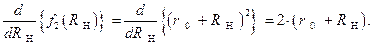
Тогда, применение правила И.Бернулли - Лопиталя к соотношению , позволит раскрыть указанную выше неопределенность :
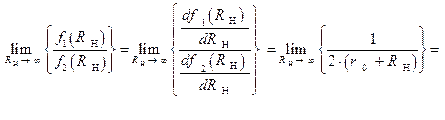
Приведем еще один математический метод , позволяющий раскрывать неопределенности вида .
В соотношении до выполнения предельного перехода осуществим тождественные преобразования над выражением, находящимся под знаком предела. Используя формулу сокращенного умножения для квадрата суммы
двух чисел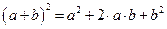 
, мы получим:
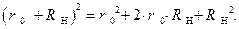
Тогда, выражение, стоящее под знаком предела, будет иметь следующий
вид:
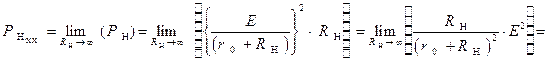
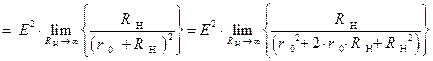
До осуществления предельного перехода, выполним процедуру деления выражения, стоящего под символом предела в соотношение , на наивысшую степень варианты R2н, после этого получим:
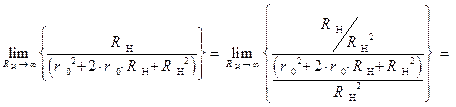
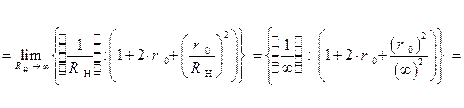
Сопоставляя результат выражения 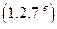с результатом выражения, приходим к выводу, что они равны между собой.
Укажем, кроме того, еще один метод раскрытия полученной неопределенности.
Этот физический метод основан на применение второго закона Кирхгофа, который непосредственно вытекает из закона сохранения энергии.
В силу применения второго закона Кирхгофа имеем:
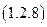
Умножая левую и правую часть соотношения (1.28) на значение тока холостого хода, получим:
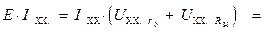
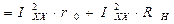
Принимая во внимание полученные нами ранее соотношения (1.2.3) и (1.2.4), в силу которых:
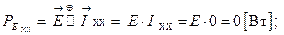
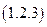
можем переписать соотношение (1.29) в равносильном виде:
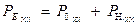
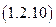
Используя записанное 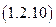соотношение, найдем, следуя физическому подходу, величину мощности нагрузки в режиме ХХ.
Из соотношения (1.2.10), находим мощность в нагрузке для режима ХХ:
.
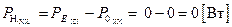
Все три метода, примененные к раскрытию неопределенности вида , дали один и тот же результат.
Определим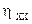 
КПД для режима холостого хода (ХХ).
По аналогии с соотношением (1.1.20) запишем выражение, определяющее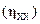 
:
.
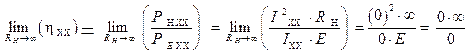
Полученное соотношение 
, с математической точки зрения, представляет собой удвоенную неопределенность, возникшую в результате осуществления предельного перехода, т.е., при нахождении предела от аналитического выражения, которое определяет собой КПД для режима холостого хода, который математически компактно можно записать следующим образом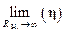 
.
В числителе последнего соотношения удвоенная неопределенность возникла вследствие того, что, когда величина резистивного элемента, представляющего собой линейную нагрузку, безгранично возрастает, т.е., когда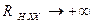 
, то тогда вместе с этим безгранично уменьшается величина тока в цепи, т. е, имеет место выражение 
.
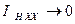Раскрывать удвоенную неопределенность, можно с помощью тождественных преобразований, выполняющимися над выражением, стоящим под символом предела .
.
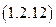Осуществив предельный переход в полученном 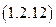выражении, найдем значение КПД для рассматриваемого режима:
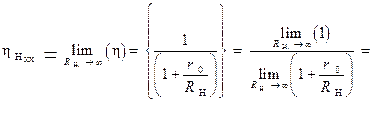
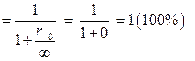
Определим, геометрический характер зависимости 
с целью дальнейшего построения соответствующего графика. Для этого выполним процедуру деления “уголком“ следующего выражения:
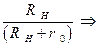
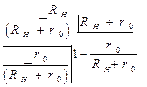
Выполнив процедуру предельного перехода в последнем соотношении (1.2.14), найдем числовое значение КПД цепи, функционирующей в режиме ХХ:
Выводы по режиму холостого хода (ХХ):
1) в режиме ХХ рассматриваемая нами линейная электрическая цепь
имеет максимальное значение КПД, численно равное единице;
2) аналитически геометрический характер зависимости подчиняется гиперболическому закону ( рис. 3);
Общий вывод для двух ранее рассмотренных режимов КЗ и ХХ.
Рассматриваемая линейная электрическая цепь, как в режиме КЗ, так и в режиме ХХ, имеет одинаковые значения для мощности в нагрузке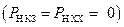 
.
Режим холостого хода рассмотрен в данной лекции с учетом того, что этот режим широко использовался в курсе «Электротехника и электроника».
Данный режим использовался, как при рассмотрении опыта по испытанию трансформатора, так и при исследовании частотных характеристик реактивных элементов, входящих в состав последовательного колебательного контура, с одной стороны, так и при исследовании амплитудно – частотной и фазо – частотной характеристик контура, с другой стороны.
В лекциях по дисциплине “Электроника“ режим ХХ так же получил свое применение, там в частности, он используется в методе эквивалентного генератора, служащего для расчета электронных схем, функционирующих в линейном ре
|
|
|
