 |
Режим согласованной нагрузки
|
|
|
|
В результате проведенного выше анализа, нами было установлено, что в рассматриваемой цепи, существуют два граничных режима ее функционирования: режим – КЗ и режим ХХ. Переход от одного граничного режима цепи к другому граничному режиму, осуществляется за счет непрерывного изменения положения движка реостата; но в тоже время, величины мощностей в нагрузке для этих режимов совпадают.
Тогда, в соответствии с теоремой Мишеля Ролля  , известной из курса дифференциального и интегрального исчисления, следует; что существует такое состояние движка реостата, при котором скорость изменения величины мощности в нагрузке будет равна нулю.
, известной из курса дифференциального и интегрального исчисления, следует; что существует такое состояние движка реостата, при котором скорость изменения величины мощности в нагрузке будет равна нулю.
Нам, для рассматриваемого режима, необходимо, определить следующие энергетических параметры: мощность в нагрузке, мощность потерь на внутреннем сопротивлении источника Э.Д.С., К.П.Д. цепи.
Напомним содержание теоремы Мишеля Ролля, известное читателю из курса дифференциального исчисления.
Если существует функция  , обладающая следующими свойствами
, обладающая следующими свойствами  :
:
 то существует точка
то существует точка  , принадлежащая указанному отрезку [a,b], такая, что имеет место следующее соотношение:
, принадлежащая указанному отрезку [a,b], такая, что имеет место следующее соотношение:  .
.
Для лучшего восприятия (напоминания) теоремы Мишеля Ролля ниже приведен рисунок, иллюстрирующий эту теорему.

В нашем случае:  .
.
В ходе дальнейшего рассуждения будем считать, что 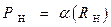 функция, подлежащая дифференцированию при условии выполнении следующих условий: величина резистора нагрузки, принадлежит полуоткрытому интервалу
функция, подлежащая дифференцированию при условии выполнении следующих условий: величина резистора нагрузки, принадлежит полуоткрытому интервалу  ; а значение производной определяется с учетом равенства
; а значение производной определяется с учетом равенства  . В самом общем случае, это можно записать в следующем вид:
. В самом общем случае, это можно записать в следующем вид: 
Перепишем левую часть последнего выражения в развернутом виде, а затем выполним процедуру дифференцирования  :
:
|
|
|





 .
.
Полученное нами выше соотношение (1.3.1) для выражения производной первого порядка приравнивается к нулю, с целью определения критической точки первого рода  :
:


 .
.
Необходимо обратить внимание, на то, что в выражении  , не проводилась процедура сокращения числителя и знаменателя на их общий сомножитель
, не проводилась процедура сокращения числителя и знаменателя на их общий сомножитель  .
.
Это было сделано специально, для того, чтобы в дальнейшем не потерять частное решение системы (1.3.2), имеющее важное физическое содержание. Из последней системы непосредственно следует:



 .
.
Соотношение  можно переписать в следующем равносильном виде:
можно переписать в следующем равносильном виде:
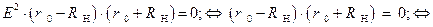

 .
.
Последнее соотношение  , записанное в виде дизъюнкции, обозначает, что в анализируемой линейной электрической цепи, имеют место лишь следующие вариации: либо
, записанное в виде дизъюнкции, обозначает, что в анализируемой линейной электрической цепи, имеют место лишь следующие вариации: либо

 ,
,
либо


Из соотношений  ,
,  полученных нами выше, находим:
полученных нами выше, находим:

 ,
,
либо


Каждому из полученных выше соотношений(1.3.4), (1.3.5), дадим физическое истолкование.
Физическое истолкование начнем, однако, не с соотношения  , а с соотношения
, а с соотношения  , как более необычного и требующего к себе более пристального внимания.
, как более необычного и требующего к себе более пристального внимания.
Соотношение  указывает на два возможных события:
указывает на два возможных события:
1) либо нагрузка имеет отрицательное сопротивление;
2) либо внутреннее сопротивление самого источника отрицательно.
Выясним: возможны ли эти события в линейной электрической цепи, анализируемой нами  . Здесь, следует отметить, лишь то, что оба эти события по своей математической сущности – взаимозависимые, поэтому, достаточно, установить либо возможность существования одного из них, либо опровергнуть такую возможность.
. Здесь, следует отметить, лишь то, что оба эти события по своей математической сущности – взаимозависимые, поэтому, достаточно, установить либо возможность существования одного из них, либо опровергнуть такую возможность.
Из курса “ Электротехника и электроника “, который был прочитан и поэтому курсу был сдан экзамен (дифференцированный зачет), читатель (слушатель), вероятно, помнит, что в любой линейной электрической цепи постоянного тока, источник э.д.с., может теоретически функционировать сколь угодно долго, в одном из двух режимов: либо в режиме генератора, либо – в режиме потребителя.
|
|
|
Поэтому, для последующего вывода, нам потребуются лишь напомнить два определения, характеризующие собой, эти режимы функционирования источника э.д.с. в линейной электрической цепи.
Приведем (напомним) определение “генераторного“ режима для источника э.д.с. 
Источник э.д.с. функционирует в режиме “генератора”, тогда и только тогда, когда величина мощности, поставляемая им в нагрузку и определяемая по соотношению  больше нуля.
больше нуля.
В приведенной выше символьной форме записи выражения для мощности источника э.д.с., стрелочки, поставленные над обозначениями источников э.д.с и тока, протекающего в цепи, сонаправлено, поэтому в кружке записан знак плюс.
Именно это обстоятельство и указывает на то, что источник э.д.с. функционирует в генераторном режиме: в этом режиме источник “отдает” свою энергию в цепь, а на нагрузке происходит преобразование этой электрической энергии в другие ее виды.
Приведем (напомним) определение режима “потребителя” для источника э.д.с. 
Источник э.д.с. функционирует в режиме потребителя, тогда и только тогда, когда величина мощности, им потребляемая и определяемая по соотношению
 меньше нуля.
меньше нуля.
В последней записи выражения для мощности источника э.д.с. стрелочки направлены уже встречно, поэтому в кружке записан знак минус.
Это обстоятельство указывает на то, что источник э.д.с. функционирует в режиме потребителя, такой случай возможен, когда, например, в линейной электрической цепи постоянного тока, имеются два источника э.д.с., но величина одного из них больше величины другого. Такой случай, в дальнейшем изложении, детально нами анализируется и для него будет составлен баланс мощностей.
Выполним анализ режима функционирования рассматриваемой линейной электрической цепи при условии, что при этом выполняется соотношение (1.3.4).
Проводимый анализ основан на применении фундаментального закона природы – закона сохранении энергии и второго закона Кирхгофа, который фактически вытекает из этого фундаментала.
Записывая второй закон Кирхгофа, применительно к рассматриваемой линейной электрической цепи, для анализируемого ее режима, найдем:
|
|
|

Тогда, опираясь на определение мощности, представленное в виде ранее полученного следующего базисного соотношения
 ,
, 
непосредственно находим выражение, определяющее мощность  источника:
источника:


 выражение, определяющее энергию, которую поставляет источник в цепь.
выражение, определяющее энергию, которую поставляет источник в цепь.
В свою очередь, выражение, определяющее энергию,  поглощаемую нагрузкой, можно записать в следующем виде:
поглощаемую нагрузкой, можно записать в следующем виде:

 .
.
Выражение, определяющее  энергию, которая бесполезно теряется, точнее говоря, преобразуется в тепловую энергию, на внутреннем сопротивлении самого источника, примет следующую аналитическую форму записи:
энергию, которая бесполезно теряется, точнее говоря, преобразуется в тепловую энергию, на внутреннем сопротивлении самого источника, примет следующую аналитическую форму записи:


отсюда, непосредственно находим:


Применяя, к рассматриваемой цепи, закон сохранения энергии, находим:


Сопоставляя между собой соотношения (1.3.9) и (1.3.10), делаем вывод: об их несовместимости. Итак, соотношение (1.3.9) противоречит закону сохранения энергии, записанному в виде соотношения (1.3.10), применительно к рассматриваемой линейной электрической цепи.
Покажем, как можно прийти к этому же выводу, рассуждая несколько иначе.
Действительно, используя полученное нами выше соотношение  , запишем следующие аналитические выражения:
, запишем следующие аналитические выражения:
1)  для мощности в нагрузке;
для мощности в нагрузке;
2)  для мощности потерь на внутреннем сопротивлении источника э.д.с.
для мощности потерь на внутреннем сопротивлении источника э.д.с.
Выражение для мощности источника э.д.с., записывается с учетом соотношения (1.1.19), в котором это выражение приведено в самом общем виде, поэтому имеем:
 -первая вариация для мощности, источника э.д.с.; которая записывается с учетом топологии цепи, а вторая ее вариация получается в результате применения закона сохранения энергии к данной цепи:
-первая вариация для мощности, источника э.д.с.; которая записывается с учетом топологии цепи, а вторая ее вариация получается в результате применения закона сохранения энергии к данной цепи:
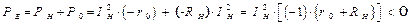 .
.
Сопоставляя между собой эти две вариации, убеждаемся в их несовместимости, т. е., противоречивости. Противоречивость состоит в следующем: первая вариация мощности источника э.д.с. записана для его генераторного режима, в то время как вторая – для его режима, как потребителя. Одновременность этих режимов функционирования источника э.д.с. возможна лишь в режиме КЗ, который нами был рассмотрен ранее.
|
|
|
Отсюда, следует, важный с физической точки зрения, вывод: соотношение  не имеет места в линейных электрических цепях. Оно имеет место в нелинейных электрических цепях, т.е., таких цепях, в которых, не выполняется принцип суперпозиции и не выполняется в общем случае закон Ома. В то же время, законы Кирхгофа выполняются как в линейных, так и нелинейных электрических цепях.
не имеет места в линейных электрических цепях. Оно имеет место в нелинейных электрических цепях, т.е., таких цепях, в которых, не выполняется принцип суперпозиции и не выполняется в общем случае закон Ома. В то же время, законы Кирхгофа выполняются как в линейных, так и нелинейных электрических цепях.
Яркими представителями нелинейных цепей выступают цепи, содержащие туннельные диоды, транзисторы, диоды, стабилитроны и т.п. нелинейные элементы, для которых зависимость между входной физической величиной и выходной величиной, описывается в общем случае нелинейной функцией. В качестве основополагающих портретов нелинейных элементов выступают их внешние характеристики.
Под внешними характеристиками безразлично какого-либо элемента цепи, понимают зависимость тока, протекающего через данный элемент цепи от величины разности потенциалов, приложенной к данному элементу.
Отметим, что при определенных ограничениях, накладываемых с учетом физической сущности рассматриваемого явления, на процесс функционирования данного элемента в конкретной цепи, его внешняя характеристика будет иметь различные аналитические выражения. Кроме этого, необходимо отметить, что существует еще один важный параметр, по которому можно безошибочно определить: какой элемент цепи рассматривается: линейный, либо нелинейный. В качестве такого параметра целесообразно рассматривать дифференциальное сопротивление данного элемента. О физической сущности этого параметра будет подробно изложено в курсе “Электроника“. Здесь же лишь отметим, что у линейных элементов дифференциальное сопротивление – величина постоянная, в то время, как у нелинейных элементов она – переменная.
Соотношение  , полученное выше, характеризует собой режим функционирования цепи, как промежуточный режим - между режимами КЗ и ХХ. Приведем определение данному режиму
, полученное выше, характеризует собой режим функционирования цепи, как промежуточный режим - между режимами КЗ и ХХ. Приведем определение данному режиму  .
.
Определение. Режимом согласованной нагрузки, или согласованным режимом  , называется такой режим функционирования линейной электрической цепи, при котором числовое значение внутреннего сопротивления
, называется такой режим функционирования линейной электрической цепи, при котором числовое значение внутреннего сопротивления  источника ЭДС, численно равно величине
источника ЭДС, численно равно величине  сопротивления нагрузки.
сопротивления нагрузки.
Для последующего анализа необходимо будет определить следующие энергетические характеристики (параметры) цепи для режима согласования  :
:
 .
.
где:
 обозначение мощности источника ЭДС в согласованном режиме
обозначение мощности источника ЭДС в согласованном режиме  ,
, 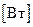 ;
;
 обозначение мощности, выделяющейся на нагрузке в режиме
обозначение мощности, выделяющейся на нагрузке в режиме  ,
,  ;
;
 обозначение мощности, которая выделяется на внутреннем сопротивлении источника Э.Д.С., в режиме
обозначение мощности, которая выделяется на внутреннем сопротивлении источника Э.Д.С., в режиме  ,
, 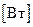 ;
;
|
|
|
 обозначение КПД цепи, в режиме
обозначение КПД цепи, в режиме  ;
;
 обозначение силы тока в режиме
обозначение силы тока в режиме  , [А].
, [А].
Перейдем к определению указанных характеристик (параметров):
1) Аналитическое выражение, определяющее ток в режиме согласования  , имеет следующий вид:
, имеет следующий вид:



2) Запишем аналитическое выражение, определяющее мощность источника ЭДС в режиме согласования  :
:



3) Аналитическое выражение, для  мощности, выделяющейся в нагрузке, в режиме согласования определяется следующим образом:
мощности, выделяющейся в нагрузке, в режиме согласования определяется следующим образом:


 (1.3.13)
(1.3.13)
4) Аналитическое выражение, определяющее  мощность потерь, выделяющуюся на внутреннем сопротивлении
мощность потерь, выделяющуюся на внутреннем сопротивлении  самого источника электродвижущей силы, имеет следующий вид:
самого источника электродвижущей силы, имеет следующий вид:


 (1.3.14)
(1.3.14)
5) Аналитическое выражение, определяющее коэффициент полезного действия  в режиме согласования, имеет следующий вид:
в режиме согласования, имеет следующий вид:
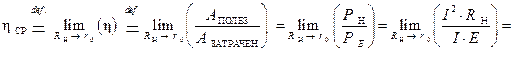




Выполним проверку для режима согласованной нагрузки, опираясь при этом на фундаментальный закон природы – закон сохранении энергии. В силу закона сохранения энергии, с учетом взаимосвязи между энергией и работой, можно записать следующее аналитическое выражение:

Тогда, применяя данный фундаментальный закон природы применительно к анализируемому режиму функционирования рассматриваемой линейной электрической цепи, можем записать:

 .
.
С учетом всего выше сказанного, находим:


 ,
,
что и требовалось доказать.
Прежде, чем приступить к выполнению построения графиков функций, для найденных выше зависимостей, необходимо, провести более детальный анализ режима согласования, используя для этой цели метод исследования функции с помощью производных, подробно изложенный в курсе дифференциального исчисления  .
.
Итак, ранее были получены следующие соотношения:
 (1.1.7);
(1.1.7);  ;
;  ;
;  (1.3.13).
(1.3.13).
Выясним, на каком из участков изменения величины 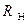 мощность в нагрузке
мощность в нагрузке  , будет увеличиваться, а на каком участке – уменьшаться
, будет увеличиваться, а на каком участке – уменьшаться 
Для однозначного ответа на поставленный вопрос воспользуемся методикой исследования, на экстремумы для интересующей нас функции  , эта методика хорошо известна читателю из курса дифференциального исчисления
, эта методика хорошо известна читателю из курса дифференциального исчисления  .
.
С этой целью, прежде всего, вычисляем производную первого порядка:






Для того чтобы определить критические точки первого рода, необходимо, приравнять полученное выше аналитическое выражение для производной первого порядка к нулю  :
:
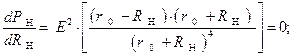
 .
.
После этого соотношение (1.3.19), полученное выше, перепишем в равносильном ему виде, но представленное в виде следующей системы:

 .
.
Нетрудно увидеть, что последняя система, записанная выше, имеет два следующих решения:
 .
.
Второй случай ее решения в данном пособии не рассматривается, в силу того обстоятельства, о котором было сказано ранее.
Ниже, на рис. 2 приводим схему исследования функции  , используя для этой цели
, используя для этой цели  производную первого порядка
производную первого порядка  .
.

Рис. 3. Схема исследования функции 
Дадим краткие пояснения к приведенной выше схеме исследования.
Пусть значение резистора нагрузки удовлетворяет, условию: 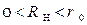 а, именно:
а, именно:  , тогда значение производной при указанном значении аргумента составит
, тогда значение производной при указанном значении аргумента составит  :
:
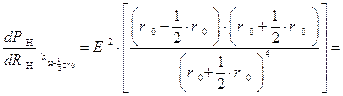

 (1.3.21).
(1.3.21).
Из соотношения (1.3.21) видно, что при значениях переменного резистора нагрузки  больших нуля, но меньших величины внутреннего сопротивления нагрузки, производная первого порядка от функции
больших нуля, но меньших величины внутреннего сопротивления нагрузки, производная первого порядка от функции  положительна, следовательно, сама функция является монотонно возрастающей. Это обстоятельство и отображено соответствующим образом на рис. 2.
положительна, следовательно, сама функция является монотонно возрастающей. Это обстоятельство и отображено соответствующим образом на рис. 2.
Если теперь значение переменного резистора нагрузки составит:  , то тогда значение производной при указанном значении аргумента будет
, то тогда значение производной при указанном значении аргумента будет 
 .
.

 .
.
Из соотношения (1.3.22) видно, что при значениях переменного резистора нагрузки  больших величины внутреннего сопротивления нагрузки, но меньших, чем величина сопротивления нагрузки в режиме ХХ, производная первого порядка, найденная от функции
больших величины внутреннего сопротивления нагрузки, но меньших, чем величина сопротивления нагрузки в режиме ХХ, производная первого порядка, найденная от функции  - отрицательна, следовательно, сама функция является монотонно убывающей на этом интервале. Это обстоятельство и отображено соответствующим образом на рис. 2.
- отрицательна, следовательно, сама функция является монотонно убывающей на этом интервале. Это обстоятельство и отображено соответствующим образом на рис. 2.
В точке со значением 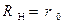 , которая соответствует режиму согласования, значение производной первого порядка равно нулю, в тоже время слева от этой точки производная имеет положительное значение, а справа – отрицательное.
, которая соответствует режиму согласования, значение производной первого порядка равно нулю, в тоже время слева от этой точки производная имеет положительное значение, а справа – отрицательное.
Таким образом, при переходе графика функции  через критическую точку первого рода, в качестве которой выступает величина нагрузки, численно равная
через критическую точку первого рода, в качестве которой выступает величина нагрузки, численно равная  , происходит смена знака у производной с плюса на минус, а это, как известно, из курса дифференциального исчисления, означает лишь то, что в рассматриваемой точке сама функция
, происходит смена знака у производной с плюса на минус, а это, как известно, из курса дифференциального исчисления, означает лишь то, что в рассматриваемой точке сама функция  имеет максимум, поэтому можем записать:
имеет максимум, поэтому можем записать:
 .
.
Вывод:
Режим согласованной нагрузки является наиболее выгодным с энергетической точки: по реальному максимальному значению мощности, передаваемой источником электрической энергии потребителю (приемнику).
Коэффициент полезного действия всей цепи в режиме согласования, как было получено выше, численно равен  .
.
Очередная фаза исследований состоит в построении графиков следующих зависимостей:
1)  ;
;
2)  ;
;
3)  ;
;
4)  ;
;
5)  .
.
Дадим пояснения, необходимые для построения графиков:
Для того чтобы выполнить построение графика зависимости  , необходимо воспользоваться приведенным выше соотношением
, необходимо воспользоваться приведенным выше соотношением
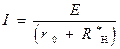
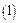 .
.
Из соотношения 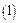 видно, что между током, протекающим через нагрузку, и величиной нагрузки, имеет место квази гиперболическая зависимость.
видно, что между током, протекающим через нагрузку, и величиной нагрузки, имеет место квази гиперболическая зависимость.
При выполнении построения графика зависимости  , необходимо использовать выражение
, необходимо использовать выражение 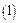 , а также определение “генераторного “ режима, приведенное ранее, в силу этого имеем:
, а также определение “генераторного “ режима, приведенное ранее, в силу этого имеем:
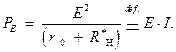

Из формулы (1.3.23) непосредственно следует, что и в этом случае имеет место квази гиперболическая зависимость между мощностью источника (ЭДС) и изменяющейся величиной резистора нагрузки.
При выполнении построения графика функциональной зависимости  , необходимо, использовать следующее выражение:
, необходимо, использовать следующее выражение:


 .
.
Соотношение (1.3.24) представляет собой дробно – рациональную функцию, аналитическое исследование функций, подобных рассматриваемой, подробно изучалось в курсе “ Дифференциальное исчисление“. Отметим здесь лишь то, что в алгоритм исследования функции обязательно входят следующие пункты, которые посвященные нахождению: области определению функции; области изменения функции, нулям функции, четности и нечетности функции, интервалам знака постоянства, определению асимптот, определению критических точек первого и второго рода, а также граничных значений функции.
Некоторые из перечисленных выше пунктов, нами были выполнены ранее, так, в частности, была определена критическая точка первого рода, были определены интервалы знака постоянства. С целью выполнения эскиза функции  , необходимо найти нули и граничные значения функции, а так же критическую точку второго рода.
, необходимо найти нули и граничные значения функции, а так же критическую точку второго рода.
Найдем область  определения функции
определения функции
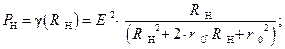 очевидно, что у данной функции в качестве
очевидно, что у данной функции в качестве  области определения выступает объединение двух открытых интервалов
области определения выступает объединение двух открытых интервалов 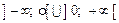 , так что в итоге можно это записать так
, так что в итоге можно это записать так  .
.
Докажем, что функция  непрерывна во всей своей области определения. Для этого первоначально выбираем произвольное значение
непрерывна во всей своей области определения. Для этого первоначально выбираем произвольное значение  из области определения функции, которое обозначим через символ
из области определения функции, которое обозначим через символ  . Тогда, значение функции
. Тогда, значение функции  при выбранном значении аргумента, равного
при выбранном значении аргумента, равного  , будет
, будет
 .
.
Пусть теперь, аргумент рассматриваемой функции, примет новое значение,  где
где  отличное от первоначального, произвольно взятого значения. Очевидно, что новое значение функции составит
отличное от первоначального, произвольно взятого значения. Очевидно, что новое значение функции составит
 .
.
Тогда  приращение функции
приращение функции
 .
.
Выполняя процедуру  предельного перехода для
предельного перехода для  приращения функции, найдем;
приращения функции, найдем; 
 ,
,
что рассматриваемая функция непрерывна.
Анализируя знаменатель  полученной выше дроби, убеждаемся в том, что при любом значении аргумента, взятом из области определения функции
полученной выше дроби, убеждаемся в том, что при любом значении аргумента, взятом из области определения функции  , эта функция не имеет разрывов второго рода, в силу этого у функции не существует вертикальных асимптот.
, эта функция не имеет разрывов второго рода, в силу этого у функции не существует вертикальных асимптот.
Очевидно, что нули функции определяются в результате приравнивания ее числителя нулю. В результате этого найдем:  это и есть нуль функции.
это и есть нуль функции.
Исходя, из физической сущности анализируемой цепи, утверждаем, что функция  имеет одно
имеет одно  граничное значение. В качестве второго квази предельного значения для данной функции выступает граничное значение
граничное значение. В качестве второго квази предельного значения для данной функции выступает граничное значение  .
.
Действительно, как нетрудно видеть, что функция  при условии
при условии  , принимает одну из возможных неопределенностей, указанных нами выше
, принимает одну из возможных неопределенностей, указанных нами выше  :
:

 ,
,
такой вид неопределенностей, как хорошо известно, из курса “Дифференциальное исчисление“, раскрывается, в частности, по правилу И. Бернулли – Лопиталя.
Поэтому, прежде чем переходить к определению граничных значений для функции  , положим в соотношении (1.3.24):
, положим в соотношении (1.3.24):

и тогда, следуя правилу И. Бернулли – Лопиталя, последовательно находим производные первого порядка для введенных  функций:
функций:

После этого, осуществим процедуру предельного перехода в модифицированном соотношении (1.3.24) с целью определения граничного значения функции  , при выполнении следующего условия
, при выполнении следующего условия  :
:

 .
.
Итак, неопределенность вида  , указанная выше, раскрыта.
, указанная выше, раскрыта.
Раскрытая неопределенность позволила определить горизонтальную асимптоту для функции  .
.
Перейдем теперь к вычислению квази предельного значения функции  :
:
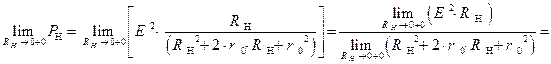
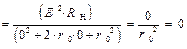 .
.
Учитывая, что одной из основополагающих функций в проводимых исследованиях является  функция мощности, выделяющейся в нагрузке, продолжим исследование этой функции, применяя для этого
функция мощности, выделяющейся в нагрузке, продолжим исследование этой функции, применяя для этого  вторую производную от мощности в нагрузке по величине сопротивления нагрузки, которая позволит определить интервалы выпуклости и вогнутости.
вторую производную от мощности в нагрузке по величине сопротивления нагрузки, которая позволит определить интервалы выпуклости и вогнутости.
Как известно из курса “Дифференциальное исчисление“, критическая точка второго рода находится с помощью производной второго порядка, которую необходимо приравнять к нулю  .
.
Найдем производную второго порядка:




 .
.
Для определения критической точки второго рода, приравниваем числитель полученной выше дроби к нулю, а саму эту дробь записываем в виде системы  .
.
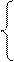

 .
.
Из соотношения  , взятого из системы
, взятого из системы  , находим
, находим  :
:


 .
.
Итак,  - критическая точка второго рода.
- критическая точка второго рода.
Используя критическую точку первого и второго рода, определим интервалы выпуклости и вогнутости функции  .
.
Первоначально принимаем значение величины 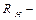 сопротивления нагрузки, равное
сопротивления нагрузки, равное  , т.е., немного меньшее величины согласованной нагрузки, и, выполнив ряд тривиальных преобразований в выражении для второй производной, определим знак этой производной
, т.е., немного меньшее величины согласованной нагрузки, и, выполнив ряд тривиальных преобразований в выражении для второй производной, определим знак этой производной 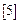
 .
.
Следовательно, при значении величины 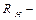 сопротивления нагрузки, принадлежащем открытому интервалу
сопротивления нагрузки, принадлежащем открытому интервалу  , величина второй производной меньше нуля.
, величина второй производной меньше нуля.
Тогда, применяя мнемоническое правило – правило “дождя“, которое широко известно в профессиональных математических кругах 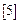 , утверждаем, что на указанном интервале, функция
, утверждаем, что на указанном интервале, функция  будет вогнута вверх, другими словами выпукла.
будет вогнута вверх, другими словами выпукла.
На следующем шаге аналитического исследования функции  , принимаем значение величины
, принимаем значение величины 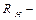 сопротивления нагрузки, т.е., немного большее величины внутреннего сопротивления источника, в рассматриваемом случае это значение берется равное утроенному значению величине нагрузки в режиме согласования
сопротивления нагрузки, т.е., немного большее величины внутреннего сопротивления источника, в рассматриваемом случае это значение берется равное утроенному значению величине нагрузки в режиме согласования 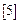
 .
.
После этого, выполняя ряд тривиальных преобразований в выражении для второй производной, определим знак этой производной:
 .
.
В последнем строгом неравенстве было учтено, что величина внутреннего сопротивления источника энергии в рассматриваемой цепи всегда больше нуля, т.е.,  .
.
Применение мнемонического правила – правила “дождя“


