 |
Расчет цепей постоянного тока методом эквивалентного генератора
|
|
|
|
5.1. Исходные положения метода: теорема об активном двухполюснике и закон Ома для обобщенной ветви
В данной лекции рассматривается методология анализа линейной электрической цепи. В теории линейных электрических цепей, как правило, под анализом цепи понимают следующее: задана топология цепи, заданы величины элементов цепи, требуется определить законы токов, протекающих в ветвях – это в общем случае, а в частном - их величины, это же замечание относится и к падениям напряжений на ветвях, составить баланс мощностей.
Электротехническая наука за свою более чем двухсотлетнюю историю развития создала несколько методов, которые широко применяются при анализе линейных цепей. Одним из таких методов является метод эквивалентного генератора.
Данный метод расчёта линейных электрических цепей в учебной литературе имеет и другие названия. Он называется также методом эквивалентного источника, методом активного двухполюсника или методом холостого хода и короткого замыкания. Каждое из этих названий несёт определённую смысловую нагрузку, которая станет понятной по мере его рассмотрения. Следует отметить, что название метода не меняет его физической сущности.
Как нами было сказано выше, при анализе цепей часто приходится определять ток, напряжение и потребляемую мощность в одной из ветвей сложной схемы. Для определе ния этих величин можно выделить эту ветвь из схемы, представив остальную часть схемы активным двухполюсником с двумя выходными зажимами.
Активный двухполюсник, каким бы он ни был сложным по своему внутреннему содержанию, можно заменить на простейший эквивалентный источник электрической энергии, состоящий либо из идеального источника напряжения (ЭДС), либо из идеального источника тока (J), и некоторого сопротивления, находящегося в нутрии этого источника.
|
|
|
Эквивалентные источники должны быть такими, чтобы напряжение или потребляемый ток на их зажимах сохранялись неизменными. Если будут определены параметры такого эквивалентного источника, то тогда ток в рассматриваемой ветви, можно найти следуя закону Ома для обобщенной ветви. Этот метод был предложен выдающимся немецким естествоиспытателем 19 века Германом Гельмгольцем. Возможность замены активной части схемы эквивалентным источником с определением его параметров доказывается в теореме об активном двухполюснике (отсюда следует одно из названий метода)  .
.
Теорема исследована в двух вариантах: когда активный двухполюсник заменяется эквивалентным источником напряжения (это теорема Тевенена) и когда этот источник замещается эквивалентным источником тока (теорема Нортона). Источник напряжения и источник тока могут быть взаимно преобразованы об этом говорилось выше. Поэтому чаще используется один из этих вариантов, в частности, при замене активного двухполюсника эквивалентным источником напряжения, т.е, применяют теорему Тевенена.
5.1.2. Теорема об активном двухполюснике
Рассмотрим первый вариант теоремы.
Активным двухполюсником называют любую электрическую цепь, содержащую источники электроэнергии и два полюса (зажима), к которым, может быть подключен потребитель электрической энергии т. е., нагрузка.
Согласно этой теореме активный двухполюсник может быть заменён эквивалентным источником напряжения, у которого ЭДС равна напряжению на зажимах двухполюсника в отсутствии нагрузки (это режим холостого хода), а внутреннее сопротивление источника - входному сопротивлению относительно этих зажимов.
Теорема доказывается следующим образом.
|
|
|
Активный двухполюсник, изображенный на рис. 16, не изменит своего режима функционирования, если в его цепь включить два источника электродвижущих сил: при этом, величины ЭДС этих источников равны, но направлены они встречно, как это показано на рис. 17. Режим функционирования активного двухполюсника не изменится и в том случае, если эти ЭДС будут равны напряжению холостого хода на его зажимах. Однако при этом можно утверждать, что одна из ЭДС противоположного направления полностью компенсирует напряжение на зажимах двухполюсника и превратит активный двухполюсник в пассивный.

Рис. 16. Условное графическое изображение активного двухполюсника, находящегося в режиме холостого хода.

Рис. 17. Условное графическое изображение активного двухполюсника, находящегося в режиме холостого хода, при этом к одному из зажимов двухполюсника подключены два идеализированных встречно - направленных источника эдс.

Рис. 18. Условное графическое изображение пассивного двухполюсника, находящегося в режиме холостого хода, когда к одному из зажимов двухполюсника подключен идеализированный источник эдс.
Из всего выше сказанного следует, что любой активный двухполюсник может быть замещен в виде комбинации двух элементов цепи: пассивного двухполюсника и источника ЭДС, величина которой равна величине напряжения холостого хода на зажимах активного двухполюсника (рис.18). Пассивный же двухполюсник, как элемент цепи, всегда может быть представлен в виде резистора, величина которого совпадает с величиной входного сопротивления относительно, его входных зажимов.
Процедура определения входного сопротивления активного двухполюсника состоит в следующем: если внутри данного двухполюсника имеются ветви, содержащие идеальные источники электродвижущих сил, то такие источники исключаются посредством их закорачиванию; если же внутри рассматриваемого двухполюсника имеются ветви с идеальными источниками тока, то такие ветви – разрываются.
Если выделенную часть линейной электрической цепи рассматривать как активный двухполюсник, в состав которого входят реальные источники, то тогда при определении входного сопротивления этого двухполюсника сами источники исключаются, но обязательно остаются их внутренние сопротивления.
|
|
|
Наиболее контрастно этот алгоритм можно проиллюстрировать на примере простейшей схемы замещения источника напряжения с внутренним сопротивлением  , представленной выше на рис.12. Из его вольт - амперной характеристики (ВАХ) вида
, представленной выше на рис.12. Из его вольт - амперной характеристики (ВАХ) вида  следует, что при отсутствии тока во внешней цепи
следует, что при отсутствии тока во внешней цепи  напряжение на его зажимах будет равно ЭДС. И наоборот, ЭДС будет равна напряжению холостого хода на его зажимах
напряжение на его зажимах будет равно ЭДС. И наоборот, ЭДС будет равна напряжению холостого хода на его зажимах 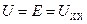 .
.
Если в этой же схеме закоротить зажимы, то тогда при  , предыдущее соотношение принимает следующий
, предыдущее соотношение принимает следующий  , а из него находим, что внутренний ток источника будет равен току короткого замыкания
, а из него находим, что внутренний ток источника будет равен току короткого замыкания
 .
.
Отсюда с учетом того, что выполняется условие

находим выражение для определения внутреннего сопротивления источника:
 .
.
Таким образом, внутреннее сопротивление всегда равно отношению величины напряжения холостого хода, определяемого относительно зажимов источника, к величине тока короткого замыкания. Применительно к рассматриваемой цепи можем утверждать, что величина внутреннего сопротивления источника будет равна величине входного сопротивления, найденного относительно его зажимов, т.е.,  выполняется соотношение:
выполняется соотношение:
 .
.
Итак, рассмотренные параметры  источника электрической энергии, позволяют этот источник уподобить эквивалентного активному двухполюснику. В тоже время сами эти параметры могут быть установлены экспериментально. Вольтметром замеряется напряжение холостого хода, а амперметром - ток короткого замыкания на его зажимах. Это позволяет, выполнив процедуру деления первого результата измерения на второй результат измерения, найти величину входного сопротивления двухполюсника.
источника электрической энергии, позволяют этот источник уподобить эквивалентного активному двухполюснику. В тоже время сами эти параметры могут быть установлены экспериментально. Вольтметром замеряется напряжение холостого хода, а амперметром - ток короткого замыкания на его зажимах. Это позволяет, выполнив процедуру деления первого результата измерения на второй результат измерения, найти величину входного сопротивления двухполюсника.
Если при расчётах методом эквивалентного генератора возникает необходимость использовать эквивалентный источник тока, переход к нему от эквивалентного источника напряжения возможен через их взаимные преобразования без проведения доказательства второго варианта теоремы.
5.1.3. Порядок расчёта (алгоритм) тока в отдельно взятой ветви методом эквивалентного генератора
|
|
|
1.Выделяем ветвь, в которой необходимо рассчитать ток. Остальная часть схемы принимается за активный двухполюсник. Мысленно устраняем (обрываем) ветвь, в которой необходимо определить ток, и после этого рассчитываем величину напряжения на зажимах активного двухполюсника, т.е., находим напряжение холостого хода  на его зажимах, к которым ранее была подключена исключенная ветвь.
на его зажимах, к которым ранее была подключена исключенная ветвь.
2. Определяем напряжение холостого хода  активного двухполюсника на зажимах (узлах, полюсах), к которым была присоединена рассматриваемая ветвь. Это выполняется в следующей последовательности.
активного двухполюсника на зажимах (узлах, полюсах), к которым была присоединена рассматриваемая ветвь. Это выполняется в следующей последовательности.
Первоначально определяются токи в активном двухполюснике - во вновь образованной схеме при отсутствии рассматриваемой ветви. Расчёт этих токов с последующим определением падений напряжений на пассивных элементах преобразованной цепи(одна ветвь исключена нами) проводится любым известным методом. Здесь необходимо сделать одно дополнение относительно выбора метода расчета. Эффективный метод расчета – метод, который обладает наименьшей трудоемкостью, т.е., с математической точки зрения, это метод, который описывается наименьшим числом уравнений  .
.
Затем с помощью алгебраического суммирования падений напряжений на существующих элементах, находящихся в ветвях, вычисляется разность потенциалов в ветвях, расположенных между рассматриваемыми узлами. Эта разность потенциалов и будет являться напряжением холостого хода для активного двухполюсника.
Для правильного решения задачи важно знать не только величину, но и “направление” этого напряжения. Слово направление в предыдущем предложении было заключено в кавычки не просто так. Дело в том, что по своей физической природе напряжение – разность потенциалов, представляет собой скалярную величину, а поэтому, о его направление речь может идти лишь весьма условно.
Для того чтобы указывать условное направление напряжения проводят индексацию узлов цепи. В этой связи узлы обозначают индексами (например, 1 и 2), определив, какой из узлов будет иметь максимальный потенциал, так как
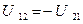 (1.85).
(1.85).
Пусть, например,  .потенциал узла, индекс которого стоит первым, как правило, считается большим в алгебраическом смысле, и напряжение направлено от большего потенциала к меньшему.
.потенциал узла, индекс которого стоит первым, как правило, считается большим в алгебраическом смысле, и напряжение направлено от большего потенциала к меньшему.
Определяем для эквивалентной замены входное сопротивление двухполюсника. Существует два способа, позволяющие определить величину входного сопротивления  . Первый из них выполняется следующим образом.
. Первый из них выполняется следующим образом.
Условно превращаем активный двухполюсник в пассивный: все ЭДС, действующие внутри его, подлежат закорачиванию (если они представляют собой идеальные источники напряжения с нулевыми внутренними сопротивлениями), а все ветви с идельными источниками тока разрываются.
|
|
|
Используя известные правила эквивалентных преобразований для пассивных элементов цепи, в частности для резисторов, ввычисляем входное сопротивление  .
.
Второй способ определения величины входного сопротивления  сводится к следующему.
сводится к следующему.
Любым известным способом определяется величина тока короткого замыкания  при закороченных выходных зажимах активного двухполюсника. Далее, зная значения величин
при закороченных выходных зажимах активного двухполюсника. Далее, зная значения величин  , находим величину входного сопротивления
, находим величину входного сопротивления  по следующему соотношению:
по следующему соотношению:
 (1.86).
(1.86).
После определения основных параметров эквивалентного генератора ( ) схема его приобретает простейший вид (рис. 19). Тогда выражение, служащее для определения тока в выделенной ветви с сопротивлением R, представляет собой закон Ома для обобщенной ветви:
) схема его приобретает простейший вид (рис. 19). Тогда выражение, служащее для определения тока в выделенной ветви с сопротивлением R, представляет собой закон Ома для обобщенной ветви:


Если в ветви, в которой требуется определить ток (рис.19), вместе с резистором R включен идеальный источник электродвижущей силы (ЭДС) 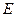 , направление действия которой совпадает с направлением напряжения
, направление действия которой совпадает с направлением напряжения  , то тогда закон Ома для обобщенной ветви принимает другую форму записи:
, то тогда закон Ома для обобщенной ветви принимает другую форму записи:
 (1.88).
(1.88).
Если в разобранном выше случае, ЭДС 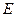 будет включена встречно по отношению к направлению напряжения
будет включена встречно по отношению к направлению напряжения  , то тогда эта ЭДС
, то тогда эта ЭДС 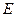 в соотношение (1.88) войдет с отрицательным знаком.
в соотношение (1.88) войдет с отрицательным знаком.

Рис.19 Схема активного двухполюсника, полученная в результате эквивалентных преобразований, совершенных в рассматриваемой цепи (пример 1), и соответствующая теореме Тевенина

Рис.20 Схема активного двухполюсника, полученная в результате эквивалентных преобразований, совершенных в рассматриваемой цепи (пример 1), и соответствующая теореме Нортона
При замене активного двухполюсника эквивалентным источником тока можно принять, что эквивалентный источник тока (рис.20) содержит идеальный источник с током, равным току короткого замыкания  , и параллельно с ним включенный резистор с величиной, равной
, и параллельно с ним включенный резистор с величиной, равной  .
.
При этом ток  распределяется между двумя резисторами,
распределяется между двумя резисторами,  и
и  включенными параллельно. Тогда интересующий нас ток
включенными параллельно. Тогда интересующий нас ток  можно определить следующим образом:
можно определить следующим образом:
 (1.89)
(1.89)
где  .
.
Если в состав выделяемой ветви, кроме резистора с сопротивлением 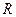 входит еще и
входит еще и  источник ЭДС, направление которой совпадает с направлением тока в этой ветви, то тогда аналитическое выражение для определения величины тока, имеет следующий вид;
источник ЭДС, направление которой совпадает с направлением тока в этой ветви, то тогда аналитическое выражение для определения величины тока, имеет следующий вид;
 (1.90).
(1.90).
Метод эквивалентного генератора чрезвычайно удобен для расчёта тока и напряжений, когда величина сопротивления в исследуемой ветви принимает целый ряд значений (переменное значение). При этом расчёт сводится к анализу простейшей одноконтурной эквивалентной схемы.
5.1.4. Примеры решения задачи основополагающими методами
Метод эквивалентного генератора (МЭГ) с пояснениями
Задача 5.1.4.1
В схеме, представленной на рис.  , определить, следуя методу эквивалентного генератора
, определить, следуя методу эквивалентного генератора  , величину тока в ветви с резистором
, величину тока в ветви с резистором  , если элементы цепи имеют следующие значения:
, если элементы цепи имеют следующие значения:  .
.

Рис. 21. Схема сложной исходной линейной электрической цепи, подлежащая анализу
Решение
Прежде всего, задаемся условными положительными направлениями токов в ветвях, т. е,  .
.
Кроме этого указываем также положительные направления циркуляции контурных токов  , и для тока источника тока
, и для тока источника тока  .
.
Контурные токи в методе эквивалентного генератора (МЭГ) могут быть в ряде случаев, чрезвычайно полезны для определения  величины напряжения холостого хода.
величины напряжения холостого хода.
С целью показать сильные и слабые стороны метода МЭГ, решение данной задачи, будет осуществлено так же и методом контурных токов (МКТ)  .
.
Рассмотрим, первое решение поставленной задачи для этого воспользуемся (МЭГ).
п.1. По условию задачи, необходимо, определить величину тока, протекающего через резистивный элемент  .
.
Для этого размыкаем эту ветвь, после этого всю оставшуюся часть исходной линейной цепи, будем рассматривать в качестве активного двухполюсника, входными зажимами которого выступают теперь не узлы  , а точки
, а точки  . Тогда топология получившейся цепи отобразится в виде следующего рис.22.
. Тогда топология получившейся цепи отобразится в виде следующего рис.22.

Рис. 22 Схема, полученная из исходной цепи, после выполнения преобразования, и подлежащая анализу, по методу эквивалентного генератора (МЭГ)
Из ранее изложенного теоретического материала, следует, что для того чтобы полностью охарактеризовать активный двухполюсник, необходимо, знать его следующие параметры: 1)  входное сопротивление этого двухполюсника и 2)
входное сопротивление этого двухполюсника и 2)  напряжение холостого хода, определяемые относительно зажимом
напряжение холостого хода, определяемые относительно зажимом  .
.
На выше приведенном рисунке  было специально сохранено прежнее направление тока
было специально сохранено прежнее направление тока 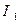 .
.
Схема, позволяющая определить величину  входного сопротивления, приведена на рис.23.
входного сопротивления, приведена на рис.23.

Рис.23. Схема, позволяющая определить величину входного сопротивления активного двухполюсника
Используя схему, приведенную на рис. 23, последовательно находим:
 (1.91)
(1.91)
 (1.92)
(1.92)
После подстановки числовых значений в соотношение (1.92), определяем:


 .
.
Схема, позволяющая определить величину  относительно входных зажимов активного двухполюсника
относительно входных зажимов активного двухполюсника  , приведена ниже на рис. 24.
, приведена ниже на рис. 24.

Рис.24 Схема, позволяющая определить величину напряжения 
Анализ топологии цепи, приведенной выше, позволяет заключить, что эту цепь можно рассчитать, либо по методу узловых потенциалов (МУП), либо по методу контурных токов (МКТ), следствием такого расчета и будет определение величины  .
.
Первоначально выполним расчет этой цепи по (МУП). Этот метод, как буде показано далее, более предпочтителен, так как он менее трудоемкий, в сравнении (МКТ). Важным фактором, выступающим в пользу этого метода, является наличие ветви, содержащей идеальный источник электродвижущей силы ЭДС.
Отметим, между прочим, что основополагающими методами для расчета линейных электрических цепей, являются либо (МУП), либо (МКТ). Алгоритм выбора предпочтения одного из них, в отношении другого, скрыт в самой топологии изначально заданной цепи: если, например, число независимых контуров в исходной цепи, меньше числа ее узлов без одного, то (МКТ) имеет предпочтение перед (МУП), в противном случае, наоборот.
Приняв, 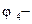 потенциал узла
потенциал узла  , равным нулю, сразу найдем
, равным нулю, сразу найдем  потенциал квази узла
потенциал квази узла 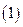 . Действительно, как нетрудно видеть, из приведенного выше рисунка 24, имеют место следующие соотношения:
. Действительно, как нетрудно видеть, из приведенного выше рисунка 24, имеют место следующие соотношения:
 .
.
Итак, остается определить лишь потенциал квази узла  , после чего тривиально находится величина
, после чего тривиально находится величина  .
.
Следуя (МУП), составим следующую систему  уравнений
уравнений 
 |

 .
.
В состав левой части уравнения 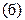 системы
системы  входит известное алгебраическое слагаемое
входит известное алгебраическое слагаемое  и это слагаемое, необходимо перенести в правую часть с противоположным знаком, тогда первоначальная система
и это слагаемое, необходимо перенести в правую часть с противоположным знаком, тогда первоначальная система  , преобразуется в равносильную ей систему, имеющую следующий вид:
, преобразуется в равносильную ей систему, имеющую следующий вид:


 .
.
Следуя методу швейцарского математика Габриеля Крамера  , решим систему
, решим систему  .
.
Прежде всего, запишем аналитическое выражение для  главного определителя системы
главного определителя системы  :
:

 .
.
В соотношение (1.94) элементы определителя – суть проводимости ветвей, берущиеся с надлежащими знаками, как коэффициенты при неизвестных. Неизвестными, как нетрудно видеть, в системе  выступают: как потенциал истинного узла
выступают: как потенциал истинного узла  , так и потенциалы квази узлов
, так и потенциалы квази узлов  .
.
Выполнив процедуру раскрытия  главного определителя второго порядка и осуществив подстановку числовых значений, найдем его числовое значение:
главного определителя второго порядка и осуществив подстановку числовых значений, найдем его числовое значение:



 (1.95).
(1.95).
Итак, 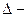 главный определитель системы
главный определитель системы  отличен от нуля, поэтому данная система – совместна, т.е., имеет единственное решение, это утверждение непосредственно следует из элементов теории линейной алгебры
отличен от нуля, поэтому данная система – совместна, т.е., имеет единственное решение, это утверждение непосредственно следует из элементов теории линейной алгебры  .
.
Найдем теперь  первый вспомогательный определитель, получающийся из
первый вспомогательный определитель, получающийся из 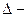 главного определителя системы
главного определителя системы  , с помощью замены элементов его первого столбца – столбцом свободных членов.
, с помощью замены элементов его первого столбца – столбцом свободных членов.
 (1.96).
(1.96).
Выполнив процедуру раскрытия  первого вспомогательного определителя второго порядка и осуществив подстановку числовых значений, найдем его числовое значение:
первого вспомогательного определителя второго порядка и осуществив подстановку числовых значений, найдем его числовое значение:

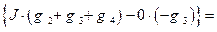

 .
.
Применяя формулу Г. Крамера, найдем:


Выполним проверку размерностей в соотношении (1.98):
 , размерность соблюдается.
, размерность соблюдается.
На следующем шаге находим величину холостого хода  , очевидно, что теперь это не составит большого труда:
, очевидно, что теперь это не составит большого труда:
 (1.99)
(1.99)
Сопоставляя между собой рисунки (21и 22) и используя закон Ома, записанный в обобщенной форме, получаем аналитическое выражение для тока в первой ветви:
 (1.100)
(1.100)
После подстановки числовых значений величин в соотношение (1.99), найдем величину тока 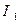
 (1.101).
(1.101).
Итак, задача, изначально поставленная перед нами, решена: величина тока в первой ветви найдена по методу эквивалентного генератора.
Думающий читатель (слушатель), несомненно, поставит перед собой вопрос: как удостоверится в том, что найденное выше значение тока 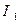 правильное
правильное 
Вопрос этот, надо сказать, по своей физической постановке правильный: в сложной линейной электрической цепи определили лишь один ток из пяти в ней реально имеющихся в качестве неизвестных. Поэтому, для того чтобы положительно ответить на поставленный вопрос о верности значения тока 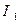 , необходимо и достаточно, следуя (МЭГ) определить еще четыре неизвестных тока, а затем выполнить проверку по первому и второму закону Кирхгофа и осуществить расчет баланса мощностей.
, необходимо и достаточно, следуя (МЭГ) определить еще четыре неизвестных тока, а затем выполнить проверку по первому и второму закону Кирхгофа и осуществить расчет баланса мощностей.
Отсюда следует вывод: по имеющемуся значению одного тока, который протекает в  - той ветви сложной линейной электрической цепи, невозможно однозначно утверждать, что найденное значение верное.
- той ветви сложной линейной электрической цепи, невозможно однозначно утверждать, что найденное значение верное.
Покажем теперь, как можно полностью рассчитать ту же линейную электрическую цепь, представленную на рисунке  , но следуя при этом методу контурных токов (МКТ)
, но следуя при этом методу контурных токов (МКТ)  .
.
Прежде всего, выпишем параметры исходной линейной электрической цепи, под которыми, в частности, в теоретических основах электротехники (ТОЭ), и просто электротехнике, понимают:
1) общее число узлов, обозначаемое через символ  ;
;
2) общее число ветвей, обозначаемое через символ 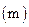 ;
;
3) общее число ветвей, содержащих источники тока  и обозначаемое через символ
и обозначаемое через символ  .
.
Тогда,  число уравнений, которое требуется составить для выполнения расчета рассматриваемой цепи по (МКТ), определяется по следующему соотношению:
число уравнений, которое требуется составить для выполнения расчета рассматриваемой цепи по (МКТ), определяется по следующему соотношению:
 (1.102).
(1.102).
Выпишем значения параметров цепи, схема которой приведена на рис.21:  .
.
Подставив найденные значения указанных параметров в соотношение (1.102), найдем значение  :
:
 (1.103).
(1.103).
Итак, значение параметра  равно двум, оно указывает на то обстоятельство, что существуют два независимых контура в анализируемой цепи.
равно двум, оно указывает на то обстоятельство, что существуют два независимых контура в анализируемой цепи.
Приведем определение независимости контуров.
Два контура, называются независимыми, тогда и только тогда, когда топология одного из них, отличается от топологии другого, хотя бы одной ветвью.
Обозначим эти два независимых контура через условно выбранное положительное направление их обхода, которое удобно задать через последовательность узлов, входящих в данный контур. Тогда первый контур для рассматриваемой цепи можно условно указать в виде следующей последовательности его узлов:  . Эта последовательно
. Эта последовательно  однозначно определяет положительное направление обхода первого контура, которое на рис.(21), обозначено в виде прерывистой стрелки, обтекающей контур против движения стрелки часов. Совершенно аналогично указывается маршрут обхода второго независимого контура в виде последовательности его узлов
однозначно определяет положительное направление обхода первого контура, которое на рис.(21), обозначено в виде прерывистой стрелки, обтекающей контур против движения стрелки часов. Совершенно аналогично указывается маршрут обхода второго независимого контура в виде последовательности его узлов 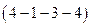 .
.
Из рассмотрения топологии исходной цепи у читателя (слушателя), вероятно, возникает вопрос: как следует понимать контур, занумерованный через следующую последовательность его узлов 
 Дело в том, контуры, содержащие источники тока, безразлично какие – идеальные, либо реальные совсем необычные: в таких контурах не выполняется второй закон Кирхгофа. Такие контуры получили названия квази контуров. Поэтому всегда, произвольно задаваясь положительным направлением обхода контура, содержащего в одной из ветвей хотя бы один источник ЭДС, смотрят за тем, чтобы ветвь с источником тока в такой контур не включалась. Обусловлено это бесконечно большой величиной внутреннего сопротивления
Дело в том, контуры, содержащие источники тока, безразлично какие – идеальные, либо реальные совсем необычные: в таких контурах не выполняется второй закон Кирхгофа. Такие контуры получили названия квази контуров. Поэтому всегда, произвольно задаваясь положительным направлением обхода контура, содержащего в одной из ветвей хотя бы один источник ЭДС, смотрят за тем, чтобы ветвь с источником тока в такой контур не включалась. Обусловлено это бесконечно большой величиной внутреннего сопротивления  идеального источника тока.
идеального источника тока.
Система уравнений, составленная по (МКТ)  , будет иметь следующий вид:
, будет иметь следующий вид:
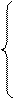 |


Осуществив тривиальное тождественное преобразование в системе  , получим ей равносильную систему
, получим ей равносильную систему  , имеющую вид:
, имеющую вид:
 |


Решение последней системы осуществим по методу Г. Крамера  .
.
Неизвестными в данной системе являются контурные токи  ,
,  , которые необходимо найти. Зная контурные токи, можно найти токи в ветвях: через алгебраическую сумму первых и учитывая при этом определенным образом ток, созданный источником тока.
, которые необходимо найти. Зная контурные токи, можно найти токи в ветвях: через алгебраическую сумму первых и учитывая при этом определенным образом ток, созданный источником тока.
Прежде всего, составим из коэффициентов при неизвестных, выражение для 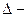 главного определителя этой системы
главного определителя этой системы  :
:

 (1.104).
(1.104).
Выполнив процедуру раскрытия 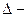 главного определителя второго порядка и осуществив подстановку числовых значений, найдем его числовое значение:
главного определителя второго порядка и осуществив подстановку числовых значений, найдем его числовое значение:
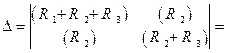

 (1.105).
(1.105).
Размерность  главного определителя системы
главного определителя системы  , как нетрудно видеть, будет:
, как нетрудно видеть, будет:
 .
.
Итак, значение  главного определителя системы
главного определителя системы  отлично от нуля, поэтому в силу сказанного выше, утверждаем, что эта система совместна
отлично от нуля, поэтому в силу сказанного выше, утверждаем, что эта система совместна  .
.
Следуя, вышеуказанному алгоритму, последовательно находим: первый и второй вспомогательный определители, а затем по формуле Крамера – контурные токи.
Cоставляем  первый вспомогательный определитель
первый вспомогательный определитель  :
:
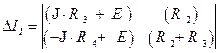 (1.106).
(1.106).
Выполнив процедуру раскрытия этого определителя и подставив числовые значения для элементов, входящих в этот определитель, найдем его значение:


 (1.107).
(1.107).
Тогда, воспользовавшись формулой Крамера, найдем  первый контурный ток:
первый контурный ток:
 (1.108).
(1.108).
Из схемы анализируемой линейной электрической цепи видно, что  ток в первой ветви равен первому контурному току
ток в первой ветви равен первому контурному току  : каждый из этих токов имеет одно направление в первой ветви от узла
: каждый из этих токов имеет одно направление в первой ветви от узла  к узлу
к узлу  , а их числовые значения равны с точностью до знака.
, а их числовые значения равны с точностью до знака.
Cоставляем  второй вспомогательный определитель:
второй вспомогательный определитель: 
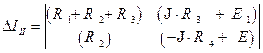 (1.109).
(1.109).
Осуществив процедуру раскрытия этого определителя и подставив числовые значения для элементов, входящих в этот определитель, найдем его значение:


 (1.110).
(1.110).
Затем, воспользовавшись формулой Г. Крамера, находим  второй контурный ток
второй контурный ток  :
:
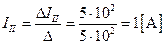 (1.111).
(1.111).
После того, как нашли значения контурных токов  ,
,  , выполняем проверку системы
, выполняем проверку системы  : для этого последовательно подставляем
: для этого последовательно подставляем  значения этих токов в уравнения
значения этих токов в уравнения 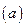 и
и 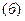 .
.
Тогда, в частности для левой части уравнения  , получим
, получим

 .
.
Аналогично, осуществим проверку уравнения 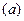 :
:


