 |
Синтез структуры регулятора
|
|
|
|
В структуре управляемого привода два модуля: силовой и управляющий. Управляющий модуль состоит из измерителя рассогласований и регулятора. Для того чтобы система удовлетворяла требованиям технического задания, необходимо провести синтез регулятора.
При помощи правил преобразования структурной схемы, перенесем звено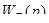 
через первый сумматор, при этом необходимо включить звено 
в обратную связь. Поскольку 
, преобразовав, таким образом, схему, мы получим единичную отрицательную обратную связь. Аналогично перенесем второй сумматор через два звена: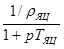 
и 
, добавив эти звенья в локальную обратную связь.
Рис. 2.5. Преобразованная структурная схема привода
Запишем передаточную функцию неизменяемой части системы:
, (2.19)
где 
– коэффициент исходной системы без учета регулятора.
Выражение 2.19 при минимальной и максимальной нагрузках примет следующий вид:
, (2.20)
. (2.21)
Проанализируем устойчивость исходной системы и соответствие системы требованиям по качеству. Об устойчивости системы можно судить по ее реакции на единично ступенчатую функцию, т.е. по ее переходной характеристике. Построим соответствующие графики в программном пакете MATLAB. Графики переходной характеристики представлены на рис. 2.6 – 2.7.
Рис. 2.6. Переходная характеристика исходной системы при минимальной нагрузке на управляемый привод
Рис. 2.7. Переходная характеристика исходной системы при максимальной нагрузке на управляемый привод
Таким образом, мы получили, что исходная система не устойчива. Необходимо введение в исходную систему корректирующего устройства (КУ) для обеспечения требуемого качества как в установившемся (задано в виде динамической ошибки), так и в переходном (ограничения на прямые показатели качества) режимах.
|
|
|
Проведем синтез при помощи метода логарифмических амплитудно-частотных характеристик (ЛАЧХ). Разобьем синтез на условные стадии:
1) Построение ЛАЧХ исходной системы.
2) Построение желаемой ЛАЧХ в соответствие с требованиями ТЗ.
3) Определение передаточной функции КУ.
1) Для построения логарифмических амплитудно-частотных характеристик (ЛАЧХ) неизменяемой части системы проведем расчеты.
. 
Осуществим переход: 
. Тогда выражение для построения ЛАЧХ примет вид:
.
.
.
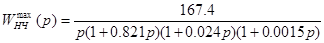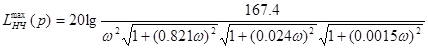2) В ТЗ заданы относительная динамическая ошибка, максимальные скорость и ускорение траектории движения. В соответствие с этим для построения границы запретной области необходимо найти координаты контрольной точки 
.
. (2.22)
. (2.23)
В соответствие с (2.22–2.23) найдем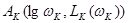 
.
, 
, 
.
Таким образом, 
.
Для того чтобы входное воздействие воспроизводилось с ошибкой, не превосходящей динамическую ошибку, ЛАЧХ системы не должна попадать в запретную область. По рис. 2.8 можно сделать вывод о выполнении требования ТЗ по качеству системы в установившемся режиме, т.к. при минимальном и максимальном значениях электромеханической постоянной двигателя 
ЛАЧХ располагаемой разомкнутой системы не заходит в запретную область. Однако система не удовлетворяет требуемому качеству в переходном режиме 
.
Среднечастотный участок определяет устойчивость и запасы устойчивости системы, а, следовательно, и качество системы в переходном режиме. Для построения среднечастотного участка будем использовать методику Бесекерского [3, с. 369].
Для определения левой и правой границ среднечастотного участка используются неравенства:
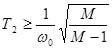, (2.24)
где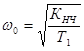 
– базовая частота,
– показатель колебательности.
|
|
|
Значение определим по номограмме [3, c.378]: 
.
Подставим значения в формулу 2.24:
В формулу подставляем значение показателя колебательности: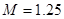 
.
Таким образом, 
,
.
, (2.25)
где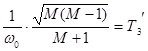 
.
Сначала рассчитаем значение 
и сравним его с постоянными времени исходной системы.
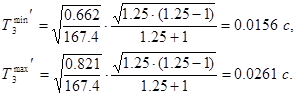
Для вычисления 
необходимо вычесть из 
постоянные времени исходной системы, меньшие чем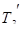 
.
Исходные данные:
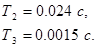
По правилу сначала нужно вычесть наименьшие постоянные времени, поэтому отнимем от 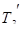только исходной системы:
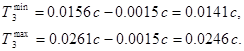
Найдем значение 
из формулы 2.25:
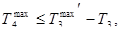
Таким образом, мы рассчитали значения границ среднечастотного участка:
, 
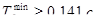Расширяя среднечастотный участок, мы добьемся требуемого качества в переходном режиме. Левую границу будем смещать до тех пор, пока не будет выполняться требуемое значение запаса по модулю 
, которое необходимо выбрать по заданному значению перерегулирования по номограмме [3, с. 358]: 
. Правая граница должна обеспечить запас как минимум 
.
Высокочастотный участок определяет помехозащищенность системы, поэтому наклон высокочастотных асимптот должен быть большим. В то же время с целью упрощения модели корректирующего устройства высокочастотные асимптоты 
выполняют параллельными высокочастотным асимптотам исходной характеристики, то есть на частоте 
наклон становится 80– дБ/дек.
3) Определим передаточную функцию регулятора. Построение представлено на рис. 2.8.
Определим передаточную функцию последовательного КУ:
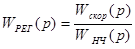. (2.26)
Составим передаточную функцию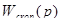 
по виду :
,
.
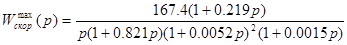По формуле 2.26 найдем 
:
.
|
|
|
