 |
Закон распределения дискретной случайной величины. Многоугольник распределения
|
|
|
|
Случайные величины
Случайная величина. Закон распределения случайной величины
Понятие случайной величины
Одним из важнейших понятий теории вероятностей, наряду со случайным событием и вероятностью, является понятие случайной величины.
Под случайной величиной понимают величину, которая в результате опыта принимает то или иное значение, причем неизвестно заранее, какое именно.
Случайные величины обозначаются прописными латинскими буквами X, Y, Z,... (или строчными греческими буквами 
(кси), 
(эта), 
(тэта) 
(пси) и т.д.), а принимаемые ими значения соответственно малыми буквами х 1, х 2, …, у 1, у 2,…
Примерами случайных величин могут служить: 1) X - число очков, появляющихся при бросании игральной кости; 2) Y - число выстрелов до первого попадания в цель; 3) Z - время безотказной работы прибора, рост человека, курс доллара, количество бракованных деталей в партии, температура воздуха, выигрыш игрока, координата точки при случайном выборе ее на [0; 1], прибыль фирмы, и т.п.
Случайная величина, принимающая конечное или счетное множество значений, называется дискретной.
Если же множество возможных значений случайной величины несчетно, то такая величина называется непрерывной.
То есть дискретная случайная величина принимает отдельные изолированные друг от друга значения, а непрерывная случайная величина может принимать любые значения из некоторого промежутка. Например, значения на отрезке, на всей числовой прямой и. т.д. Отметим, что рассматриваются также случайные величины смешанного типа.
Дадим теперь строгое определение случайной величины, исходя из теоретико-множественной трактовки основных понятий теории вероятностей.
|
|
|
Случайной величиной X называется числовая функция, определенная па пространстве элементарных событий Ω, которая каждому элементарному событию 
ставит в соответствие число 
, т.е. 
, 
(или 
).
Отметим, что если множество Ω конечно или счетно, то случайной величиной является любая функция, определенная на Ω. В общем случае функция должна быть такова, чтобы для любых 
событие 
принадлежало σ-алгебре множеств S и, значит, для любого такого события была определена вероятность 
.
Для полного описания случайной величины недостаточно лишь знания ее возможных значений, необходимо еще знать вероятности этих значений.
Любое правило (таблица, функция, график), позволяющее находить вероятности произвольных событий 
(S - σ-алгебра событий пространства Ω), в частности, указывающее вероятности отдельных значений случайной величины или множества этих значений, называется законом распределения случайной величины (или распределением). Про случайную величину говорят, что «она подчиняется данному закону распределения».
Закон распределения дискретной случайной величины. Многоугольник распределения
Пусть X - дискретная случайная величина, которая принимает значения 
с некоторой вероятностью 
, где 
. Закон распределения дискретной случайной величины удобно задавать с помощью формулы 
, определяющей вероятность того, что в результате опыта случайная величина X примет значение 
. Для дискретной случайной величины X закон распределения может быть задан в виде таблицы распределения:
| X | x 1 | x 2 | … | x n | … |
| P | p 1 | p 2 | … | p n | … |
где первая строкасодержит все возможные значения (обычно в порядке возрастания ) случайной величины,а вторая - их вероятности. Такую таблицу называют рядом распределения.
Так как события 
несовместны и образуют полную группу, то сумма их вероятностей равна единице, т.е. 
.
|
|
|
Закон распределения дискретной случайной величины можно задать графически, если на оси абсцисс отложить возможные значения случайной величины, а на оси ординат - вероятности этих значений. Ломаную, соединяющую последовательно точки (x 1, p 1), (x 2, р 2), … называют многоугольником ( или полигоном ) распределения (см. рис. 5.1).
Рис. 5.1.
Теперь можно дать более точное определение дискретной случайной величины.
Случайная величина X дискретна, если существует конечное или счетное множество чисел таких, что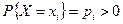 
() и 
.
Определим математические операции над дискретными случайными величинами.
Суммой (разностью, произведением) дискретной случайной величины X, принимающей значения с вероятностями , 
и дискретной случайной величины Y, принимающей значения 
с вероятностями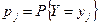 
, 
, называется дискретная случайная величина Z=X+Y (Z=X-Y, Z = X ∙ Y), принимающая значения 
(
, 
) с вероятностями 
для всех указанных значений i и j. В случае совпадения некоторых сумм 
(разностей 
, произведений 
) соответствующие вероятности складываются.
Произведение дискретной случайной величины на число с есть дискретная случайная величина сХ, принимающая значения 
с вероятностями .
Две дискретные случайные величина X и Y называются независимыми, если события 
и 
независимы для любых и , т.е.
.
В противном случае случайные величины называются зависимыми.
Несколько случайных величин называются взаимно независимыми, если закон распределения любой из них не зависит от того, какие возможные значения приняли остальные величины.
Пример 5.1. В урне 8 шаров, из которых 5 белых, остальные - черные. Из нее вынимают наудачу 3 шара. Найти закон распределения числа белых шаров в выборке.
Решение:
Возможные значения случайной величины Х – числа белых шаров в выборке есть 
, 
, 
, 
. Вероятности их соответственно будут
, 
,
, 
.
| 0 | 1 | 2 | 3 |
| 
| 
| 
| 
|
Контроль: 
.
|
|
|
