 |
Биноминальный закон распределения
|
|
|
|
Среди законов распределения дискретной случайной величины наиболее распространенным является биномиальное распределение
Дискретная случайная величина X имеет биномиальное распределение (или распределена по биномиальному закону), если она принимает значения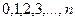 
, с вероятностями:
 ,
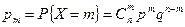| (5.23) |
где 
, 
, 
.
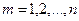Случайная величина X, распределенная по биномиальному закону, является числом успехов с вероятностью р в схеме Бернулли проведения n независимых опытов.
Если требуется вычислить вероятность «не менее m успехов в n независимых опытах», т.е. 
, то имеем:
.
Вероятность 
бывает удобно находить через вероятность противоположного события:
.
Ряд распределения дискретной случайной величины Х, имеющий биномиальное распределение, имеет вид:
| X = m | … | m | … | n | |||
| 
| 
| 
| … | 
| … | 
|
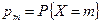
Контроль: 
.
Функция распределения случайной величины Х, распределенная по биномиальному закону имеет вид:
Найдем числовые характеристики этого распределения. Производящей функцией биномиального распределения является:
,
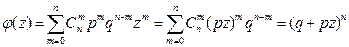т.е. 
. Тогда
,
.
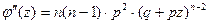Следовательно,
т.к.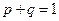 
,
.
Итак,
  .
| (5.24) |
Пример 5.5. Производится 3 независимых выстрела по цели. Вероятности попадания при разных выстрелах одинаковы и равны 
. Найти МХ и DX, где Х – число попаданий в цель.
Решение:
Случайная величина Х имеет биноминальное распределение. Здесь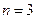 
, , 
. По формулам (5.24) находим МХ и DX:
,
.
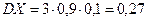Пример 5.6. Составьте таблицу распределения вероятностей числа попаданий в мишень при трех независимых выстрелах, если вероятность попадания при каждом выстреле равна 0,2.
Решение.
Случайная величина X - число попаданий в мишень. Так как производятся три независимых выстрела, то случайная величина может принимать следующие значения:
|
|
|
х 1 = 0, х 2 = 1, х3= 2, х 4=3.
Случайная величина X имеет биномиальное распределение вероятностей, поскольку испытания, рассматриваемые в задаче, удовлетворяют схеме Бернулли. По формуле
,
где m =0,1,2,3, находим:
Р (X =0)=0,512, Р (X =1)=0,384,
Р (X =2)=0,096, Р (X =3)= 0,008.
Таким образом, получаем следующую таблицу распределения вероятностей случайней величины X:
| 0 | 1 | 2 | 3 |
| 0,512 | 0,384 | 0,096 | 0,008 |
Проверка: 
.
Распределение Пуассона
Дискретная случайная величина X имеет распределение Пуассона, если ее возможные значения: 
(счетное множество значений), а соответствующие вероятности выражаются формулой Пуассона
 ,
| (5.25) |
где 
; 
- параметр.
Распределение Пуассона является предельным для биномиального, когда 
и 
так, что 
- постоянно.
Примерами случайных величин, имеющих распределение Пуассона, являются: число вызовов на телефонной станции за время t; число опечаток в большом тексте; число бракованных деталей в большой партии; число 
-частиц, испускаемых радиоактивным источником, и т.д. При этом считается, что события появляются независимо друг от друга с постоянной средней интенсивностью, характеризующейся параметром 
.
Случайная величина X, распределенная по закону Пуассона, имеет следующий ряд распределения
| X = m | … | m | … | |||
| 
| 
| 
| … | 
| … |
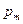
Контроль: 
.
Найдем математическое ожидание и дисперсию случайной величины X, распределенной по закону Пуассона. Производящей функцией распределения Пуассона будет
,
т.е. 
. Тогда
, 
.
Из этого имеем,
,
.
Итак,
 ,
| (5.26) |
т.е. параметр a пуассоновского распределения равен одновременно математическому ожиданию и дисперсии случайной величины X, имеющей это распределение. В этом состоит отличительная особенность изучаемого распределения, которая используется на практике (на основании опытных данных находят оценки для математического ожидания и дисперсии; если они близки между собой, то есть основание считать, что случайная величина распределена по закону Пуассона).
|
|
|
Пример 5.7. Вероятность попадания в цель при одном выстреле равна 0,01. Какова вероятность того, что число попаданий при 200 выстрелах составит не менее 5 и не более 10?
Решение:
Вероятность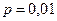 
очень мала, а число выстрелов достаточно велико. Поэтому искомую вероятность будем находить, используя формулу Пуассона. Случайная величина Х – число попаданий. Требуется найти 
.
По теореме сложения вероятностей
.
Имеем:
,
,
.
|
|
|
