 |
Функция распределения и ее свойства. Функция распределения дискретной случайной величины
|
|
|
|
Очевидно, ряд распределения случайной величины может быть построен только для дискретной случайной величины. Для непрерывной случайной величины нельзя даже перечислить все ее возможные значения. Кроме того, вероятность каждого отдельно взятого значения непрерывной случайной величины равна нулю.
Например, вероятность того, что рост мужчины - непрерывная случайная величина - точно равен  метров; купленная нами лампа проработает - непрерывная случайная величина - ровно 900 часов;....
метров; купленная нами лампа проработает - непрерывная случайная величина - ровно 900 часов;....
Как видим, событие возможное, но имеет нулевую вероятность.
Для характеристики поведения непрерывных случайных величин целесообразно использовать вероятность события { X < х }, а не { X=х }), где х - некоторое действительное число. С точки зрения практики нас мало интересует событие, состоящее, например, в том, что лампочка проработает ровно 900 часов, т.е. X = 900. Более важным является событие вида { X <900} (или { X >900}). Такое событие имеет ненулевую вероятность, а при изменении х вероятность события { X <х} в общем случае будет меняться. Следовательно, вероятность Р{ Х < х } является функцией от х.
Универсальным способом задания закона распределения вероятностей, пригодным как для дискретных, так и для непрерывных случайных величин, является ее функция распределения, обозначаемая 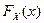 (или просто
(или просто  , без индекса, если ясно, о какой случайной величине идет речь).
, без индекса, если ясно, о какой случайной величине идет речь).
Функцией распределения случайной величины X называется функция  , которая для любого числа
, которая для любого числа  равна вероятности события { Х < х }.
равна вероятности события { Х < х }.
Таким образом, по определению
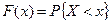 , т.е. , т.е. 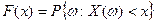 . .
| (5.1) |
Функцию  называют также интегральной функцией распределения. Геометрически равенство (5.1) можно истолковать так:
называют также интегральной функцией распределения. Геометрически равенство (5.1) можно истолковать так:  есть вероятность того, что случайная величина X примет значение, которое изображается на числовой оси точкой, лежащей левее точки х, т.е. случайная точка X попадет в интервал
есть вероятность того, что случайная величина X примет значение, которое изображается на числовой оси точкой, лежащей левее точки х, т.е. случайная точка X попадет в интервал  .
.
|
|
|
Функция распределения обладает следующими свойствами:
1.  ограничена, т.е.
ограничена, т.е.
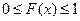 .
.
2.  - неубывающая функция на R, т.е. если
- неубывающая функция на R, т.е. если  , то
, то
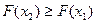 .
.
3.  обращается в нуль на минус бесконечности и равна единице в плюс бесконечности, т.е.
обращается в нуль на минус бесконечности и равна единице в плюс бесконечности, т.е.
 ,
,  .
.
4. Вероятность попадания случайная величина X в промежуток [ а, b) равна приращению ее функции распределения на этом промежутке, т.е.
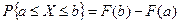 . .
| (5.2) |
5.  непрерывна слева, т.е.
непрерывна слева, т.е.  .
.
Всяка функция  , обладающая свойствами 1-3 и 5, может быть функцией распределения некоторой случайной величины. Формула (5.2) – свойство 4 – справедлива и для непрерывных случайных величин.
, обладающая свойствами 1-3 и 5, может быть функцией распределения некоторой случайной величины. Формула (5.2) – свойство 4 – справедлива и для непрерывных случайных величин.
С помощью функции распределения можно вычислить вероятность события  :
:
 . .
| (5.3) |
Можно дать более точное определение непрерывной случайной величины.
Случайную величину X называют непрерывной, если ее функция распределения непрерывна в любой точке и дифференцируема всюду, кроме, может быть, отдельных точек.
Используя свойство 4 можно показать, что вероятность того, что непрерывная случайная величина X примет заранее указанное определенное значение a, равна нулю.
Действительно, применим формулу (5.2) к промежутку  :
: 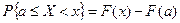 . Будем неограниченно приближать точку х к а. Так как функция
. Будем неограниченно приближать точку х к а. Так как функция  непрерывна в точке а, то
непрерывна в точке а, то 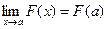 .
.
В пределе получим  . Если функция
. Если функция  везде непрерывна, то вероятность каждого отдельного значения случайной величины равна нулю.
везде непрерывна, то вероятность каждого отдельного значения случайной величины равна нулю.
Следовательно, для непрерывной случайной величины справедливы равенства
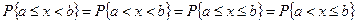
Функция распределения дискретной случайной величины имеет вид
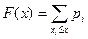 . .
| (5.4) |
Здесь суммирование ведется по всем i, для которых 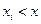 . Равенство (5.4) непосредственно вытекает из определения (5.1).
. Равенство (5.4) непосредственно вытекает из определения (5.1).
Пример 5.2. В урне 8 шаров, из которых 5 белых, остальные - черные. Из нее вынимают наудачу 3 шара. Найти функцию распределения F(x) и построить ее график.
|
|
|
Решение:
Воспользуемся результатами задачи 5.1. Будем задавать различные значения х и находить для них  :
:
1. Если 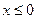 , то
, то 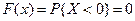 ;
;
2. Если  , то
, то 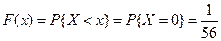 ;
;
3. Если 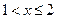 , то
, то  ;
;
4. Если 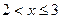 , то
, то  ;
;
5. Если  , то
, то  .
.
Итак,
 . .
| (5.5) |
Отметим, что, пользуясь равенством (5.4), функцию распределения можно сразу записать в виде (5.5)

| 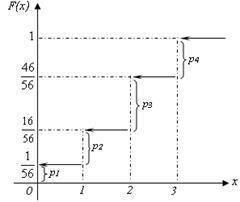 Рис. 5.2.
Рис. 5.2.
|
Как видим (на рис. 5.2), функция распределения дискретной случайной величины Х - разрывная, со скачками рi в точках хi, функция, непрерывная слева: при переходе к точке разрыва слева функция F (x) сохраняет свое значение, ее график имеет ступенчатый вид.
Плотность распределения и ее свойства
Важнейшей характеристикой непрерывной случайной величины, помимо функции распределения, является плотность распределения вероятностей. Напомним, что: случайная величина X называется непрерывной, если ее функция распределения непрерывна и дифференцируема всюду, кроме, быть может, отдельных точек.
Плотностью распределения вероятностей (плотностью распределения, плотностью вероятностей или просто плотностью) непрерывной случайной величины X называется производная ее функции распределения.
Обозначается плотность распределения непрерывной случайной величины X через 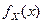 (или
(или 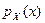 ) или просто
) или просто  (или
(или 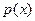 ), если ясно о какой случайной величине идет речь.
), если ясно о какой случайной величине идет речь.
Таким образом, по определению
 . .
| (5.6) |
Функцию  называют также дифференциальной функцией распределения. Она является одной из форм закона распределения случайной величины, существует только для непрерывных случайных величин.
называют также дифференциальной функцией распределения. Она является одной из форм закона распределения случайной величины, существует только для непрерывных случайных величин.
Установим вероятностный смысл плотности распределения. Из определения производной следует
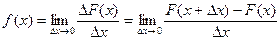
Но согласно формуле (5.2),  .
.
Отношение 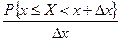 представляет собой среднюю вероятность, которая приходится на единицу длины участка
представляет собой среднюю вероятность, которая приходится на единицу длины участка 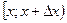 , т.е. среднюю плотность распределения вероятности. Тогда
, т.е. среднюю плотность распределения вероятности. Тогда
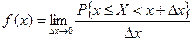 , ,
| (5.7) |
т.е. плотность распределения есть предел отношения вероятности попадания случайной величины в промежуток 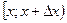 к длине ∆ х этого промежутка, когда ∆ х стремится к нулю. Из равенства (5.7) следует, что
к длине ∆ х этого промежутка, когда ∆ х стремится к нулю. Из равенства (5.7) следует, что
 .
.
То есть плотность вероятности определяется как функция  , удовлетворяющая условию
, удовлетворяющая условию  , выражение
, выражение  называется элементом вероятности.
называется элементом вероятности.
Отметим, что плотность  аналогична таким понятиям, как плотность распределения масс на оси абсцисс или плотность тока в теории электричества.
аналогична таким понятиям, как плотность распределения масс на оси абсцисс или плотность тока в теории электричества.
|
|
|
Плотность распределения обладает следующими свойствами:
1.  неотрицательная т.е.
неотрицательная т.е.
 .
.
2. Вероятность попадания непрерывной случайной величины в промежуток [ a, b ] равна определенному интегралу от ее плотности в пределах от а до b, т.е.
 . .
| (5.8) |
Геометрически эта вероятность равна площади S фигуры, ограниченной сверху кривой распределения  и опирающейся на отрезок
и опирающейся на отрезок  (рис. 5.3). График плотности
(рис. 5.3). График плотности  называют кривой распределения.
называют кривой распределения.

Рис. 5.3.
3. Функция распределения непрерывной случайной величины может быть выражена через ее плотность вероятности по формуле
 .
.
4. Условие нормировки: несобственный интеграл от плотности вероятности непрерывной случайной величины в бесконечных пределах равен единице, т.е.
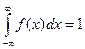 .
.
Геометрически свойство нормировки означает, что площадь фигуры, ограниченной кривой распределения  и осью абсцисс, равна единице.
и осью абсцисс, равна единице.
Пример 5.3. Плотность распределения случайной величины Х задана функцией  . Найти значение параметра а.
. Найти значение параметра а.
Решение:
Согласно свойству 4 плотности, имеем  , тогда
, тогда  , т.е.
, т.е.  или
или  и, наконец, получаем
и, наконец, получаем  , т.е.
, т.е.  .
.
|
|
|


